회원 10명 중에서 회장 1명을 뽑는 경우의 수는 10가지이다. 회장을 뽑은 후 부회장을 뽑는 경우의 수는 회장으로 뽑힌 사람을 제외해야 하므로 9가지이다. 따라서 회장 1명과 부회장 1명을 뽑는 전체 경우의 수는 10 × 9 = 90 이다. 이를 10명 중 2명을 순서를 생각하여 선택하는 순열이라 부르고 \({}_{10} P_{2} \)로 표시한다. <그림 1.1>의 윗부분이 90가지 경우의 수를 보여준다.

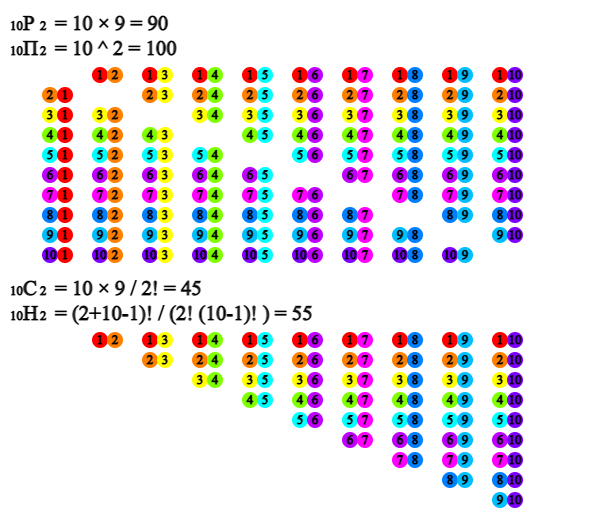
단지 대표 2명을 뽑는 것은 위의 경우에서 회장과 부회장으로 뽑힌 두 사람의 직책을 구분하지 않는 경우로 볼 수 있어 전체 경우의 수는 \(\frac{{}_{10} P_{2}}{2}\) = 45 이다. 이를 10명 중 2명을 순서를 생각하지 않고 선택하는 조합으로 부르고 \({}_{10} C_{2}\)로 표시한다. <그림 1.1>의 아래 부분이 45가지 경우의 수를 보여준다.

10명을 모두 나열하는 경우의 수는 다음과 같고 이를 10! (10 팩토리얼로 읽음)로 표시한다.

일반적으로 \(n\)개의 사물 중 \(r\)개를 선택해 순서를 고려해 나열하는 순열은 다음과 같이 계산된다. .

그러므로 \(n\)개를 모두 나열하는 방법의 수는 다음과 같다.

일반적으로 \(n\)개의 사물 중 \(r\)개를 순서를 고려치 않고 선택하는 경우의 수를 조합이라 하고 다음과 같이 계산된다.

순열과 조합을 수작업이나 계산기를 이용하여 계산하려면 쉽지 않은데 『eStatH』를 이용하면 간편히 계산할 수 있다.

여러 가지 변형된 순열의 경우의 수에 대해 알아보자

10명을 일렬로 배열한 다음의 경우를 생각해 보자

원형 식탁에 않는 경우는 위의 10가지가 모두 같은 경우가 된다. 모든 10! 경우의 수에 위의 경우처럼 10가지씩 같은 경우가 생긴다. 따리서 10명의 회원이 원형 식탁에 둘러않는 경우의 수는

이다. 이와 같이 서로 다른 것을 원형으로 배열하는 순열을 원순열이라 한다.

세 개의 숫자를 이용하여 비밀번호를 정하는 경우의 수는 첫 번째, 두 번째, 세 번째 각 자리의 숫자가 10개씩 있으므로 다음과 같다.

이와 같이 서로 다른 \(n\)개의 사물에서 중복을 허락하여 \(r\)개를 선택하는 순열을 중복순열이라 하고, 기호로 \({}_n \pi_{r}\) 로 표시한다. 중복순열의 수는 \(n\)개의 사물이 첫 번째, 두 번째, ... ,\(r\)번째 자리에 중복해서 나타날 수 있으므로 다음과 같다.

세 개의 검은 공을 B, B, B 두 개의 빨간 공을 R, R로 표시하자. 각각의 공이 모두 다르다면 120개의 서로 다른 공의 순열이 생긴다. 하지만 검은 공 세 개와 빨간 공 두 개가 서로 같으므로 120개의 순열 중 구별할 수 없는 경우가 생긴다. 예를 들어, 검은 공을 \(B_1 \), \(B_2 \), \(B_3 \) 빨간 공을 \(R_1 \), \(R_2 \)로 표시하여 순열을 생각하면 다음과 같은 12가지의 순열은 모두 동일한 B, B, B, R, R 이라는 순열이다.

검은 공을 \(B_1 , B_2 , B_3 \) 빨간 공을 \(R_1 , R_2 \)로 표시한 순열	검은 공을 B, B, B 빨간 공을 R, R로 표시한 순열
\(B_1 , B_2 , B_3 , R_1 , R_2 \) \(B_1 , B_3 , B_2 , R_1 , R_2 \) \(B_2 , B_1 , B_3 , R_1 , R_2 \) \(B_2 , B_3 , B_1 , R_1 , R_2 \) \(B_3 , B_1 , B_2 , R_1 , R_2 \) \(B_3 , B_2 , B_1 , R_1 , R_2 \) \(B_1 , B_2 , B_3 , R_2 , R_1 \) \(B_1 , B_3 , B_2 , R_2 , R_1 \) \(B_2 , B_1 , B_3 , R_2 , R_1 \) \(B_2 , B_3 , B_1 , R_2 , R_1 \) \(B_3 , B_1 , B_2 , R_2 , R_1 \) \(B_3 , B_2 , B_1 , R_2 , R_1 \)	\(B, B, B, R, R\)

여기서 12가지 경우란 검은 공 세 개의 순열 3! 과 빨간 공 두 개의 순열 2!을 곱한 것이다. 위와 같이 공 5개의 120가지의 순열에는 12가지씩 같은 것이 생기므로 3개의 검정색 공과 2개의 빨간색 공을 일렬로 배열하는 순열의 수는 다음과 같다.

일반적으로 같은 것이 있는 순열은 다음과 같다.

세 가지 색의 연필에서 네 개를 고르려면 중복이 허락되어야 하고, 또 연필을 구입하는 것은 순서를 고려하지 않으므로 조합이다. 이와 같이 중복을 허용하여 만든 조합을 중복조합이라고 한다. 서로 다른 \(n\)개의 사물에서 \(r\)개를 선택하는 중복조합의 수를 \({}_n H_{r}\)로 표시한다.

빨강, 초록, 파랑색 연필을 각각 R, G, B라고 하자. 네 개의 연필을 구입하는 \({}_3 H_{4}\) 경우의 수는 15가지로 다음표의 왼쪽과 같이 적을 수 있다. 여기에 R, G, B를 구분하는 사각형 󰌡을 삽입하면 오른쪽과 같다.

빨강 연필의 개수로 정리한 경우의 수	빨강, 초록, 파랑의 구분선 󰌡을 삽입한 경우의 수
네 개 빨강 R R R R 세 개 빨강 R R R G 세 개 빨강 R R R B 두 개 빨강 R R B B 두 개 빨강 R R G B 두 개 빨강 R R G G 한 개 빨강 R G G G 한 개 빨강 R G G B 한 개 빨강 R G B B 한 개 빨강 R B B B 영 개 빨강 G G G G 영 개 빨강 G G G B 영 개 빨강 G G B B 영 개 빨강 G B B B 영 개 빨강 B B B B	네 개 빨강 R R R R 󰌡 󰌡 세 개 빨강 R R R 󰌡 G 󰌡 세 개 빨강 R R R 󰌡 󰌡 B 두 개 빨강 R R 󰌡 󰌡 B B 두 개 빨강 R R 󰌡 G 󰌡 B 두 개 빨강 R R 󰌡 G G 󰌡 한 개 빨강 R 󰌡 G G G 󰌡 한 개 빨강 R 󰌡 G G 󰌡 B 한 개 빨강 R 󰌡 G 󰌡 B B 한 개 빨강 R 󰌡 󰌡 B B B 영 개 빨강 󰌡 G G G G 󰌡 영 개 빨강 󰌡 G G G 󰌡 B 영 개 빨강 󰌡 G G 󰌡 B B 영 개 빨강 󰌡 G 󰌡 B B B 영 개 빨강 󰌡 󰌡 B B B B

이와 같이 생각하면 서로 다른 세 가지 색의 연필이 있을 때 네 개를 선택하는 중복조합의 수 는 6개의 사물이 있을 때 이 중 같은 것이 네 개 (●,●,●,●), 두 개(󰌡, 󰌡)있는 순열의 수와 같다. 즉

일반적으로 중복조합의 수 \({}_n H_{r}\)는 \(r\)개의 ●와 경계를 구분하는 (\(n-1\))개의 󰌡를 배열하는 같은 것이 있는 순열의 수와 같으므로 다음과 같다.

세 개의 주머니에서 하나씩 구슬을 뽑는 전체 경우의 수와 각 경우에 적힌 문자를 곱했을 때 나타나는 항이 다음과 같다.

세 주머니에서 하나씩 구슬을 뽑는 전체 경우와 적힌 문자의 곱	정리된 문자의 곱	같은 항의 수
은 은 은 ⇨ \(a × a × a\)	\(a^3\)	\({}_3 C_0 = 1\)
은 은 금 ⇨ \(a × a × a\) 은 금 은 ⇨ \(a × b × a\) 금 은 은 ⇨ \(b × a × a\)	\(a^2 b\)	\({}_3 C_1 = 3\)
은 금 금 ⇨ \(a × b × b\) 금 은 금 ⇨ \(b × a × b\) 금 금 은 ⇨ \(b × b × a\)	\(a b^2\)	\({}_3 C_1 = 3\)
금 금 금 ⇨ \(b × b × b\)	\(b^3\)	\({}_3 C_3 = 1\)

이 중에서 \(ab^2 \)가 되는 경우의 수는 세 가지({은,금,금}, {금,은,금}, {금,금,은})로서 세 주머니에서 금구슬을 두 번 뽑는 조합의 수인 \({}_3 C_{2}\) = 3 과 같다.

마찬가지로 항 \(a^3 ,\; a^2 b,\; b^3 \)의 경우의 수는 \({}_3 C_{0} ,\; {}_3 C_{1} ,\; {}_3 C_{3} \)가 된다.

위의 실험은 다항식 \((a+b)^3\)을 전개할 때 나타나는 항과 동일하다 $$ \begin{align} (a+b)^3 ~&=~(a+b)(a+b)(a+b) \\ ~&=~(aa + ab+ba+bb)((a+b) \\ ~&=~aaa+aab+aba+abb+baa+bab+bba+bbb \\ ~&=~a^3 +3a^2 b+3ab^2 +b^3 \end{align} $$ 각 항의 경우의 수를 조합을 이용하여 나타내면 다음과 같다. $$ \begin{align} (a+b)^3 ~=~{}_3 C_{0}a^3 +{}_3 C_{1}a^2 b + {}_3 C_{2}ab^2 + {}_3 C_{3}b^3 \end{align} $$ 일반적으로 \((a+b)^3\)의 전개식은 \(n\)개의 \((a+b)\) 중에서 각각 \(a\) 또는 \(b\)를 하나씩 택하여 곱한 항을 모두 더한 것이다. 여기서 항 \(a^{n-r} b^r\)은 \(n-r\)개에서 각각 \(a\)를 택하고 \(r\)개에서 각각 \(b\)를 택하여 곱한 것이므로 \(a^{n-r} b^r\)의 계수는 \({}_n C_r\)과 같다. 따라서 \((a+b)^n\)의 전개식을 조합의 수를 이용하여 나타내면 다음과 같다. $$ \begin{align} (a+b)^n ~=~{}_n C_{0}a^n +{}_n C_{1}a^{n-1} b + \cdots + {}_n C_{r}a^{n-r}b^r + \cdots + {}_n C_{n}b^n \end{align} $$ 이것을 이항정리라고 하고 각 항의 계수 $$ \begin{align} {}_n C_{0} , {}_n C_{1} , \cdots , {}_n C_{r} , \cdots . {}_n C_{n} \end{align} $$ 을 이항계수라 하고 \({}_n C_{r}a^{n-r}b^r \)를 전개식의 일반항이라고 한다.

\((a+b)^n\)의 이항계수를 각 \(n\)=1,2,3, ... 에 대해 <그림 1.6>과 같이 삼각형 형태로 배열한 것을 파스칼의 삼각형이라고 한다.

파스칼의 삼각형에서 각 단계의 배열은 대칭이다. 이는 두 항 \(a^{n-r}b^r \)과 \(a^{r}b^{n-r} \)의 계수 \({}_n C_{r}\)과 \({}_n C_{n-r}\)이 같기 때문이다.

또 각 단계에서 이웃하는 두 수의 합은 그 다음 단계에서 두수의 중앙에 있는 수와 같음을 알 수 있는데 이는 \({}_n C_{r} = {}_{n-1} C_{r-1} + {}_{n-1} C_{r}\)이기 때문이다.