In our daily life, there are many situations in which we need to make appropriate decisions. In order to make a rational decision, it is necessary to identify possible cases and analyze various alternatives. Observed data often have certain types and rules. In this case, permutation and combination are often used to identify all possible cases.
There are 10 cases in which one chairperson is selected from 10 members. There are nine cases in which the vice-chairperson is elected after selecting the chairperson because the person elected as the chairperson must be excluded. Therefore, the total number of cases in which one chairperson and one vice-chairperson are selected is 10 × 9 = 90. This is called the permutation in which two out of 10 members are selected by considering the order and it is denoted by \({}_{10} P_{2} \). The upper part of <Figure 1.1> shows all cases of 90.
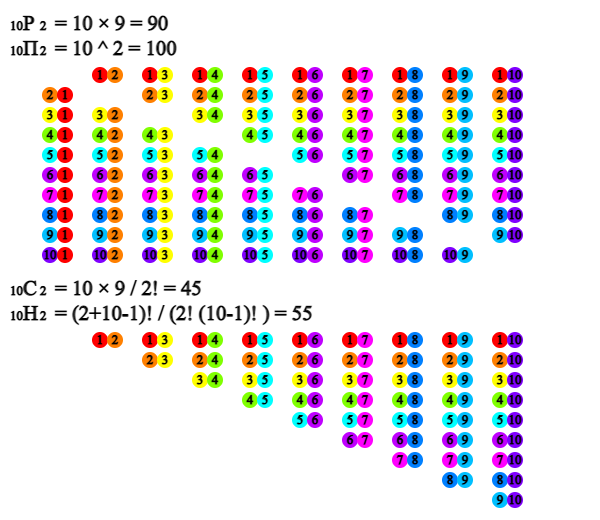
The selection of two officers can be seen as a case where the positions of the two elected chairperson and vice-chairperson are not distinguished in the above cases, so the total number of cases is \(\frac{{}_{10} P_{2}}{2}\) = 45. This is called the combination in which two out of 10 members are selected without considering the order and it is denoted by \({}_{10} C_{2}\). The lower part of <Figure 1.1> shows the number of 45 cases.
The number of cases where all 10 members are listed by considering order is as follows, and it is denoted as 10! (read as 10 factorial).
✨ Permutation
The number of cases which selects \(r\) objects out of \(n\) objects in consideration of the order is calculated as follows:
✨ Combination
The number of cases which selects \(r\) objects out of \(n\) objects without consideration of the order is calculated as follows:
It is not easy to calculate the permutation and combination manually or using a calculator, but 『eStatH』 makes it easy to calculate..
In 『eStatH』 'Permutation Combination' menu, enter \(n\) = 10 and \(r\) = 2, then permutation and combination are calculated immediately.
When \(n\) is less than 10 and \(r\) is equal to 2, if you click [Execute] button, a figure of the number of all cases is displayed such as in <Figure 1.1>.
[Permutation and Combination]
Let us look at the number of cases in various permutations.
Consider the following 10 cases when we list 10 cyclists in a row.
In the case of sitting around a round table, the above 10 cases are all the same. As in the case above, there are 10 cases which are the same if they are sitting around a round table. Therefore, the number of cases where 10 members are sitting around the round table is as follows:
A permutation in which different objects are arranged in a circle in this way is called the circular permutation.
✨ Circular Permutation
A permutation in which \(n\) different objects are arranged in a circle is called the circular permutation and the number of cases is as follows:
Since there are 10 numbers in each of the first, second and third rolls, the number of cases in which a password is set using three rolls is as follows:
A permutation of selecting \(r\) objects by allowing duplicates in \(n\) different objects is called the permutation with replacement, and is denoted by \({}_n \pi_{r}\). Since the number of \(n\) objects can appear repeatedly in the first, second, ... , \(r^{th}\) position, the number of cases is as follows:
✨ Permutation with replacement
A permutation of selecting \(r\) objects by allowing duplicates in \(n\) different objects is as follows:
[Permutation and Combination]
Let's mark the three black balls as B, B, B and the two red balls as R and R. If each ball is different, there are 120 different permutations of the balls. However, since the three black balls and the two red balls are the same, there are indistinguishable cases among 120 permutations. For example, if you consider the permutation of a black ball as \(B_1 \), \(B_2 \), \(B_3 \) and a red ball as \(R_1 \), \(R_2 \) then the following 12 cases are all the same cases of B, B, B, R, R.
| Permutation marked with \(B_1 , B_2 , B_3 \) for black balls \(R_1 , R_2 \) for red balls | Permutation marked with B, B, B for black balls and R, R for red balls |
|---|---|
|
\(B_1 , B_2 , B_3 , R_1 , R_2 \) \(B_1 , B_3 , B_2 , R_1 , R_2 \) \(B_2 , B_1 , B_3 , R_1 , R_2 \) \(B_2 , B_3 , B_1 , R_1 , R_2 \) \(B_3 , B_1 , B_2 , R_1 , R_2 \) \(B_3 , B_2 , B_1 , R_1 , R_2 \) \(B_1 , B_2 , B_3 , R_2 , R_1 \) \(B_1 , B_3 , B_2 , R_2 , R_1 \) \(B_2 , B_1 , B_3 , R_2 , R_1 \) \(B_2 , B_3 , B_1 , R_2 , R_1 \) \(B_3 , B_1 , B_2 , R_2 , R_1 \) \(B_3 , B_2 , B_1 , R_2 , R_1 \) |
\(B, B, B, R, R\) |
The 12 cases here are multiplication of the permutation of three black balls, 3!, with the permutation of two red balls, 2!. As above, in 120 cases of 5 balls permutation, there are 12 identical ones, so the number of permutations arranging 3 black balls and 2 red balls in a row is as follows:
In general, the number of permutations with the same objects are as follow.
✨ Permutation with the same objects
The number of cases to arrange \(n\) objects when there are the same \(p\) objects, \(q\) objects, ... , \(z\) objects is as follows:
[Permutation and Combination]
What is the number of cases to buy four pencils?
In order to choose four from three colored pencils, duplicates must be allowed, and purchasing four pencils is a combination because the order is not considered. A combination by allowing duplicates in this way is called the combination with replacement. The combination with duplicates which selects \(r\) objects from \(n\) different objects is denoted by \({}_n H_{r}\).
Let the red, green, and blue pencils be R, G and B respectively. There are 15 cases of purchasing four pencils as shown on the left of the following table. Inserting a dividing bar ▭ separating R, G and B here is shown on the right.
| Number of cases organized by the number of red pencils | Number of cases in which red, green, blue and dividing bar ▭ are inserted |
|---|---|
|
Four reds R R R R Three reds R R R G Three reds R R R B Two reds R R B B Two reds R R G B Two reds R R G G One red R G G G One red R G G B One red R G B B One red R B B B No red G G G G No red G G G B No red G G B B No red G B B B No red B B B B |
Four reds R R R R ▭ ▭ Three reds R R R ▭ G ▭ Three reds R R R ▭ ▭ B Two reds R R ▭ ▭ B B Two reds R R ▭ G ▭ B Two reds R R ▭ G G ▭ One red R ▭ G G G ▭ One red R ▭ G G ▭ B One red R ▭ G ▭ B B One red R ▭ ▭ B B B No red ▭ G G G G ▭ No red ▭ G G G ▭ B No red ▭ G G ▭ B B No red ▭ G ▭ B B B No red ▭ ▭ B B B B |
Thinking in this way, when there are three different colored pencils, the number of combinations with duplicates \({}_3 H_{4}\) is the same as the number of permutations with four same objects (●,●,●,●) and two same objects (▭, ▭).
In general, the number of combinations with duplicates \({}_n H_{r}\) is equal to the number of permutations with arranging \(r\) number of objects ● and the (\(n-1\)) number of objects ▭ that separates the boundary, so it is as follows:
✨ Combination with replacement
The number of combinations of selecting \(r\) objects from \(n\) different objects is as follows:
[Permutation and Combination]
The total number of cases in which a bead is drawn from three pockets and the terms by multiplying the character written on the bead is as follows:
| Total number of cases in which a bead is drawn from three pockets and the terms by multiplying the character written on the bead | Organized characters | Number of the same characters |
|---|---|---|
| Silver Silver Silver ⇨ \(a × a × a\) | \(a^3\) | \({}_3 C_0 = 1\) |
|
Silver Silver Gold ⇨ \(a × a × a\) Silver Gold Silver ⇨ \(a × b × a\) Gold Silver Silver ⇨ \(b × a × a\) |
\(a^2 b\) | \({}_3 C_1 = 3\) |
|
Silver Gold Gold ⇨ \(a × b × b\) Gold Silver Gold ⇨ \(b × a × b\) Gold Gold Silver ⇨ \(b × b × a\) |
\(a b^2\) | \({}_3 C_1 = 3\) |
| Gold Gold Gold ⇨ \(b × b × b\) | \(b^3\) | \({}_3 C_3 = 1\) |
Among these, there are three cases of \(ab^2 \), ({Silver, Gold, Gold}, {Gold, Silver, Gold}, {Gold, Gold, Silver}), which is the number of combinations of drawing gold beads twice from three pockets \({}_3 C_{2}\) = 3.
Similarly, the number of cases for terms \(a^3\), \(a^2 b\), \(b^3\) becomes \({}_3 C_{0}\), \({}_3 C_{1}\), \({}_3 C_{3}\).
The above experiment is the same as the term appears when the polynomial \((a+b)^3\) is developed.
$$ \begin{align} (a+b)^3 ~&=~(a+b)(a+b)(a+b) \\ ~&=~(aa + ab+ba+bb)((a+b) \\ ~&=~aaa+aab+aba+abb+baa+bab+bba+bbb \\ ~&=~a^3 +3a^2 b+3ab^2 +b^3 \end{align} $$ If the number of cases in each term is expressed using a combination, it is as follows: $$ \begin{align} (a+b)^3 ~=~{}_3 C_{0}a^3 +{}_3 C_{1}a^2 b + {}_3 C_{2}ab^2 + {}_3 C_{3}b^3 \end{align} $$ In general, the expansion of \((a+b)^3\) is the sum of all the multiplication terms by taking each \(a\) or \(b\) from one of \(n\) number of \((a+b)\).
Here, the coefficient of \(a^{n-r} b^r\) is equal to the multiplication of \(a\) from \(n-r\) number of \(a+b\) with \(b\) from \(r\) number of \(a+b\). The coefficient of \(a^{n-r} b^r\) is \({}_n C_r\). Therefore, the expansion of \((a+b)^n\) is expressed using the number of combinations is as follows: $$ \begin{align} (a+b)^n ~=~{}_n C_{0}a^n +{}_n C_{1}a^{n-1} b + \cdots + {}_n C_{r}a^{n-r}b^r + \cdots + {}_n C_{n}b^n \end{align} $$ It is called the binomial theorem, and the coefficient of each term $$ \begin{align} {}_n C_{0} , {}_n C_{1} , \cdots , {}_n C_{r} , \cdots . {}_n C_{n} \end{align} $$ is called the binomial coefficient. The term \({}_n C_{r}a^{n-r}b^r \) is called the general term of the binomial theorem.
✨ Binomial Theorem
Suppose \(n\) is a natural number. $$ \begin{align} (a+b)^n ~=~{}_n C_{0}a^n +{}_n C_{1}a^{n-1} b + \cdots + {}_n C_{r}a^{n-r}b^r + \cdots + {}_n C_{n}b^n \end{align} $$
An arrangement of the binomial coefficients of \((a+b)^n\) when \(n\) = 1, 2, 3. ... in the form of a triangle as shown in <Figure 1.6> is called the Pascal's triangle.
The arrangement of each step in the Pascal's triangle is symmetric. This is because the coefficients of the two terms \(a^{n-r}b^r \) and \(a^{r}b^{n-r} \) which are \({}_n C_{r}\) and \({}_n C_{n-r}\) have the same value.
Also, it can be seen that the sum of two neighboring numbers in each step is equal to the number in the middle of the two numbers in the next step, because \({}_n C_{r} = {}_{n-1} C_{r-1} + {}_{n-1} C_{r}\).
In 『eStatH』 'Binomial Theorem – Pascal's Triangle', enter \(n\) = 8 and click [Execute] to see the result as shown in <Figure 1.6>.
[Pascal Triangle]