Chapter 3. Data summary and transformation
[presentation] [book]
- 3.1 Categorical data summary using tables
- 3.1.1 Frequency table for a single variable
- 3.1.2 Two-dimensional frequency table for two variables
- 3.1.3 Multi-dimensional frequency table for several variables
- 3.2 Quantitative data summary using measures
- 3.2.1 Measures for a single quantitative variable
- 3.2.2 Measures for several quantitative variables
- 3.2.3 Similarity measures of observations
- 3.3 Data manipulation and transformation
- 3.4 Dimension reduction: Principal component analysis
- 3.5 R and Python practice
- 3.6 Exercise
CHAPTER OBJECTIVES
3.1 Categorica data summary using tables
3.1.1 Frequency table for a single variable
Frequency table for a categorical variable
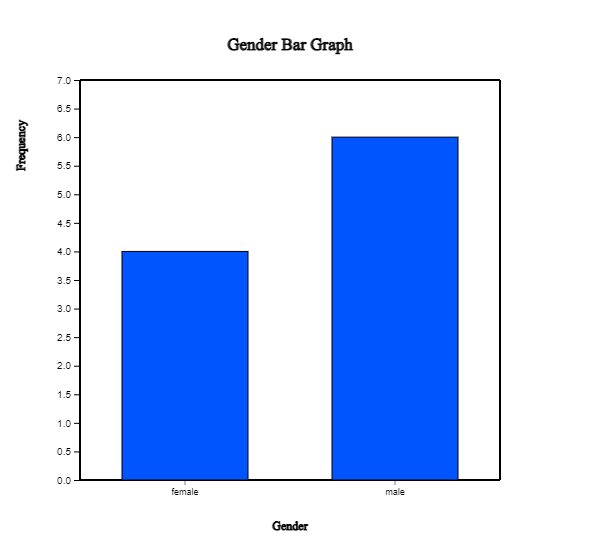
In Example 2.1.1, we drew the bar graph of the gender variable in a class using the raw data as shown in Table 3.1.1. We drew the bar graph using the frequencies of male and female students. Let's create a frequency table for this raw data of the gender variable using 『eStat』 .
| Table 3.1.1 Gender raw data |
|---|
| Gender |
| male |
| female |
| male |
| female |
| male |
| male |
| male |
| female |
| male |
| female |
[Ex] ⇨ DataScience ⇨ Gender.csv.
Answer
We discussed how to enter the gender data of Table 3.1.1 to 『eStat』 as in <Figure 2.1.1>.
If you select the gender variable as the 'Analysis Var' in the variable selection box,
a bar graph of the gender is drawn as in <Figure 3.1.1>. Then, if you click the
Frequency Table icon, ![]() ,
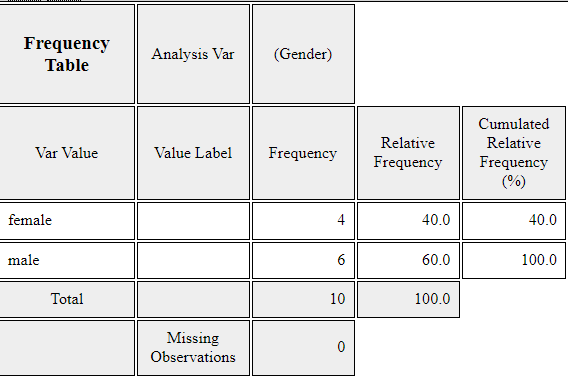
the frequency table of the gender variable will appear in the Log Area, as in <Figure 3.1.2>.
This frequency table is used to draw the bar graph or the pie chart.
,
the frequency table of the gender variable will appear in the Log Area, as in <Figure 3.1.2>.
This frequency table is used to draw the bar graph or the pie chart.
Data that examined gender (1: male, 2: female) and vegetable preference(1: lettuce, 2: spinach, 3: pumpkin, 4: eggplant) of an elementary school class can be found at the following location of 『eStat』.
[Ex] ⇨ DataScience ⇨ VegetablePrefByGender.csv.
By using 『eStat』 , find a frequency table of the vegetable preference.
Frequency table for a quantitative variable
Data of 30 otter length can be found at the following location of 『eStat』.
[Ex] ⇨ DataScience ⇨ OtterLength.csv.
Find a frequency table of the otter lengths by using the histogram module of 『eStat』.
Answer
Retrieve the data from 『eStat』 as in <Figure 3.1.3>.
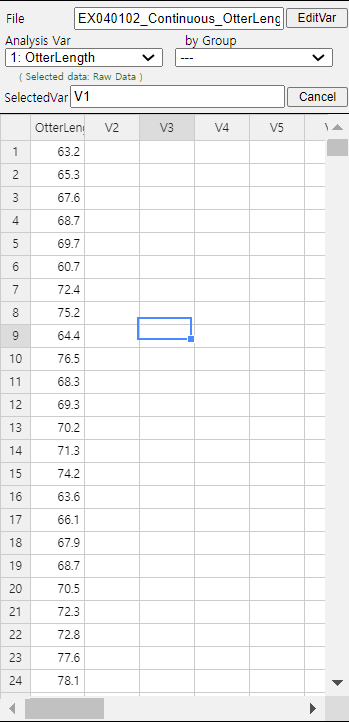
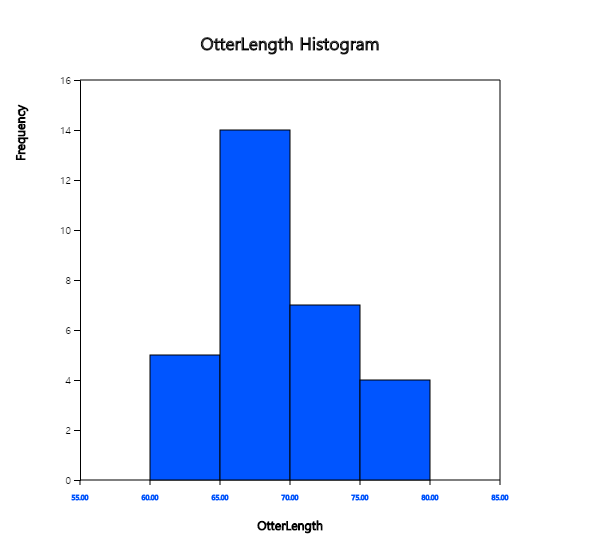
Click the Histogram Icon and then select the variable name 'OtterLength' to draw a histogram as shown in <Figure 3.1.4>.
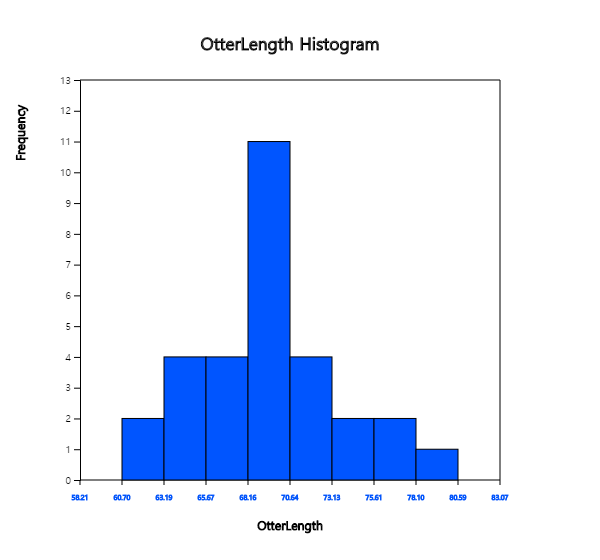
Click on the [Frequency Table] button in the options window below the histogram (<Figure 3.1.5>). Then a frequency table of the histogram intervals is shown as in <Figure 3.1.6> in the Log Area.

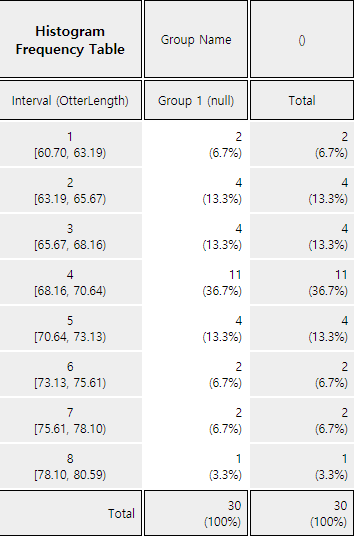
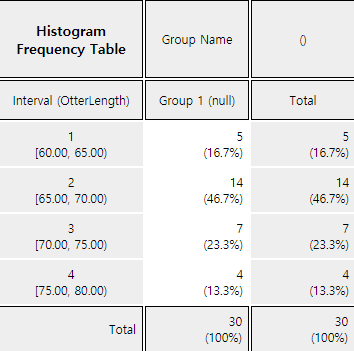
If you want to adjust the histogram intervals from 60kg with an interval length of 5kg, set ‘Interval Start’ to 60 and ‘Interval Width’ to 5 in the graph options. Press [Execute New Interval] button to display the adjusted histogram as shown in <Figure 3.1.7>. Click on [Frequency Table] button to reveal a new frequency table as in <Figure 3.1.8>.
The following data is a survey on the age of 30 people who visited a library in the morning. Draw an appropriate histogram and its frequency table using 『eStat』.
3.1.2 Two-dimensional frequecy table for two variables
Two-dimensional frequency table for two categorical variables
The two-dimensional frequency table is usually made for two qualitative variables data. In the case of two quantitative variables, We can transform the quantitative data into categorical data using interval transformation in section 3.3. Then, we can create a cross table for data on two categorical variables.
Let us discuss how to create a contingency table from the raw data of two categorical variables using the following example.
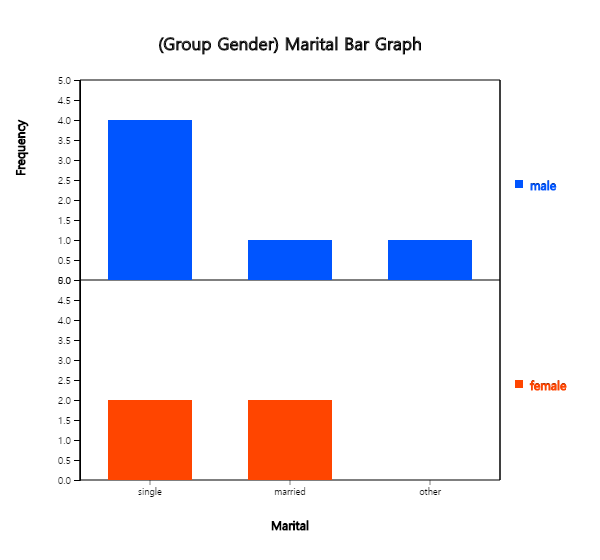
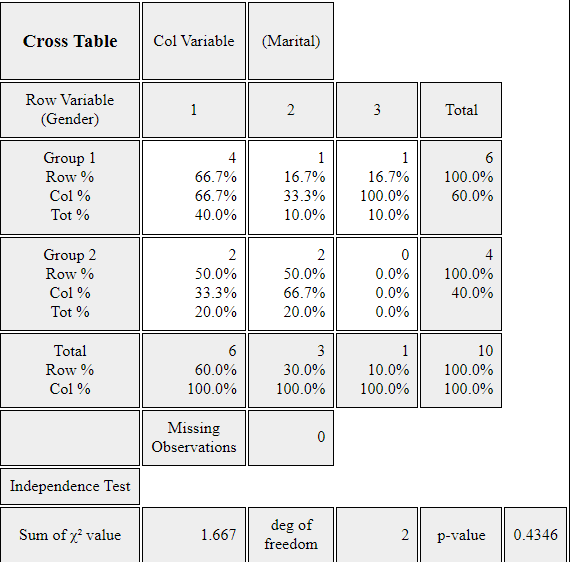
Table 3.1.2 shows survey data on Gender (1: Male, 2: Female) and Marital Status (1: Single, 2: Married, 3: Other). Note that the data used the coded values 1, 2 for Gender and 1, 2, 3 for Marital Status to save storage space. This kind of coding is common in practice. Create a two-dimensional contingency table of the marital status by Gender using 『eStat』.
| Table 3.1.2 Survey data on gender and marital status | |
|---|---|
| Gender | Marital Status |
| 1 | 1 |
| 2 | 2 |
| 1 | 1 |
| 2 | 1 |
| 1 | 2 |
| 1 | 1 |
| 1 | 1 |
| 2 | 2 |
| 1 | 3 |
| 2 | 1 |
[Ex] ⇨ DataScience ⇨ MaritalByGender.csv.
Answer
Enter the data of Gender and Marital Status in Table 3.1.2 to the sheet of 『eStat』 as in <Figure 3.1.9>. Use [Edit Var] button to enter a variable name 'Gender' and value labels 'Male' for 1 and 'Female' for 2. In the same way, enter a variable name 'Marital' and value labels 'Single' for 1, 'Married' for 2 and 'Other' for 3. The data that were edited for their value labels should be saved in JSON format file by clicking on the JSON Save icon. If you want to load this file in JSON format, you must also click on the JSON Open icon to load a file in JSON format.
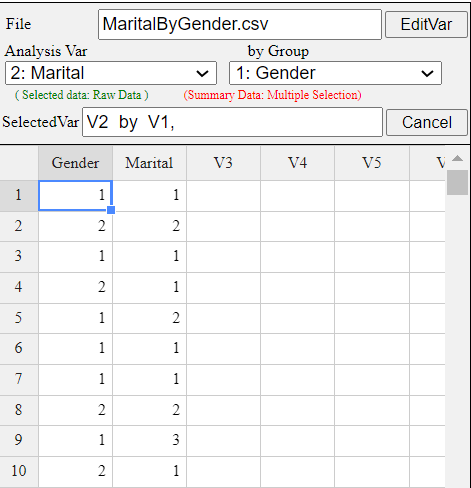
Click on the variable name 'Marital' ('Analysis Var'), and then the variable name
'Gender' ('by Group'). Then you will see a bar graph of the marital status by gender
as in <Figure 3.1.10> which is a default graph. Click the Frequency Table icon
![]() to display a two-dimensional table of the marital status by gender in the Log window
as in <Figure 3.1.11>. In this table, the ‘by Group’ variable becomes
the row variable, and the ‘Analysis Var’ becomes the column variable. This contingency table
was used to draw the bar graph of the marital status by gender, as in <Figure 3.1.10>.
to display a two-dimensional table of the marital status by gender in the Log window
as in <Figure 3.1.11>. In this table, the ‘by Group’ variable becomes
the row variable, and the ‘Analysis Var’ becomes the column variable. This contingency table
was used to draw the bar graph of the marital status by gender, as in <Figure 3.1.10>.
In an elementary school class, a survey on gender (1: male, 2: female) and favorite vegetable (1: lettuce, 2: spinach, 3: pumpkin, 4: eggplant) was conducted. The survey data can be found at the following location of 『eStat』.
Create a contingency table of the favorite vegetable by gender.
Two-dimensional frequency table for two quantitative variables
If both variables are quantitative, we need to categorize each quantitative variable by using the 'Categorize' function of the 'EditVar' button. It will be explained in section 3.3.
In a middle school, the age and gender of all teachers are surveyed. The data are saved at the following location of 『eStat』.
[Ex] ⇨ DataScience ⇨ TeacherAgeByGender.csv.
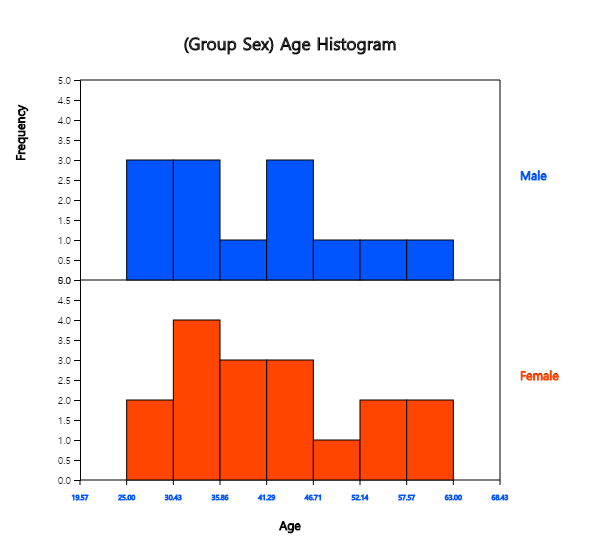
Using the histogram module of 『eStat』 , create a two-dimensional table of Age by Gender.
Answer
Retrieve the data from 『eStat』 as in <Figure 3.1.12> and enter value labels of 'Gender' as 'Male' for 1 and 'Female' for 2.
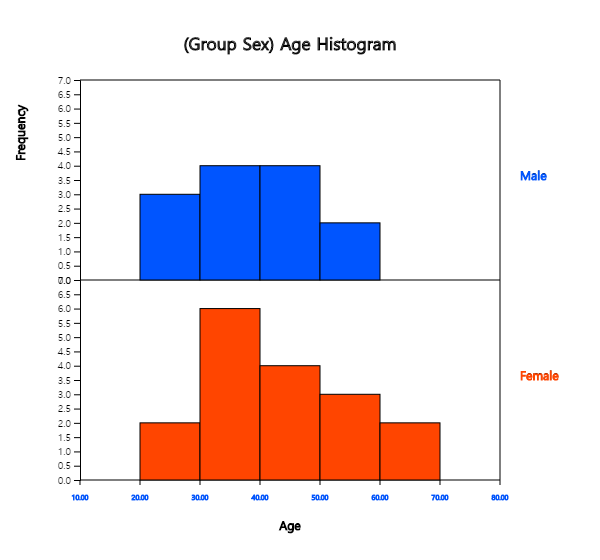
After clicking the histogram icon, select the ‘Age’ variable as 'Analysis Var', and then the ‘Gender’ variable as 'by Group'. A histogram will appear as shown in <Figure 3.1.13>.
If you click the button of 'Frequency Table' in the options window below the graph, <Figure 3.1.14>, a two-dimensional frequency table will appear in the Log window as shown in <Figure 3.1.15>.

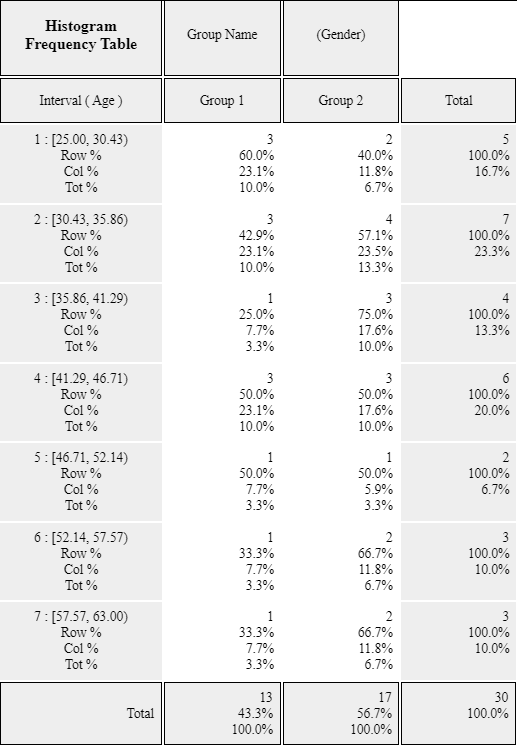
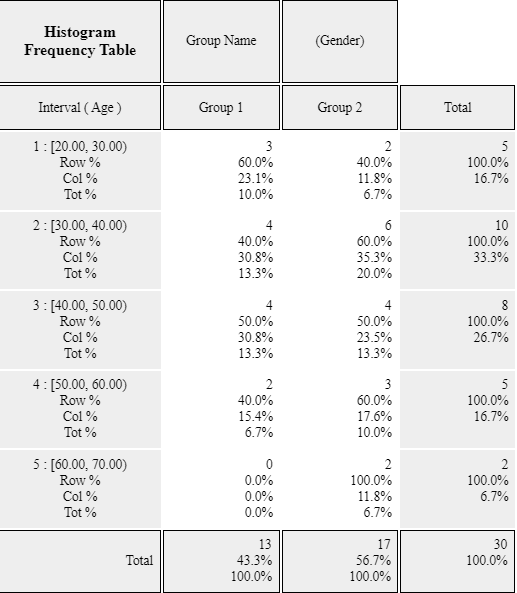
If the intervals of the histogram in <Figure 3.1.13> are to be readjusted, for example, from 20 to 10 years apart, set 'Interval Start' to 20 and ‘Interval Width’ to 10 in the graph options and press [Execute New Interval] button. Then, a histogram with the adjusted intervals appears as in <Figure 3.1.16>. We can obtain a two-dimensional frequency table with the adjusted intervals by clicking on [Frequency Table] button as shown in <Figure 3.1.17>.
According to the brushing method (1: basic method, 2: rotation method), oral cleanliness scores are examined and stored at the following location of 『eStat』.
[Ex] ⇨ DataScience ⇨ ToothCleanByBrushMethod.csv.
Create a contingency table of oral cleanliness by brushing method.
3.1.3 Multi-dimensional frequency table for several variables
Draw a \(m × m\) matrix of cross tables and a \(m\)-dimensional frequency table using the five variables in Table 2.1.3, gender, age, income, credit and purhase.
Answer
After loading the data file of Table 2.1.3, /DataScience/PurchaseByCredit20.csv,
click the bar graph matrix icon
 .
Click 'Purchase' as 'Group' variable and select 'Gender', 'Age', 'Income', 'Credit'
as 'Analysis Var'. Then the bar graph matrix, as in <Figure 3.1.17> will appear
in the graph window. If you click 'Cross Table Matrix' button below the graph,
the cross table matrix, which corresponds to the bar graph matrix will appear
in the Log table window as in <Figure 3.1.18>. If you click 'Mult-dim Frequency Table'
button, an all possible multi-dimensional frequency table using five variables, 'Purchase',
'Gender', 'Age', 'Income', and 'Credit' will appear in the Log table window
as in <Figure 3.1.19>.
.
Click 'Purchase' as 'Group' variable and select 'Gender', 'Age', 'Income', 'Credit'
as 'Analysis Var'. Then the bar graph matrix, as in <Figure 3.1.17> will appear
in the graph window. If you click 'Cross Table Matrix' button below the graph,
the cross table matrix, which corresponds to the bar graph matrix will appear
in the Log table window as in <Figure 3.1.18>. If you click 'Mult-dim Frequency Table'
button, an all possible multi-dimensional frequency table using five variables, 'Purchase',
'Gender', 'Age', 'Income', and 'Credit' will appear in the Log table window
as in <Figure 3.1.19>.
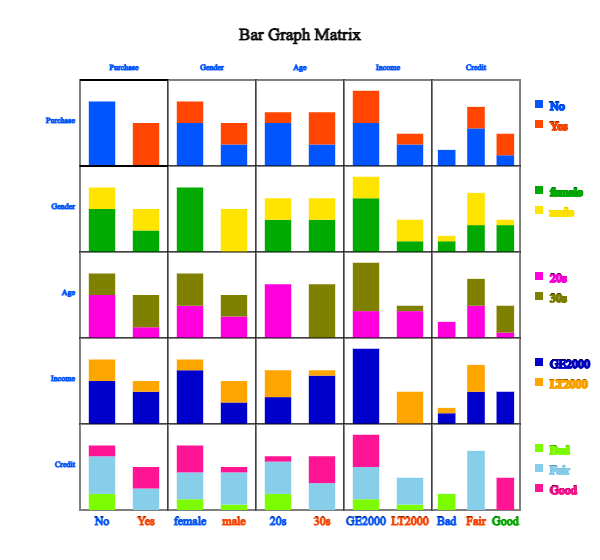
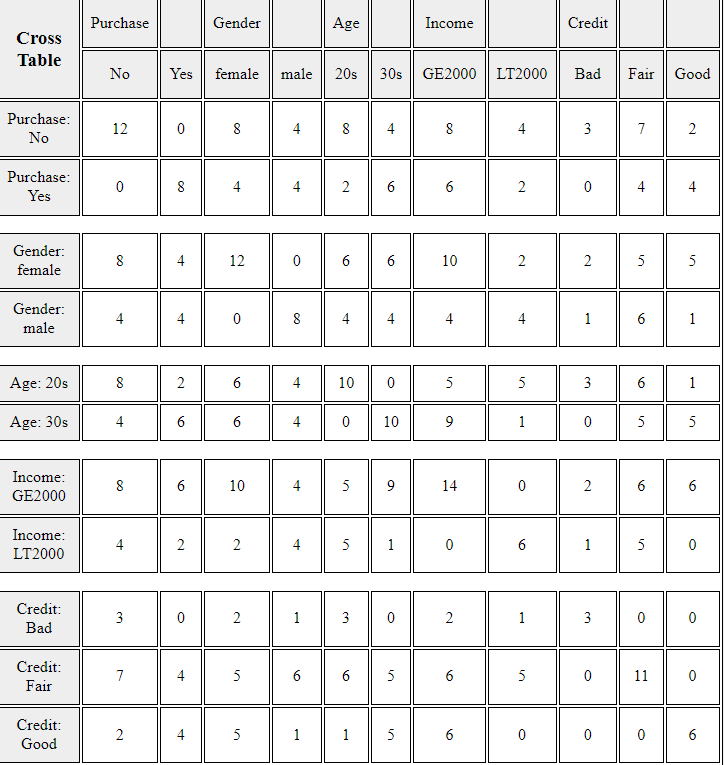
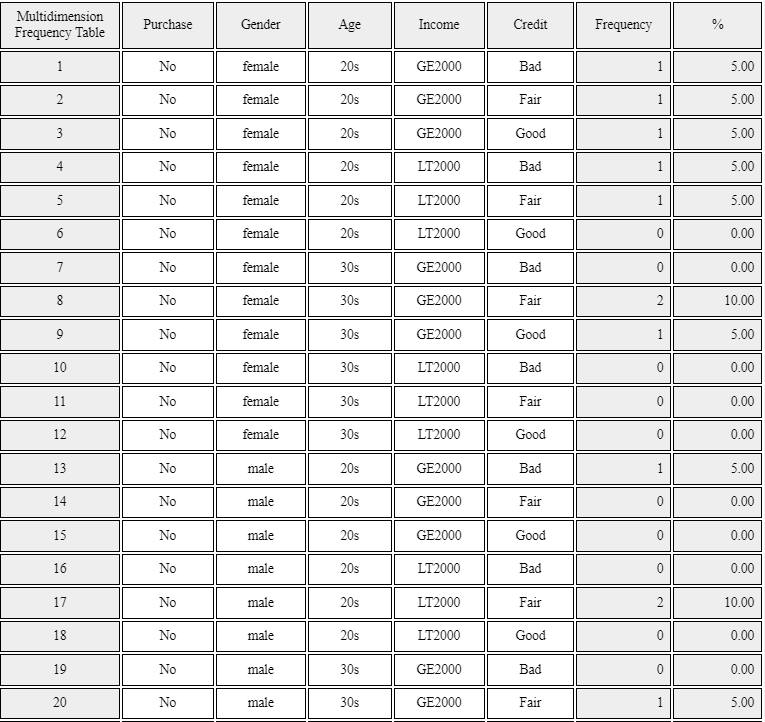
You can practice a multi-dimensional frequency table using 'Bar graph matrix' module in 『eStatU』, 'Ch 2 Bar graph Matrix' as the following example. You will see a bar graph matrix if you click the [Execute] button. Click [Cross Table Matrix] to see the graph as in <Figure 3.1.18> and click the [Multi-dimensional Frequency Table] button to see the graph as in <Figure 3.1.19>.
[Bar Graph Matrix]
3.2 Quantitative data summary using measures
3.2.1 Measures for a single quantitative variable
Measures of central tendency
A median is the value placed in the middle when data are listed in ascending order of their values, and is denoted as \(median\) if data are sampled from a population. If the number of sample data, \(n\), is an odd number, the median is the data value located at the \({\left( n+1 \above 1pt 2 \right)}^\text{th}\) when data are arranged in ascending order. If \(n\) is an even number, then the median is the average of the data values located at the \({\left( n \above 1pt 2 \right)}^\text{th}\) and \({\left( n+2 \above 1pt 2 \right)}^\text{th}\).
$$ \begin{align} median &= \left( \frac{n+1}{2}\right)^\text{th} \text{ data } & \text{if $n$ is odd}\\ &= \frac{ (\frac{n}{2})^\text{th} + \left(\frac{n+2}{2} \right)^\text{th} \text{ data }}{2} & \text{if $n$ is even} \end{align} $$ The median is not sensitive even if there is an extreme point in data, so it is often used as a measure of the central tendency when there is an extreme point.
A mode is the most frequently occurring value among data values. $$ \textit{mode} = \text{the most frequently occurred value among data values} $$ In the case of quantitative data, since there might be so many possible values, it is not reasonable to set a mode value as the most frequently occurred data value. In this case, we usually transform the quantitative data into qualitative data by dividing the data values into several not-overlapped intervals and counting the frequencies of each interval. The middle value of an interval with the highest frequency is set to the mode.
Quiz scores of seven students in a statistics class are sampled as follows.
Calculate the mean and median of this data and compare the result with 『eStat』 output.
Answer
The sample mean is calculated as follows.
\( \qquad \small \overline x ~=~ { {5 + 6 + 3 + 7 + 9 + 4 + 8} \over 7} ~=~ 6 \)
In order to find the sample median, first arrange the data in ascending order of data values as follows:
Since the sample size, 7, is an odd number, the median is \(\small {\left( 7+1 \over 2 \right)}^{th} ~=~4^{th}\) data in the arranged data as above which is 6.
To use 『eStat』, enter the data in column V1 of the sheet as in <Figure 3.2.1>. Click the Dot Graph icon and click the variable name ‘Quiz’ to see the dot graph of data as in <Figure 3.2.2>. If you check the option ‘Mean/StdDev’, you can see the location of the mean, and the interval of the standard deviation.
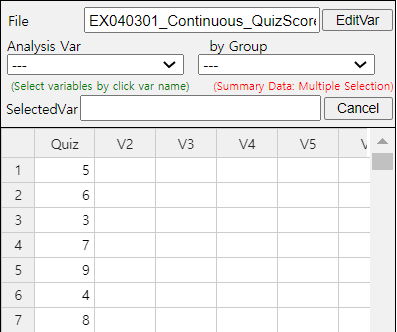
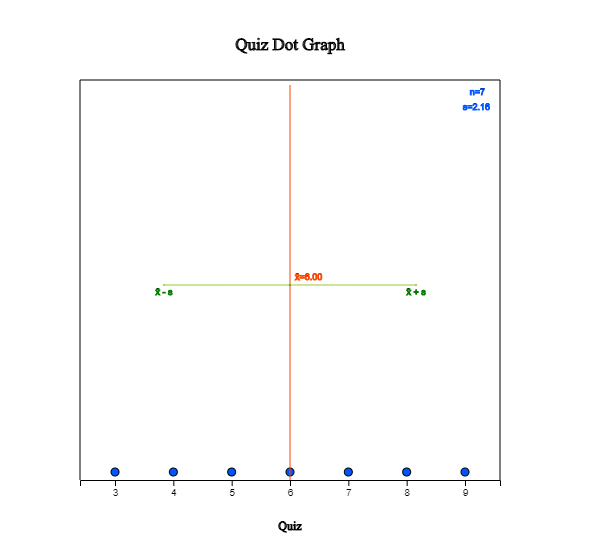
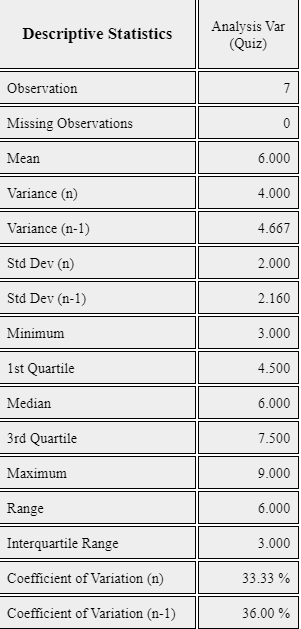
If you click the Descriptive Statistics icon, a table of all descriptive statistics will result in the Log Area as shown in <Figure 3.2.3>. It shows the mean, median, and other statistics such as the standard deviation, minimum, and maximum, etc.
You can also use 『eStatU』 to calculate the descriptive statistics and simulate the influence of extreme points. Select [Box Plot – Descriptive Statistics] from the menu of 『eStatU』 and enter data. 『eStatU』 calculates all statistics while you are entering data.
If you click the [Execute] button, two sets of dot graphs and box plots appear. The first graph is for the data you entered, and the second one is for simulation. On the second bar graph, you can click a point (circle) using your mouse and move to the other far side location of the axis (make an extreme point) to check its influence on the mean and median. You can see that the mean is changed a lot by the extreme point, but the median is not altered by the extreme point.
The lengths of 30 otters are measured (in cm), and the data are saved at the following location of 『eStat』.
If a frequency table of visitors’ age in a library is as shown in Table 3.2.1, find the mode of the age based on this frequency table.
| Table 3.2.1 Frequency table of visitor's age in a libray | |
|---|---|
| Age Interval | Frequency |
| [20.00, 30.00) | 2 ( 6.7%) |
| [30.00, 40.00) | 7 (23.3%) |
| [40.00, 50.00) | 7 (23.3%) |
| [50.00, 60.00) | 9 (30.0%) |
| [60.00, 70.00) | 3 (10.0%) |
| [70.00, 80.00) | 2 ( 6.7%) |
| Total | 30 (100%) |
Answer
The interval [50.00, 60.00) has the highest frequency, 9, and the median is the mid value of the interval [50.00, 60.00), which is 55.
Another variant is a weighted mean in which each measurement is multiplied by a constant weight to obtain the mean. The grade point average for college students, which uses the weights of credit hours, is an example of the weighted mean. The price index. which uses the weights of the total amount of sales of the goods, is another example of the weighted mean. If \( x_{1} ,x_{2}, \dots , x_{n} \) are the data values and their weights are \( w_{1} , w_{2} ,\dots , w_{n} \), then the weighted mean is defined as the following. \[ \text{Weighted Mean} ~=~ { {w_{1} x_{1} +w_{2} x_{2} + \cdots + w_{n} x_{n}} \over {w_{1} + w_{2} + \cdots + w_{n}} } ~=~ { {\sum _{i=1} ^{n} w_{i} x_{i}} \over {\sum _{i=1} ^{n} w_{i}} } \]
Eight referees in an Olympic gymnastics Game judged a player as follows:
Find the mean and median of this data. Also, find the trimmed mean, which excludes the minimum and the maximum. Compare both results.
Answer
This data is not a sample but a population of eight. The mean is as follows.
\( \qquad \small \mu ~=~ (9.0 + 9.5 + 9.3 + 7.2 + 10.0 + 9.1 + 9.4 + 9.0) / 8 ~=~ 72.5 / 8 ~=~ 9.063 \)
Since the number of data is \( \small N\) = 8 which is an even number, the median is the average of the 4th and the 5th data in the ordered list as follows:
Therefore, the median is the average of 9.1 and 9.3, which is 9.2. The trimmed mean is the average of the remaining numbers, except the minimum of 7.2 and the maximum of 10.0.
\( \qquad \small \text{Trimmed Mean} ~=~ (9.0 + 9.0 + 9.1 + 9.3 + 9.4 + 9.5) / 6 ~=~ 55.3 / 6 ~=~ 9.217\)
In this data, the median or the trimmed mean is more representative of the data than the arithmetic mean.
A student took three courses in History (two credits), Math (four credits), and English (three credits) last semester. He got an A in History, a B in math, and a C in English. Calculate the mean and the weighted mean with the number of credits if A is rated 4 points, B is 3 points, and C is 2 points.
Answer
\( \small \qquad \text{Mean = } \frac{4 + 3 + 2 }{3} = 3 \)
\( \small \qquad \text{Weighted Mean = } \frac { 2×4 + 4×3 + 3×2 } { 2 + 4 + 3 } = \frac{ 8 + 12 + 6} {9} = 2.89 \)
The weighted mean is less than the mean because although the grade in History, which has two credits, was A, the grade in English, which has three credits, was relatively poor, C.
Measures of dispersion
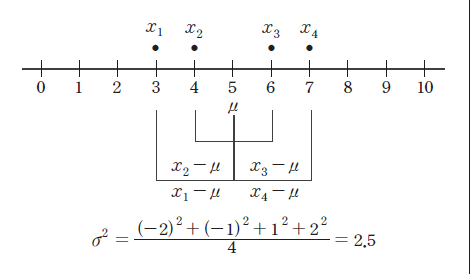
A standard deviation is defined as the square root of the variance. A population standard deviation is denoted as \(\sigma\), and a sample standard deviation is denoted as \(\s\). The variance is not easy to interpret because it is an average of the squared distances. However, since the standard deviation is the square root of the variance, it is interpreted as an average distance from each data value to the mean. $$ \begin{align} \sigma &=~ \sqrt {\sigma^2} \\ s &=~ \sqrt {s^2} \end{align} $$
In Example 3.2.1, the mean of the following sample data was 6.
Calculate a sample variance and a sample standard deviation of this data.
Answer
The sample mean was calculated as follows.
\( \small \qquad \overline x ~=~ { { 5 + 6 + 3 + 7 + 9 + 4 + 8 } \over 7 } ~=~ 6. \)
Since this data is sampled, the sample variance is calculated as follows. Note that it is divided by (7-1).
\( \small \qquad s^{2} ~=~ { {(5-6)^{2} +(6-6)^{2} +(3-6)^{2} +(7-6)^{2} +(9-6)^{2} +(4-6)^{2} +(8-6)^{2}} \over {(7-1)} } =~ { {28} \over {6} } ~=~4.667 \)
The sample standard deviation is the square root of the sample variance.
\( \small \qquad s~=~ \sqrt {s ^{2}} ~=~ \sqrt {4.667} ~=~2.16 \)
These values coincide with the output of 『eStat』 in <Figure 3.2.3> and the output of 『eStatU』.
A company's average weekly sales was 1.36 billion dollars, and its standard deviation was 0.28 billion dollars. If the same data were made in monthly sales, the average was 5.44 billion dollars, and its standard deviation was 0.5 billion dollars. Calculate a coefficient of variation for each case and compare.
Answer
The coefficient of variation in weekly sales is as follows.
\( \qquad \small \frac{0.28}{1.36} \times 100 ~=~ 20.6\%, \)
The coefficient of variation in monthly sales is as follows.
\( \qquad \small \frac{0.50}{5.44} \times 100 ~=~ 9.2\%. \)
Therefore, we can see that the variation in monthly sales is smaller than the variation in weekly sales.
A \(p\)-percentile implies roughly the percent data when data are arranged in ascending order from small to large. $$ p\text{-percentile} = p\%~ \text{of observations} \le \text{to this value and} ~(100-p)\% ~\ge~ \text{this value.} $$ Note that if the data size is small, a single observation may fall into several percentiles according to this definition. An interquartile range is a measure to complement the disadvantage of the range. The 25 percentile of the data is called the 1st quartile (Q1), the 50 percentile is called the 2nd quartile (Q2) or median, and the 75 percentile is called the 3rd quartile (Q3). The interquartile range (IQR) is the range between the 3rd quartile and the 1st quartile. $$ \text{interquartile range (IQR) = Q3 - Q1 } $$ One simple way to calculate Q1 and Q3 is to arrange the data in ascending order and divide it into two pieces with an equal number of data. If there is an odd number of data points, we add the median to the data, making the number of data points even. Q1 is the median of the first half of the data, and Q3 is the median of the second point.
Answer
The maximum of the data is 9, and the minimum is 3. Therefore, range is as follows.
\( \qquad \small \text{Range} ~=~ 9 \;–\; 3 ~=~ 6 \)
To find the quartiles of the data, first arrange the data in ascending order as follows.
The median of these numbers is the average of \( ({4 \over 2})^\text{th} \) and \( ({4 \over 2 + 1})^\text{th} \) data.
\( \qquad \small \text{Median} ~=~ \frac{(5 + 7)}{2} ~=~ 6 \)
To calculate quartiles, since the number of data is even, we divide data into two pieces as follows:
The first quartile Q1 is the median of {3, 5}, which is Q1 = 4. The third quartile Q3 is the median of {7. 9}, which is Q3 = 8. So, the interquartile range IQR is as follows.
\( \qquad \small \text{IQR = Q3} \;-\; \text{Q1 = 8} \;-\; 4 = 4 \)
Answer
The maximum of the data is 9 and the minimum is 3. Therefore, the range is as follows.
\( \qquad \small \text{Range} ~=~ 9 ~–~ 3 ~=~ 6. \)
In order to find quartiles of data, first arrange the data in ascending order as follows.
The median of the data is the data value of \( ({{7+1} \over 2})^\text{th} ~=~4^\text{th} \) which is 6.
In order to calculate the quartiles, since the number of data is odd, we insert the median into the data, and divide the data into two pieces as follows.
The first quartile Q1 is the median of {3, 4, 5, 6} which is Q1 = 4.5. The third quartile Q3 is the median of [6, 7. 8, 9] which is Q3 = 7.5. So, the interquartile range IQR is as follows.
\( \qquad \small \text{IQR = Q3 - Q1 = 7.5} \;–\; 4.5 \;=\; 3 \)
These values of Q1, Q3 and IQR coincide with the output of 『eStat』 in <Figure 3.2.3>, and the output of 『eStatU』.
Answer
Using the menu [Box Plot – Descriptive Statistics] in 『eStatU』 , if you enter the data and click the [Execute] button, the dot plot and the box plot appear as in <Figure 3.2.6>.
In a middle school, the ages of all teachers with their gender were surveyed, and the data can be found at the following location of 『eStat』.
[Ex] ⇨ DataScience ⇨ TeacherAgeByGender.csv
Answer
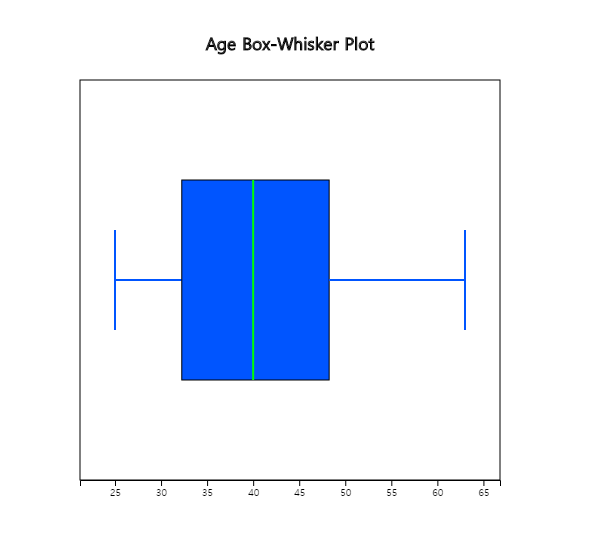
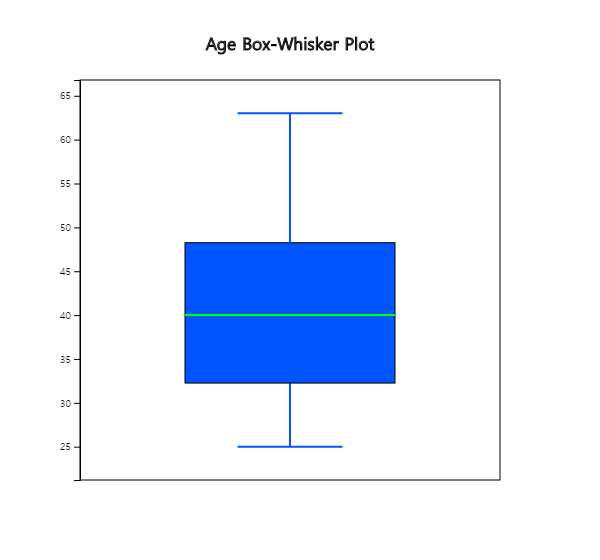
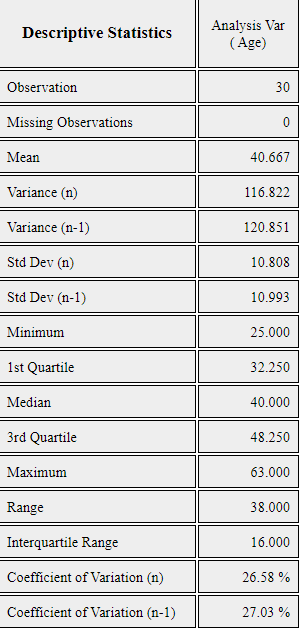
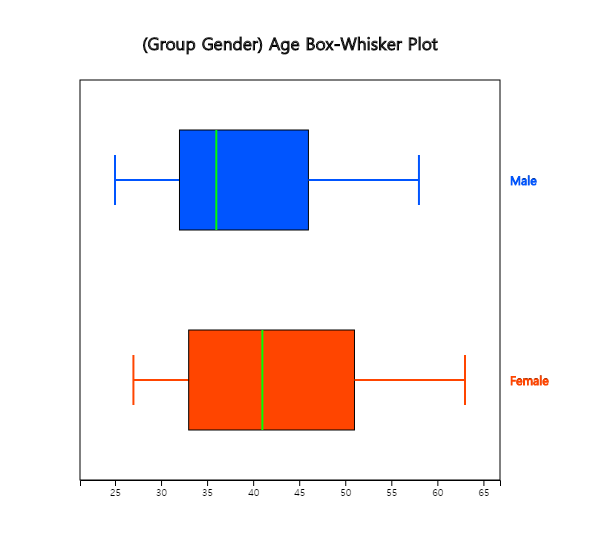
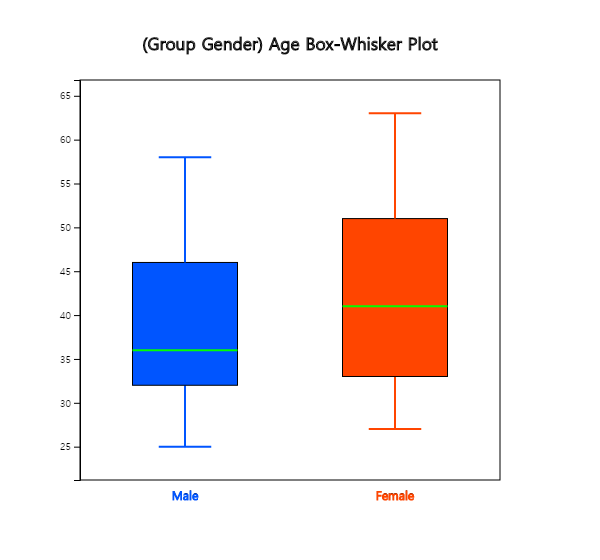
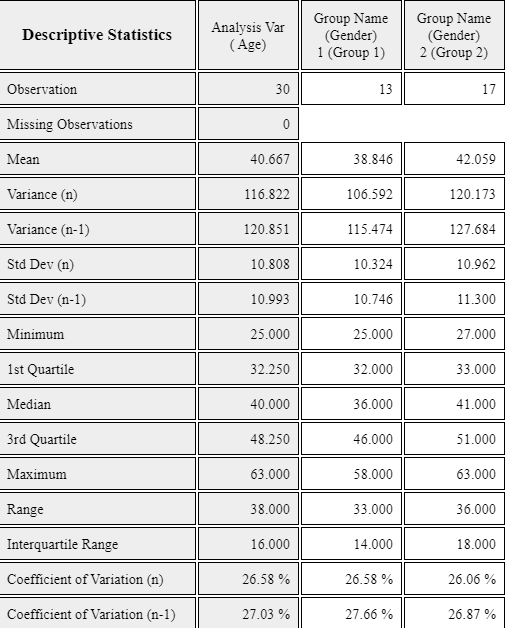
We examined the effect of Vitamin C on tooth growth in Guinea Pigs. The response is the length of odontoblasts (cells responsible for tooth growth) in 60 guinea pigs. Each animal received one of three dose levels of vitamin C (0.5, 1, and 2 mg/day) by one of two delivery methods: orange juice or ascorbic acid (a form of vitamin C coded as VC). Data can be found at the following location of 『eStat』.
[Ex] ⇨ DataScience ⇨ ToothGrowth.csv
Data format:
| V1 | length | numeric | Tooth length |
| V2 | supp | factor | Supplement type (VC or OJ). |
| V3 | dose | numeric | Dose in milligrams/day |
3.2.2 Measures for several quantitative variables
Two quantitative variables
Suppose there are two quantitative variables denoted as \(X\) and \(Y\) with means \(\mu_X\), \(\mu_Y\), and variances \(\sigma_X^2 , \sigma_Y^2 \) respectively. Suppose \(n\) number of sample data of each variable are observed and denoted as \( (x_1 , y_1 ), (x_2 , y_2 ), ... , (x_n , y_n ) \). We observe the data using a scatter plot where each data is considered as points in a two-dimensional X-Y plane, Means of the data, \( (\overline{x}, \overline{y} ) \), are the center of the data in the plane. Sample variances, \(s_x^2\) and \(s_y^2 \) are measures of dispersion in each variable.
Since data can be scattered around the X-Y plane, which implies two variables are not related or can be concentrated around a line, which implies two variables have a strong relation, a covariance measure, \(\sigma_{XY}\) in case of population, is used to measure a relation between two variables. The sample covariance, \( s_{xy}\), is defined by the following formula. $$ s_{xy} ~ =~ \frac{1}{n-1} \sum _{i=1} ^{n} (x_{i} - \overline x ) (y_{i} - \overline y ) $$ The covariance implies the total average of the values obtained by multiplying the x-axis distance and the y-axis distance from each data point to the data mean point \( (\overline{x}, \overline{y} ) \) in the X-Y plane. Therefore, if many points are on the upper right and lower left of the mean point, the covariance has a positive value, indicating a positive correlation. If many points are on the upper left and lower right of the mean point, the covariance has a negative value, indicating a negative correlation. However, since covariance can increase in value depending on the unit of data, the correlation coefficient, denoted as \(\rho_{XY}\) in case of population, is used as a measure of relation and defined as follows. $$ \rho_{XY} ~=~ \frac {\sigma_{XY}}{\sigma_X \sigma_Y } $$ The sample correlation coefficient, \( s_{xy} \) is defined as follows. $$ r_{xy} ~=~ \frac{s_{xy}}{s_x s_y} ~=~ \frac {\sum _{i=1} ^{n} (x_{i} - \overline{x} )(y_{i} - \overline{y} )} {\sqrt {\sum _{i=1} ^{n} (x_{i} - \overline{x} ) ^{2} \sum _{i=1} ^{n} (y_{i} - \overline{y} ) ^{2}}} $$ The correlation coefficient is a variation of the covariance and can only have values between -1 and +1. When the correlation coefficient is close to +1, the two variables are said to have a strong positive correlation. When the correlation coefficient is close to -1, the two variables are said to have a strong negative correlation. When the correlation coefficient is close to 0, there is no correlation between the two variables.
The characteristics of the correlation coefficient are as follows.
| Table 3.2.2 Advertising costs and sales (unit: 1 million USD) | ||
|---|---|---|
| Company | Advertise (x) | Sales (y) |
| 1 | 4 | 39 |
| 2 | 6 | 42 |
| 3 | 6 | 45 |
| 4 | 8 | 47 |
| 5 | 8 | 50 |
| 6 | 9 | 50 |
| 7 | 9 | 52 |
| 8 | 10 | 55 |
| 9 | 12 | 57 |
| 10 | 12 | 60 |
Answer
It is convenient to make the following table to calculate the sample covariance and correlation coefficient. We can also use this table for calculations in regression analysis.
| Table 3.2.3 A table for calculating the covariance | |||||
|---|---|---|---|---|---|
| Number | \(x\) | \(y\) | \(x^2\) | \(y^2\) | \(xy\) |
| 1 | 4 | 39 | 16 | 1521 | 156 |
| 2 | 6 | 42 | 36 | 1764 | 252 |
| 3 | 6 | 45 | 36 | 2025 | 270 |
| 4 | 8 | 47 | 64 | 2209 | 376 |
| 5 | 8 | 50 | 64 | 2500 | 400 |
| 6 | 9 | 50 | 81 | 2500 | 450 |
| 7 | 9 | 52 | 81 | 2704 | 468 |
| 8 | 10 | 55 | 100 | 3025 | 550 |
| 9 | 12 | 57 | 144 | 3249 | 684 |
| 10 | 12 | 60 | 144 | 3600 | 720 |
| Sum | 64 | 497 | 766 | 25097 | 4326 |
| Mean | 8.4 | 49.7 | |||
The number of data \(n\) = 10, and the terms that are necessary to calculate the covariance and correlation coefficient are as follows:
\(\small \quad SXX = \sum_{i=1}^{n} (x_i - \overline x )^{2} = \sum_{i=1}^{n} x_{i}^2 - n{\overline x}^{2} = 766 - 10×8.4^2 = 60.4 \)
\(\small \quad SYY = \sum_{i=1}^{n} (y_i - \overline y )^{2} = \sum_{i=1}^{n} y_{i}^2 - n{\overline y}^{2} = 25097 - 10×49.7^2 = 396.1 \)
\(\small \quad SXY = \sum_{i=1}^{n} (x_i - \overline x )(y_i - \overline y ) = \sum_{i=1}^{n} x_{i}y_{i} - n{\overline x}{\overline y} = 4326 - 10×8.4×49.7 = 151.2 \)
\(\small SXX, SYY, SXY \)represent the sum of squares of \(\small x_{i}\), the sum of squares of \(\small y_{i}\), the sum of squares of \(\small x_{i}, y_{i}\). Hence, the sample covariance and correlation coefficient are as follows:
\(\small \quad s_{xy} = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \overline x )(y_i - \overline y ) = \frac{151.2}{10-1} = 16.8 \)
\(\small \quad r = \frac {\sum_{i=1}^{n} (x_i - \overline x )(y_i - \overline y )} { \sqrt{\sum_{i=1}^{n} (x_i - \overline x )^{2} \sum_{i=1}^{n} (y_i - \overline y )^{2} } } = \frac{151.2} { \sqrt{ 60.4 × 396.1 } } = 0.978 \)
This value of the correlation coefficient is consistent with the scatter plot which shows a strong positive correlation of the two variables.
[]
Several quantitative variables
Suppose there are \(m\) quantitative variables denoted as \(X_1 , X_2 , ... , X_m \) with a mean vector $$ \left [ \matrix {\mu_1 \cr \mu_2 \cr ... \cr \mu_m } \right ] $$ and a \(m \times m \) variance-covariance matrix as follows. $$ \left [ \matrix {\sigma_{1}^2 & \sigma_{12} & ... & \sigma_{1m} \cr \sigma_{21} & \sigma_{2}^2 & ... & \sigma_{2m} \cr ... & ... & ... & ... \cr \sigma_{m1} & \sigma_{m2} & ... & \sigma_{m}^2 } \right ] $$ Suppose \(n\) number of sample data of each variable are observed and denoted as \(n \times m \) matrix as follows. $$ \left [ \matrix {x_{11} & x_{12} & ... & x_{1m} \cr x_{21} & x_{22} & ... & x_{2m} \cr ... & ... & ... & ... \cr x_{n1} & x_{m2} & ... & x_{mm} } \right ] $$ We usually observe the data using a scatter plot matrix. The sample mean vector is $$ \overline {\boldsymbol x} = \left [ \matrix {\overline x_1 \;\; \overline x_2 \;\; ... \;\; \overline x_m } \right ] $$ and the \(m \times m \) sample variance-covariance matrix \(S\) is as follows. $$ S = \left [ \matrix {s_{1}^2 & s_{12} & ... & s_{1m} \cr s_{21} & s_{2}^2 & ... & s_{2m} \cr ... & ... & ... & ... \cr s_{m1} & s_{m2} & ... & s_{m}^2 } \right ] $$ Note that the sample variance-covariance matrix \(S\) is symmetric. The sample correlation matrix \(R\) is denoted as follows. $$ R = \left [ \matrix {1 & r_{12} & ... & r_{1m} \cr r_{21} & 1 & ... & r_{2m} \cr ... & ... & ... & ... \cr r_{m1} & r_{m2} & ... & 1 } \right ] $$
Answer
You can easily find all statistics using the below 'Scatter Plot Matrix] module in 『eStatU』. After you enter 'Species' data to Y variable and other data to X1, X2, X3, X4 variables, click [Execute] button. Then, the scatter plot matrix will appear in the graph window. If you click [Multivariate Stat] button below the graph, then basic statistics, covariances and correlations on four quantitative variables of each group and total data will appear in the table window.
[Scatter Plot Matrix / Parallel Coordinate Plot / Multivariate Stat]
3.2.3 Similarity measures of observations
Suppose there are two observations \(\boldsymbol x = (x_1 , x_2 , ... , x_m )\) and \(\boldsymbol y = (y_1 , y_2 , ... , y_m )\) which have \(m\) variables. Since the dissimilarity measure is a kind of distance, it is usually denoted as \(d(\boldsymbol x , \boldsymbol y)\). The covariance or correlation coefficient in the previous section is a distance measure between data of variables (column). Commonly used distance measures between data of observations (rows) are summarized in Table 3.2.4 according to the data type. A simple match coefficient for the qualitative data is used to validate the accuracy of a classification model.
| Table 3.2.4 Distance measures between data of observations | ||
|---|---|---|
| Data type | Distance | Note |
| Qualitative | \( d(\boldsymbol x , \boldsymbol y) = \frac {f_{00} + f_{11}}{f_{00}+f_{01}+f_{10}+f_{11}} \) |
Simple match coefficient \(f_{00}\) : number of variables such as \(x_j = 0\) and \(y_j = 0 \) \(f_{01}\) : number of variables such as \(x_j = 0\) and \(y_j = 1 \) \(f_{10}\) : number of variables such as \(x_j = 1\) and \(y_j = 0 \) \(f_{11}\) : number of variables such as \(x_j = 1\) and \(y_j = 1 \) |
| Quantitative | \( d(\boldsymbol x , \boldsymbol y) = \left ( \sum _{j=1} ^{m} |x_{j} - y_{j} | ^{r} \right ) ^{1/r} \) | Minkowski distance |
| if \(r\) = 1, it is called \(L_1 \) distance. \( d(\boldsymbol x , \boldsymbol y) = \sum _{j=1} ^{m} |x_{j} - y_{j} | \) |
Manhattan distance or city block distance | |
| if \(r\) = 2, it is called \(L_2 \) distance. \( d(\boldsymbol x , \boldsymbol y) = \left ( \sum _{j=1} ^{m} |x_{j} - y_{j} | ^{2} \right ) ^{1/2} \) |
Euclid distance | |
| if \(r\) = ∞, it is called \(L_∞ \) distance. \( d(\boldsymbol x , \boldsymbol y) = max _{j=1} ^{m} |x_{j} - y_{j} | \) |
Maximum distance | |
If there are \(n\) number of observations \( {\boldsymbol x}_1 , {\boldsymbol x}_2 , ... , {\boldsymbol x}_n \) for each of \(m\) variables, all distances between \(n\) number of observations can be expressed as a \(n \times n \) matrix \(D\) as follows. Here, \(d_{ij} \) is the distance \(d({\boldsymbol x}_{i} , {\boldsymbol x}_{j} )\) between \(i^{th}\) observation and \(j^{th} \) observation. $$ D = \left [ \matrix {d_{11} & d_{12} & ... & d_{1n} \cr d_{21} & d_{22} & ... & d_{2n} \cr ... & ... & ... & ... \cr d_{n1} & d_{n2} & ... & d_{nn} } \right ] $$
『eStatU』 provides a module to calculate a distance matrix using the square of Euclid distance or Manhattan distance as following example.
Answer
You can easily find a distance matrix using the below 'Similarity Measure] module in 『eStatU』. After you enter data of four variables to X1, X2, X3, X4 [Similarity Measure]
3.3 Data manipulation and transformation
[Ex] > DataScience > Survey.csv.
This data comprises 40 observations (rows) and 6 variables (columns). Data of categorical variables such as Gender, Marital Status, Job, and Education level are coded using numbers, and the meaning of each coded value are as follows:
V1 Gender 1:Men, 2:Female
V2 Marital Status 1: single, 2: married, 3: other
V3 Age
V4 Job 1: Office worker, 2: Civil servant, 3: Labor worker, 4: Politician, 5: Student,
6: Entrepreneur, 7: Housewife, 8: Other
V5 Education Level 1: No Education, 2: Elementary, 3: Middle School, 4: High School, 5: University
V6 Income
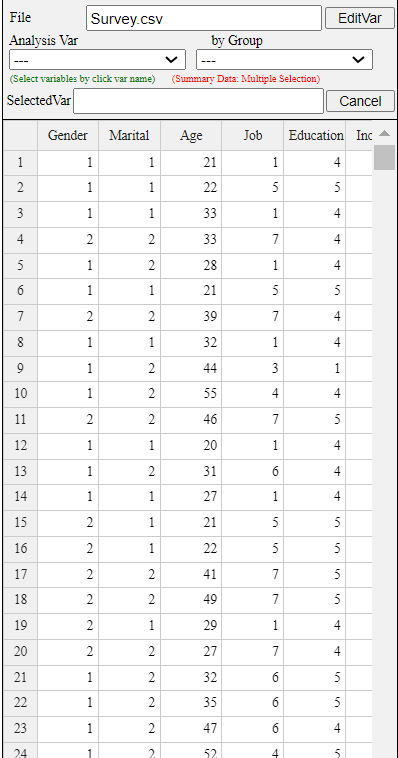
<Figure 3.3.1> Survey.csv Data
Assigning value label to the coded data
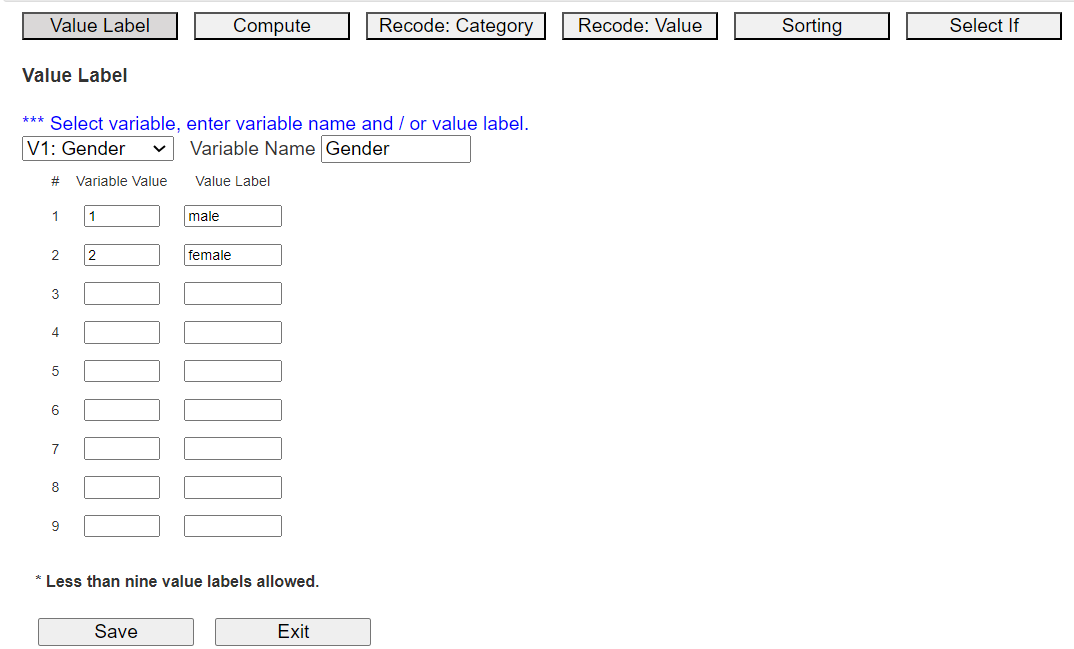
<Figure 3.3.2> [EditVar] dialog box
On the screen, 'V1: Gender' is selected, and value labels 1 and 2 are displayed. On the right side of the screen, input 'male' and 'female' as the name of the value label. Select another categorical variable, and enter the variable name and value labels similarly. We can enter value labels up to 9 categories of a variable.
After the input is finished, press the [Save] button and then the [Exit] button. The system memorizes the value labels,
but you have to save it in json format using the icon
![]() and you have to use the json load using the icon
and you have to use the json load using the icon
![]() when you open the saved file.
when you open the saved file.
Mathematical transformation
Standardization is to transform the original data into data with a mean of 0 and a variance of 1. If \(x\) is the value of a variable, \(\mu\) is the mean of the variable and \(\sigma\) is the standard deviation of the variable, a standardized variable \(z\) is to subtracts the mean from each data and divide it by the variable's standard deviation as follows. $$ \text{Standardization:} \quad z = \frac {x - \mu}{\sigma} $$
Models for data analysis often make statistical assumptions, which may not be satisfied by the data. In such cases, exponential transformation(\(exp(x)\)), log transformation(\(exp(x)\)), reciprocal transformation(\(exp(x)\)), square root transformation(\(exp(x)\)), or Box-Cox transformation of data is frequently used. $$ \text{Box-Cox transformation:} \quad \Big[ \; \matrix { \frac {x^p - 1}{p} , \,\, \text{if} \,\, p \ne\ 0 \cr log(x), \,\, \text{if} \,\, p = 0 } $$
The mathematical transformation mentioned above can be done by using Compute module in 『eStat』.
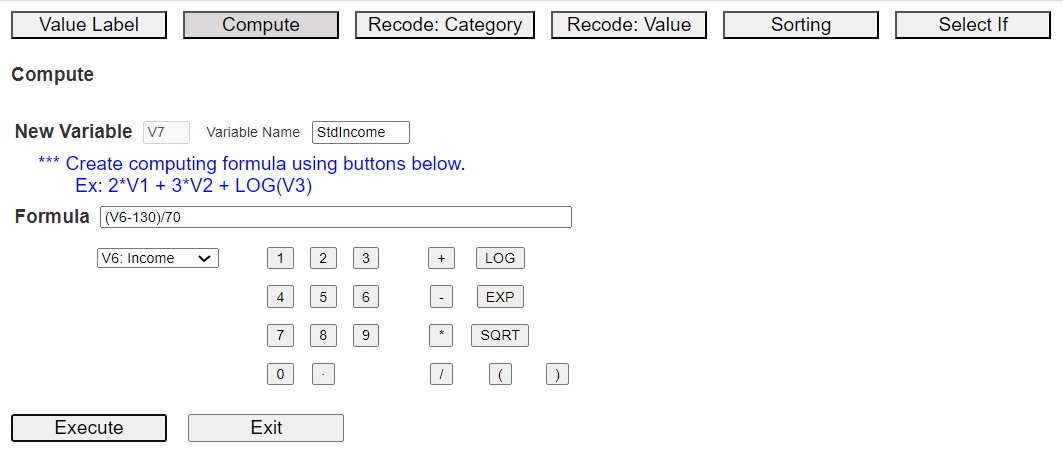
<Figure 3.3.3> Compute dialog box
Suppose the population mean of Income is 130, and its standard deviation is 70. The Standardized Income, called StdIncome, can be calculated by creating a formula (V6-130)/70 using the buttons on variables, numbers, arithmetic operators (+, -, *, /), and parenthesis. You can use buttons of LOG, EXP, SQRT functions on the Compute dialog box to make a new variable for other mathematical transformations. Give a new name to the newly created variable, such as 'StdIncome', and then click [Execute] button. The newly created data is automatically placed on the far right of the sheet, as <Figure 3.3.4>. In this example, there are currently 6 variables, so a new computed variable is created in V7, as shown in <Figure 3.3.4>.
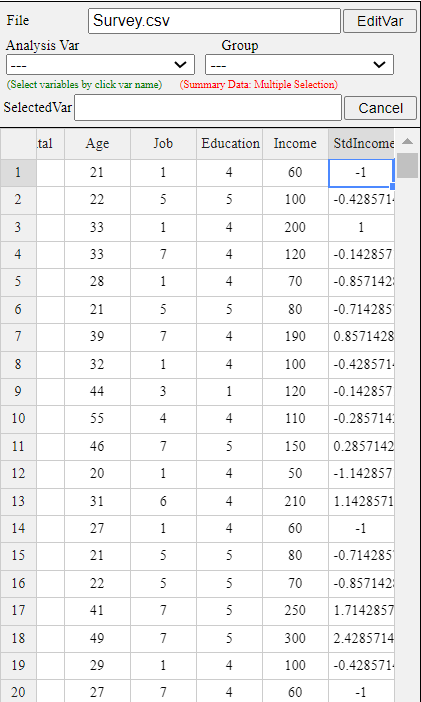
<Figure 3.3.4> Newly computed standardized data of Income
Categorization
Categorization of continuous data can be easily done using [Recode: Category] module in [EditVar] of 『eStat』 as follows.
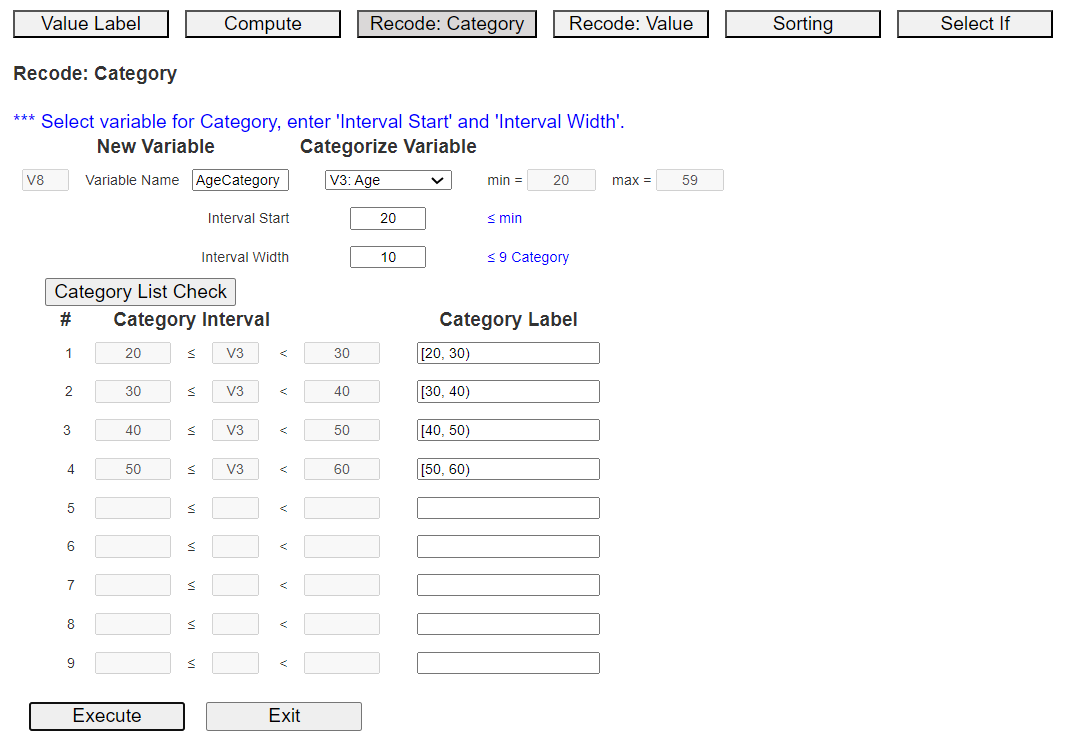
<Figure 3.3.5> Dialogue box of 'Recode: Category' module
The newly created data of the categorized variable, AgeCategory, is automatically placed on the far right of the sheet. In this example, there were 7 variables, so new categorized variable is located at V8 as shown in <Figure 3.3.6>.
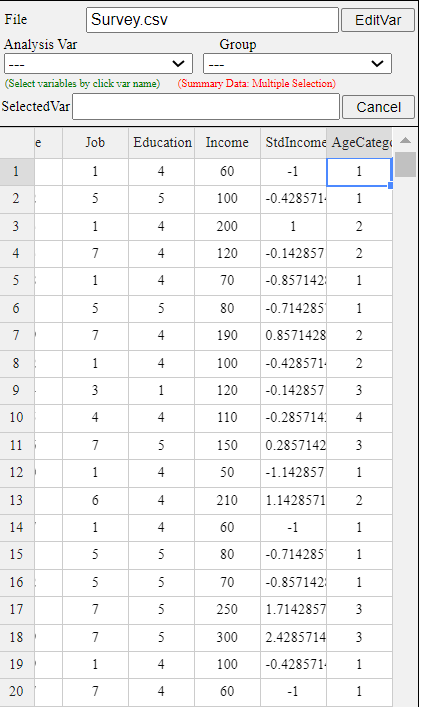
<Figure 3.3.6> New created data of 'AgeCategory'
Recoding a value of the variable
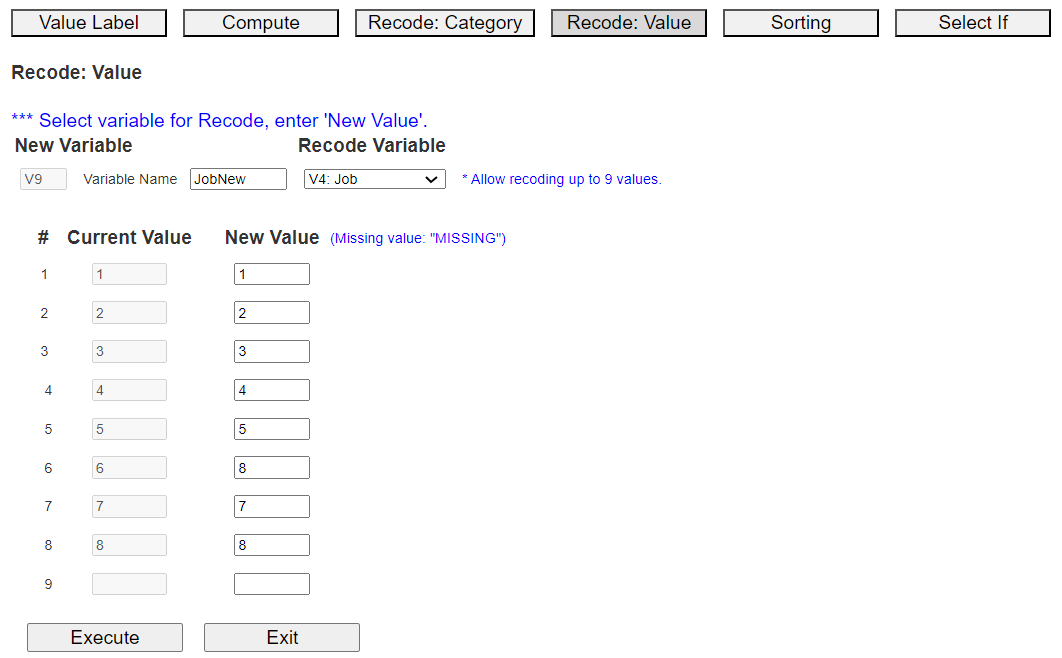
<Figure 3.3.7> Recode: Value dialog box
If you click the [Execute] button, the newly recoded variable is automatically placed on the far right of the sheet. There are currently 8 variables in this example, so a new variable is created in V9, as shown in <Figure 3.3.8>.
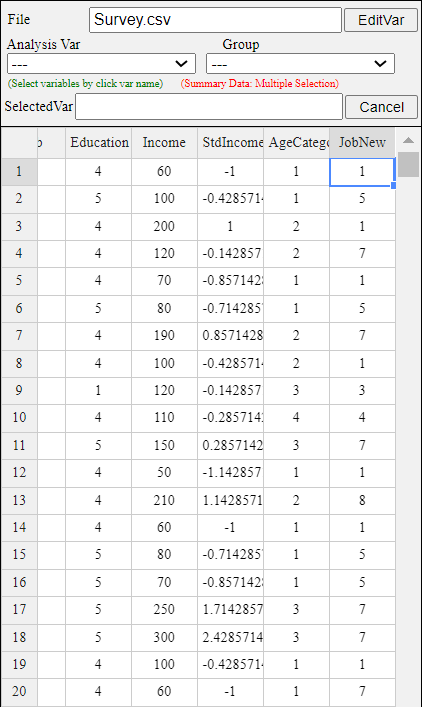
<Figure 3.3.8> Recoded value data
Sorting
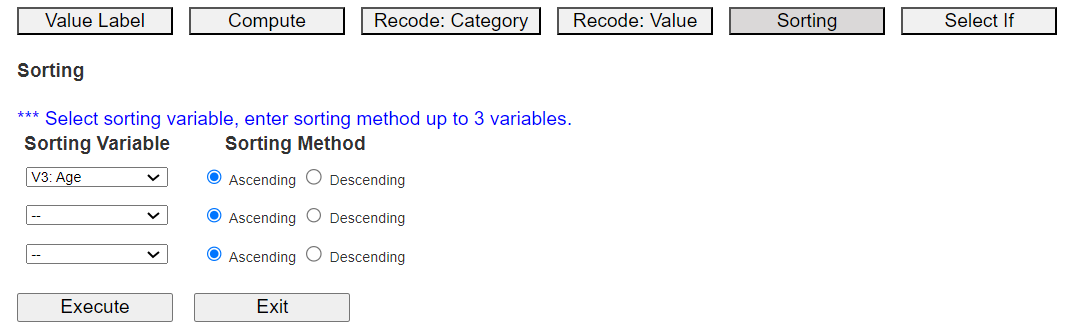
<Figure 3.3.9> Sorting dialog box
Select the first 'Sorting Variable' as Age, and 'Sorting Method' as 'Ascending', and click the [Execute] button to display the sorted data on the sheet. You can select up to three sorting key variables. After the first variable sorts the data, the second variable is sorted, and again, the first and second variables are sorted, and the third variable is sorted within sorted.
Data sorted in ascending order of Age is shown in <Figure 3.3.10>.
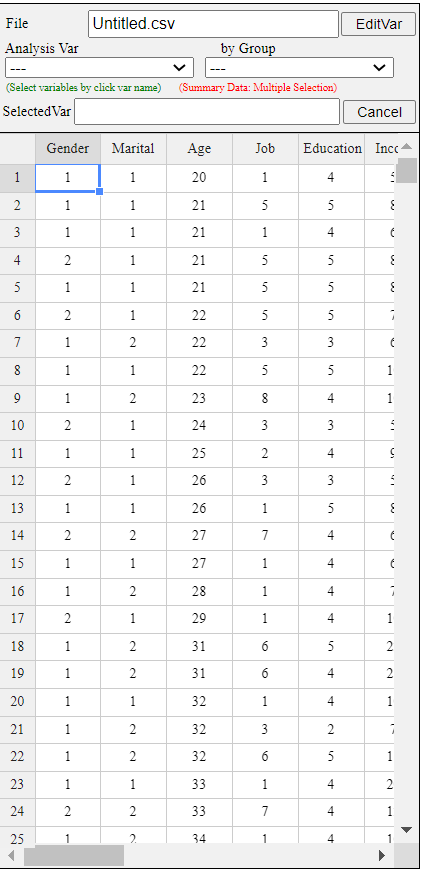
<Figure 3.3.10> Data sorted in ascending order of age
Conditional selection of data: Select If
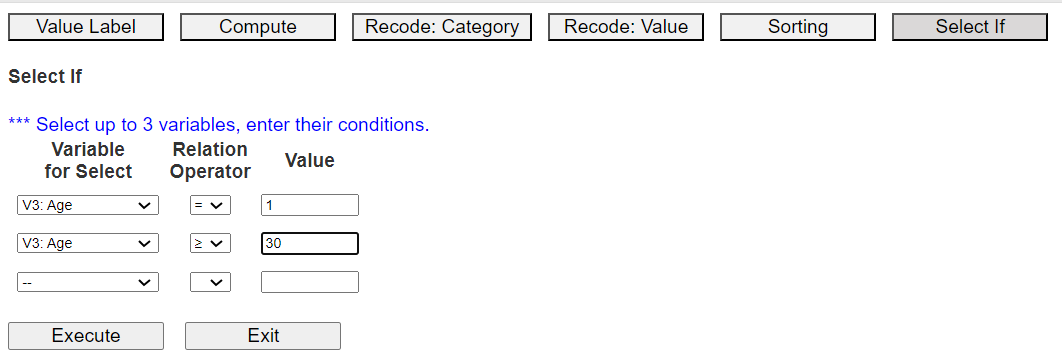
<Figure 3.3.11> 'Select If' dialog box
Select a variable, select a relational operator (=, <, ≤, >, ≥, ≠), and enter a value to complete the conditional expression. You can create conditional expressions for up to three variables. Here, select male in 'V1: Gender' and '30 years or older in V3: Age'. After creating the conditional expression, click the [Execute] button.
The data selected for males, and over 30 years of age are shown in <Figure 3.3.12>.
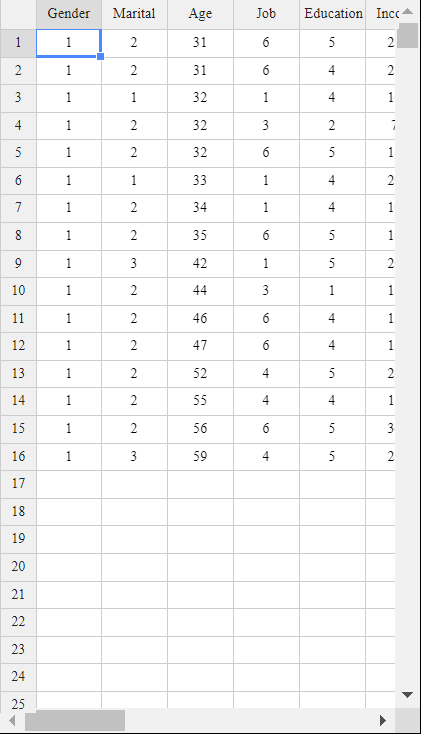
<Figure 3.3.12> Data selected for male and over 30 years of age
3.4 Dimension reduction: Principal component analysis
Reducing data size using sampling
Simple random sampling extracts a sample so that all data in the whole data set have the same probability of being selected as a sample. Both with replacement sampling and without replacement sampling can be applied, but in reality, almost all sampling is done without replacement. We can use a random number table to ensure that each data in the population has the same probability of being selected as a sample. A random number table is a table in which numbers from 0 to 9 are scattered without regularity or bias, and most programming languages provide it as a function. Stratified sampling is a method of dividing the entire data set into an appropriate number of homogeneous strata and extracting a fixed-size sample from each strata. For example, suppose you are interested in the average wage in a population of men and women. In that case, you can divide the population into two strata, men and women, and extract a sample from each strata using simple random sampling to estimate the overall average wage. In this stratified sampling method, making the data in each stratum as homogeneous as possible is good. In this case, the variance of the estimated value is smaller than in simple random sampling.
Reducing variable size using principle component analysis
Assume that a random vector \(\boldsymbol X = (X_1 , X_2 , ... , X_m )\) has a mean vector \(\boldsymbol \mu\) and a covariance matrix \(\boldsymbol \Sigma\). The diagonal elements of \(\boldsymbol \Sigma\) are the variances \(\sigma_1^2 , \sigma_2^2 , ... , \sigma_m^2 \) of each random variable. Let the eigenvalues of the covariance matrix \(\boldsymbol \Sigma\) be \(\lambda_1 , \lambda_2 , ... , \lambda_m \), which are arranged in descending order of magnitude, and let the eigenvectors corresponding to each eigenvalue be \(\boldsymbol e_1 ,\boldsymbol e_2 , ... , \boldsymbol e_m \). If \(\boldsymbol E\) is a \(m \times m\) matrix with these eigenvectors as columns such as \( \boldsymbol E = [ \boldsymbol e_1 , \boldsymbol e_2 , ... , \boldsymbol e_m ]\), the linear transformation \(\boldsymbol {Y = EX } \) creates new variables \(\boldsymbol Y = (Y_1 , Y_2 , ... , Y_m )\), which are called principal components. The principal component \(Y_j \) is a linear combination of \( X_1 , X_2 , ... , X_m \) with coefficients of the eigenvectors.
The covariance matrix \(\boldsymbol \Sigma _Y\) of the principal components \(\boldsymbol Y = (Y_1 , Y_2 , ... , Y_m )\) can be shown as follows by the properties of the eigenvalues and eigenvectors. $$ \boldsymbol {\Sigma _Y = E' \Sigma E } = \left [ \matrix {\lambda_{1} & 0 & ... & 0 \cr 0 & \lambda_{2} & ... & 0 \cr ... & ... & ... & ... \cr 0 & 0 & ... & \lambda_{m} } \right ] $$ \(\boldsymbol \Sigma _Y\) is a diagonal matrix whose diagonal elements are eigenvalues \(\lambda_1 , \lambda_2 , ... , \lambda_m \) of \(\boldsymbol \Sigma \). This means that the principal components are independent and they are orthogonal to each other geometrically. It also shows that the variance of the principal component \(Y_j\) is \(\lambda_j\). Since the eigenvalues are assumed to be \(\lambda_1 \ge \lambda_2 \ge ... \ge \lambda_m \), the first principal component \(Y_1\) has the largest variance among the linear combinations of variables \(X_1 , X_2 , ... , X_m \), and the last principal component \(Y_m\) has the smallest variance. It can be also shown that the sum of the diagonal elements of the covariance matrix \(\boldsymbol \Sigma \) (i.e., the sum of the variances of \(X_i \)'s ) is equal to the sum of all eigenvalues (i.e., the sum of the variances of the principal components \(Y_i\)'s) as follows. $$ \sigma_1^2 + \sigma_2^2 + ... + \sigma_m^2 = \lambda_1 + \lambda_2 + ... + \lambda_m $$ Since the eigenvalues are sorted in descending order of value, the variances of a few principal components can explain a large portion of the sum of the variances of \(X_1 , X_2 , ... , X_m\) variables. In other words, the variances of a small \(k\) number of principal components, \(Y_1 , Y_2 , ... , Y_k\) can explain the variances of the entire variables, \( \sigma_1^2 + \sigma_2^2 + ... + \sigma_m^2 \).
The principal component analysis often uses a correlation matrix rather than a covariance matrix because if all variables \(X_1 , X_2 , ... , X_m\) are standardized, the covariance matrix becomes the correlation matrix and the sum of the variances of the principal components \(Y_1 , Y_2 , ... , Y_m \) becomes \(m\). In this case, if the variance (eigenvalue) of a principal component is greater than 1, the contribution of this principal component is greater than the average 1. The principal component analysis uses usually \(k\) principal components, \(Y_1 , Y_2 , ... , Y_k \) whose contribution is greater than the average, instead of using all variables. Therefore, the analysis is performed by reducing the dimension to a small number of principal components. Let us practice the principal component analysis using a module in 『eStat』.
Consider the iris data, which has four variables, Sepal.Length, Sepal.Width, Petal.Length, Petal.Width. Let us find principal components and how many of them can explain total variances. If you click [Execute] button, a scatter plot matrix of the four variables will appear on the graph window with a statistics table of principal components below the graph.
The eigenvalue of the first principal component, \(\small Y_1 = -0.521 X_1 + 0.269 X_2 - 0.580 X_3 - 0.565 X_4\), is 2.918 which explains 72.96% of the total variance. The eigenvalue of the second principal component, \(\small Y_2 = 0.377 X_1 + 0.923 X_2 + 0.024 X_3 -0.067 X_4\), is 0.914 which explains 22.85% of total variance. Therefore, the variances of two principal components explain 95.81% of the total variance and only these two principal components can be used for further analysis. If you click [Principal Component Table] button, you can see the data of principal components. In this case, you can use the first two components for further analysis.
3.5 R and Python practice
R practice
[Colab]
You need to change first the working directory of R to use this data as follows.
File > Change Directory > C: > Rwork
| # read the data file |
| card <- read.csv("http://estat.me/estat/Example/DataScience/PurchaseByCredit40.csv", header=T, as.is=FALSE) |
card
ï..id Gender Age Income Credit Purchase 1 1 male 20s LT2000 Fair Yes 2 2 female 30s GE2000 Good No 3 3 female 20s GE2000 Fair No 4 4 female 20s GE2000 Fair Yes 5 5 female 20s LT2000 Bad No 6 6 female 30s GE2000 Fair No 7 7 female 30s GE2000 Good Yes 8 8 male 20s LT2000 Fair No 9 9 female 20s GE2000 Good No 10 10 male 30s GE2000 Fair Yes 11 11 female 30s GE2000 Good Yes 12 12 female 20s LT2000 Fair No 13 13 male 30s GE2000 Fair No 14 14 male 30s LT2000 Fair Yes 15 15 female 30s GE2000 Good Yes 16 16 female 30s GE2000 Fair No 17 17 female 20s GE2000 Bad No 18 18 male 20s GE2000 Bad No 19 19 male 30s GE2000 Good Yes 20 20 male 20s LT2000 Fair No 21 21 male 20s LT2000 Fair Yes 22 22 female 30s GE2000 Good No 23 23 female 20s GE2000 Fair No 24 24 female 20s GE2000 Fair Yes 25 25 female 20s LT2000 Bad No 26 26 female 30s GE2000 Fair No 27 27 female 30s GE2000 Good Yes 28 28 male 20s LT2000 Fair No 29 29 female 20s GE2000 Good No 30 30 male 30s GE2000 Fair Yes 31 31 female 30s GE2000 Good Yes 32 32 female 20s LT2000 Fair No 33 33 male 30s GE2000 Fair No 34 34 male 30s LT2000 Fair Yes 35 35 female 30s GE2000 Good Yes 36 36 female 30s GE2000 Fair No 37 37 female 20s GE2000 Bad No 38 38 male 20s GE2000 Bad No 39 39 male 30s GE2000 Good Yes 40 40 male 20s LT2000 Fair No |
| attach(card) |
| # 1 dim frequency table |
| table(Gender) |
Gender
female male
24 16
|
| # 2-dim frequency table |
| table(Gender,Purchase) |
Purchase
Gender No Yes
female 16 8
male 8 8
|
| # 3-dim frequency table |
| table(Gender,Age,Purchase) |
, , Purchase = No
Age
Gender 20s 30s
female 10 6
male 6 2
, , Purchase = Yes
Age
Gender 20s 30s
female 2 6
male 2 6
|
| # Continuous Data Basic Statistics # Read iris data |
| iris <- read.csv("http://estat.me/estat/Example/DataScience/Iris150.csv", header=T, as.is=FALSE) |
| attach(iris) |
| # mean |
| mean(Sepal.Length) |
[1] 5.843333 |
| # median |
| median(Sepal.Length) |
[1] 5.8 |
| # variance |
| var(Sepal.Length) |
[1] 0.6856935 |
| # standard deviation |
| sd(Sepal.Length) |
[1] 0.8280661 |
| # range: min, max |
| range(Sepal.Length) |
[1] 4.3 7.9 |
| # summary of basic statistics |
| summary(iris) |
ï..id Sepal.Length Sepal.Width Petal.Length
Min. : 1.00 Min. :4.300 Min. :2.000 Min. :1.000
1st Qu.: 38.25 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600
Median : 75.50 Median :5.800 Median :3.000 Median :4.350
Mean : 75.50 Mean :5.843 Mean :3.057 Mean :3.758
3rd Qu.:112.75 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100
Max. :150.00 Max. :7.900 Max. :4.400 Max. :6.900
Petal.Width Species
Min. :0.100 setosa :50
1st Qu.:0.300 versicolor:50
Median :1.300 virginica :50
Mean :1.199
3rd Qu.:1.800
Max. :2.500
|
Python practice
[Colab]
|
# Import required libraries import pandas as pd import matplotlib.pyplot as plt # Read the data file url = 'https://raw.githubusercontent.com/ogut77/DataScience/refs/heads/main/PurchaseByCredit40.csv' card = pd.read_csv(url) # Display the data print(card)
id Gender Age Income Credit Purchase
0 1 male 20s LT2000 Fair Yes
1 2 female 30s GE2000 Good No
2 3 female 20s GE2000 Fair No
3 4 female 20s GE2000 Fair Yes
4 5 female 20s LT2000 Bad No
5 6 female 30s GE2000 Fair No
6 7 female 30s GE2000 Good Yes
7 8 male 20s LT2000 Fair No
8 9 female 20s GE2000 Good No
9 10 male 30s GE2000 Fair Yes
10 11 female 30s GE2000 Good Yes
11 12 female 20s LT2000 Fair No
12 13 male 30s GE2000 Fair No
13 14 male 30s LT2000 Fair Yes
14 15 female 30s GE2000 Good Yes
15 16 female 30s GE2000 Fair No
16 17 female 20s GE2000 Bad No
17 18 male 20s GE2000 Bad No
18 19 male 30s GE2000 Good Yes
19 20 male 20s LT2000 Fair No
20 21 male 20s LT2000 Fair Yes
21 22 female 30s GE2000 Good No
22 23 female 20s GE2000 Fair No
23 24 female 20s GE2000 Fair Yes
24 25 female 20s LT2000 Bad No
25 26 female 30s GE2000 Fair No
26 27 female 30s GE2000 Good Yes
27 28 male 20s LT2000 Fair No
28 29 female 20s GE2000 Good No
29 30 male 30s GE2000 Fair Yes
30 31 female 30s GE2000 Good Yes
31 32 female 20s LT2000 Fair No
32 33 male 30s GE2000 Fair No
33 34 male 30s LT2000 Fair Yes
34 35 female 30s GE2000 Good Yes
35 36 female 30s GE2000 Fair No
36 37 female 20s GE2000 Bad No
37 38 male 20s GE2000 Bad No
38 39 male 30s GE2000 Good Yes
39 40 male 20s LT2000 Fair No
# 1 dim frequency table card['Gender'].value_counts() count Gender female 24 male 16dtype: int64 # 2 dim frequency table pd.crosstab(card['Gender'], card['Purchase']) Purchase No Yes Gender female 16 8 male 8 8# prompt: # 3 dim frequency table # table(Gender,Age,Purchase) pd.crosstab([card['Gender'], card['Age']], card['Purchase']) Purchase No Yes Gender Age female 20s 10 2 30s 6 6 male 20s 6 2 30s 2 6import pandas as pd # Load Iris dataset from UCI Machine Learning Repository url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data" columns = ['Sepal.Length', 'Sepal.Width', 'Petal.Length', 'Petal.Width', 'Species'] iris= pd.read_csv(url, header=None, names=columns) #Display the data iris Sepal.Length Sepal.Width Petal.Length Petal.Width Species 0 5.1 3.5 1.4 0.2 Iris-setosa 1 4.9 3.0 1.4 0.2 Iris-setosa 2 4.7 3.2 1.3 0.2 Iris-setosa 3 4.6 3.1 1.5 0.2 Iris-setosa 4 5.0 3.6 1.4 0.2 Iris-setosa ... ... ... ... ... ... 145 6.7 3.0 5.2 2.3 Iris-virginica 146 6.3 2.5 5.0 1.9 Iris-virginica 147 6.5 3.0 5.2 2.0 Iris-virginica 148 6.2 3.4 5.4 2.3 Iris-virginica 149 5.9 3.0 5.1 1.8 Iris-virginica 150 rows × 5 columns# mean of 'Sepal.Length' iris['Sepal.Length'].mean() np.float64(5.843333333333334) # median of 'Sepal.Length' iris['Sepal.Length'].median() 5.8 # variance of 'Sepal.Length' iris['Sepal.Length'].var() 0.6856935123042505 # standard deviation of 'Sepal.Length' iris['Sepal.Length'].std() 0.8280661279778629 # range of 'Sepal.Length' print(iris['Sepal.Length'].min(), iris['Sepal.Length'].max()) 4.3 7.9 # Summary of basic statistics iris.describe() Sepal.Length Sepal.Width Petal.Length Petal.Width count 150.000000 150.000000 150.000000 150.000000 mean 5.843333 3.054000 3.758667 1.198667 std 0.828066 0.433594 1.764420 0.763161 min 4.300000 2.000000 1.000000 0.100000 25% 5.100000 2.800000 1.600000 0.300000 50% 5.800000 3.000000 4.350000 1.300000 75% 6.400000 3.300000 5.100000 1.800000 max 7.900000 4.400000 6.900000 2.500000 |
3.6 Exercise
3.1 The following sample survey showed on the living standard and education level of 25 adults. In the living standard, 1 implies ‘high income’, 2 implies ‘average’, and 3 implies ‘low income’, and in the education level, 1 implies middle school or lower, 2 implies high school, and 3 implies college or higher.
| id | Living standard | Education level |
|---|---|---|
| 1 | 3 | 3 |
| 2 | 1 | 1 |
| 3 | 2 | 2 |
| 4 | 3 | 3 |
| 5 | 1 | 3 |
| 6 | 3 | 3 |
| 7 | 1 | 3 |
| 8 | 2 | 3 |
| 9 | 2 | 2 |
| 10 | 3 | 3 |
| 11 | 2 | 2 |
| 12 | 1 | 1 |
| 13 | 3 | 3 |
| 14 | 2 | 2 |
| 15 | 2 | 3 |
| 16 | 2 | 3 |
| 17 | 3 | 3 |
| 18 | 3 | 3 |
| 19 | 1 | 1 |
| 20 | 2 | 2 |
| 21 | 1 | 1 |
| 22 | 1 | 2 |
| 23 | 2 | 3 |
| 24 | 3 | 1 |
| 25 | 1 | 2 |
3.2 The following data shows the highest temperature (degree in Celcius) in a city on a single day in August. Find all summary measures of this data using eStat and R.
| 29, 29, 34, 35, 35, 31, 32, 34, 38, 34, 33, 31, 31, 30, 34, 35, |
| 34, 32, 32, 29, 28, 30, 29, 31, 29, 28, 30, 29, 29, 27, 28 |
3.3 Below are the entrance exam results for selecting new employees at a particular company. Find all summary measures of this data by gender using eStat and R.
| Male | Female |
|---|---|
| 49 86 40 45 48 93 97 58 58 98 58 82 52 56 50 85 80 60 62 80 62 72 65 60 64 70 78 67 69 88 |
60 72 66 65 75 78 62 64 74 58 68 72 67 61 62 72 79 71 74 73 |
3.4 The age and purchasing status (Y: purchase, N: non-purchase) of 10 people visiting a particular store were investigated as follows.
| Age | Purchasing |
|---|---|
| 23 | Y |
| 29 | N |
| 34 | Y |
| 44 | Y |
| 58 | N |
| 50 | Y |
| 46 | Y |
| 21 | Y |
| 22 | N |
| 30 | N |
3.5 The results of observing the typing speed (X) and number of errors (Y) that 10 typists input a certain amount of documents into a computer are as follows.
| Gender | X (typing speed, unit: seconds) | Y (number of errors) |
|---|---|---|
| M | 65 | 6 |
| M | 60 | 9 |
| F | 70 | 2 |
| F | 73 | 4 |
| M | 55 | 9 |
| M | 65 | 3 |
| M | 61 | 7 |
| M | 59 | 1 |
| F | 75 | 4 |
| M | 64 | 2 |
3.6 (Motor Trend Car Road Tests)
We extracted 32 observation data from the 1974 Motor Trend US magazine, which comprised fuel consumption
and 10 aspects of automobile design and performance. The data have 11 variables as follows.
| V1 | mpg | Miles/(US) per gallon |
| V2 | cyl | Number of cylinders |
| V3 | disp | Displacement (cu.in.) |
| V4 | hp | Gross horsepower |
| V5 | drat | Rear axle ratio |
| V6 | wt | Weight (1000 lbs) |
| V7 | qsec | 1/4 mile time |
| V8 | vs | Engine (0 = V-shaped, 1 = straight) |
| V9 | am | Transmission (0 = automatic, 1 = manual) |
| V10 | gear | Number of forward gears |
| V11 | carb | Number of carburetors |
(Source: Henderson and Velleman (1981), Building multiple regression models interactively. Biometrics, 37, 391–411.)
This data are saved at the following location of 『eStat』.
[Ex] ⇨ DataScience ⇨ Mtcars.csv
3.6 Data collected by selecting 12 sub-areas and 5 different variables from a city in the United States are as follows. The five variables are regional population (Population), years of education (School), total employment (Employment), number of professional services (Service), and housing prices (House). Examine socioeconomic damage through principal component analysis.
| Population | School | Employment | Service | House |
|---|---|---|---|---|
| 5700 | 12.8 | 2500 | 270 | 25000 |
| 3400 | 8.8 | 1000 | 10 | 9000 |
| 4000 | 12.8 | 1600 | 140 | 25000 |
| 1200 | 11.4 | 400 | 10 | 16000 |
| 9900 | 12.5 | 3400 | 180 | 18000 |
| 9600 | 9.6 | 3300 | 80 | 12000 |
| 1000 | 10.9 | 600 | 10 | 10000 |
| 3800 | 13.6 | 1700 | 140 | 25000 |
| 8200 | 8.3 | 2600 | 60 | 12000 |
| 9100 | 11.5 | 3300 | 60 | 14000 |
| 9600 | 13.7 | 3600 | 390 | 25000 |
| 9400 | 11.4 | 4000 | 100 | 13000 |