Chapter 5. Estimation, testing hypothesis, and regression analysis
[presentation] [book]
- 5.1 Sampling distribution and estimation
- 5.1.1 Sampling distribution of sample means
- 5.1.2 Estimation of a population mean
- 5.2 Testing hypothesis for a population mean
- 5.3 Testing hypothesis for two populations means
- 5.4 Testing hypothesis for several population means: Analysis of variance
- 5.5 Regression analysis
- 5.5.1 Correlation analysis
- 5.5.2 Simple linear regression
- 5.5.3 Multiple linear regression
- 5.6 R and Python practice
- 5.7 Exercise
CHAPTER OBJECTIVES
5.1 Sampling distribution and estimation
5.1.1 Sampling distribution of sample means
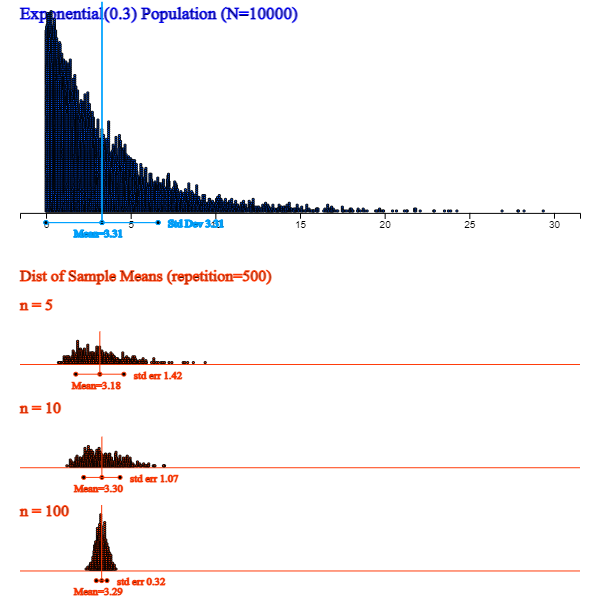
If a population is a normal distribution \( N(μ, σ^2 ) \), the distribution of all possible sample means is exactly a normal distribution \( N(μ, \frac {σ^2 }{n} ) \). If a population is not a normal distribution but the sample size is large enough, the distribution of all possible sample means is approximately a normal distribution such as \( N(μ, \frac {σ^2 }{n} ) \). We call this the central limit theorem, which is a key theory underlying modern statistics. Theoretical proof of this theorem is beyond the scope of this book; please refer to any book on mathematical statistics.
If a population has an infinite elements with a mean μ and variance \( σ^2 \), then, if the sample size is large enough, the distribution of all possible sample means is an approximately normal distribution \( N(μ, \frac {σ^2 }{n} ) \). We can summarize specifically the central limit theorem as follows.
(i.e., \(\small μ_{\overline X} = μ \) )
(i.e., \(\small σ_{\overline X}^2 = \frac {σ^2}{n} \) )
The above facts can be briefly written as \(\small \overline {X} \sim N(μ, \frac {σ^2}{n} ) \).
<Figure 5.1.1> shows a simulation using 『eStatU』 in case a population is skewed from its mean. The distribution of all possible sample means is closer to normal as the sample size increases.
5.1.2 Estimation of a population mean
The value of an observed sample mean is called a point estimate of the population mean. In general, the sample statistic used to estimate a population parameter must have good characteristics to be accurate. The sample mean has all the good characteristics to estimate the population mean, and the sample variance also has all the good characteristics to estimate the population variance.
In contrast to the point estimate for a population mean, estimating the population mean using an interval
is called an interval estimation.
If a population follows a normal distribution with the mean μ and variance \(σ^2 \),
the distribution of all possible sample means follows a normal distribution with the mean μ and variance \(\frac {σ^2}{n} \),
so the probability that one sample mean will be included in the interval
\( [\, μ - z_{\alpha / 2} \times \frac {σ}{\sqrt{n}} ,\; μ + z_{\alpha / 2} \times \frac {σ}{\sqrt{n}} \,]\)
is \(\small 1 -\alpha \) as follows.
$$\small
P(\mu - z_{\alpha / 2} \times \frac {σ}{\sqrt{n}} < \overline X < \mu + z_{\alpha / 2} \times \frac {σ}{\sqrt{n}} ) = 1 - \alpha
$$
We can rewrite this formula as follows.
$$\small
P(\overline X - z_{\alpha / 2} \times \frac {σ}{\sqrt{n}} < \mu < \overline X + z_{\alpha / 2} \times \frac {σ}{\sqrt{n}} ) = 1 - \alpha
$$
Assuming σ is known, the meaning of the above formula is that 95% of intervals obtained by applying the formula
\(\small [ \overline {X} - z_{\alpha / 2} \times \frac {σ}{\sqrt{n}}, \overline {X} + z_{\alpha / 2} \times \frac {σ}{\sqrt{n}} ] \)
for all possible sample means include the population mean. The formula of this interval is referred to as
the 100(1- \(\alpha \))% confidence interval of the population mean.
$$\small
\left[ \overline {X} - z_{\alpha / 2} \times \frac {σ}{\sqrt{n}}, \overline {X} + z_{\alpha / 2} \times \frac {σ}{\sqrt{n}} \right]
$$
100(1-α)% here is called a confidence level, which refers to the probability of intervals that will include
the population mean among all possible intervals calculated by the confidence interval formula. Usually, we use 0.01 or 0.05 for α.
\( z_{α} \) is the upper α percentile of the standard normal distribution.
In other words, if \(Z\) is the random variable that follows the standard normal distribution,
the probability that \(Z\) is greater than \( z_{α} \) is α, i.e.,
$$
P(Z > z_{α} ) = α
$$
For example, \( z_{0.025;} \) = 1.96, \( z_{0.05} \) = 1.645, \( z_{0.01} \) = 2.326, and \( z_{0.005} \) = 2.575.
The following simulation shows the 95% confidence intervals for the population mean by extracting 100 sets of samples with the sample size \(n\) = 20 from a population of 10,000 numbers which follow the standard normal distribution N(0,1). In this case, 96 of the 100 confidence intervals contain the population mean 0. This result might be different on your computer because the program uses a random number generator, which depends on the computer. Whenever we repeat these experiments, the result may also vary slightly.
Answer
\( \qquad \small z_{α/2} = z_{0.05/2} = 1.96 \)
\( \qquad \small \left[ \overline X - z_{\alpha/2} \frac {\sigma} {\sqrt{n}} ,\; \overline X + z_{\alpha/2} \frac {\sigma} {\sqrt{n}} \right] \)
\( \qquad \small ⇔ [ 275 - 1.96 \frac{5}{10},\; 275 + 1.96 \frac{5}{10} ] \)
\( \qquad \small ⇔ [274.02,\; 275.98] \)
\( \qquad \small z_{α/2} = z_{0.01/2} = 2.575 \)
\( \qquad \small [ 275 - 2.575 \frac{5}{10},\; 275 + 2.575 \frac{5}{10} ] \)
\( \qquad \small ⇔ [273.71,\; 276.29] \)
\( \qquad \small ⇔ [ 275 - 1.96 \frac{5}{20},\; 275 + 1.96 \frac{5}{20} ] \)
\( \qquad \small ⇔ [274.51,\; 275.49] \)
Interval estimation of a population mean – Unknown population variance
The shape of the \(t\) distribution is symmetrical about zero (y axis), similar to the standard normal distribution, but it has a tail that is flat and longer than the standard normal distribution. <Figure 5.1.2> shows the standard normal distribution N(0,1), and \(t\) distribution with 3 degrees of freedom simultaneously using the \(t\) distribution module of 『eStatU』.
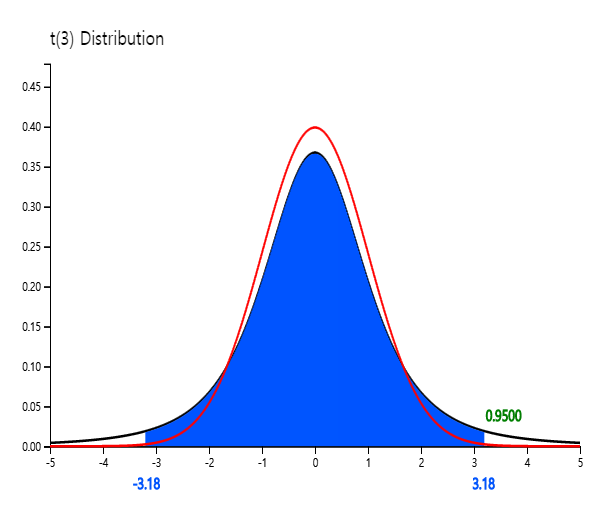
The \(t\) distribution is closer to the standard normal distribution as degrees of freedom increase above 100, which is why a confidence interval can be obtained approximately using the standard normal distribution if the sample size is greater than 100. Denote \(t_{n:\,α}\) as the 100\(\times\)α% percentile from the right tail of the \(t\) distribution with \(n\) degrees of freedom. For example, \(t_{7:\,0.05}\) is the 5% percentile of the \(t\) distribution from the right tail and its value is 1.895 as <Figure 5.1.3>. In the standard normal distribution, this value was 1.645. Since the \(t\) distribution is symmetrical, \(t_{n:\,1-α} = - t_{n:\,α}\). To find a percentile value from the right tail of the \(t_{7}\) distribution using 『eStatU』, click on '\(t\) distribution' in the main menu of 『eStatU』 and then set the degree of freedom (df) to 7, and set the probability value in the sixth option below the \(t\) distribution graph to 0.05, then \(t_{7:\,0.05}\) = 1.895 will appear.
Assume that a population follows a normal distribution, and consider an interval estimation of the population mean in case of the unknown population variance. If \( X_1 , X_2 , ... , X_n \) is a random sample of size \(n\) from the population, then it can be shown that the distribution of \( \frac {\overline X -\mu}{S/\sqrt{n}} \), where σ is replaced with S, is the \(t\) distribution with \( n-1 \) degrees of freedom. $$\small \frac {\overline X -\mu}{\frac{S}{\sqrt{n}}} \sim t_{n-1} $$ Hence, the probability of the following interval is (1 - α). $$\small P \left( -t_{n-1;\;\alpha/2} < \frac {\overline{X} - \mu } {\frac{S}{\sqrt{n}}} < t_{n-1:\;\alpha/2} \right) = 1 - \alpha $$ The above formula can be summarized as the confidence interval for the population mean when the population variance is unknown. $$\small \left[\; \overline X - t_{n-1:\;\alpha/2} \frac {S} {\sqrt{n}} ,\; \overline X + t_{n-1:\;\alpha/2} \frac {S} {\sqrt{n}} \; \right] $$ where \(n\) is the sample size and \(\small S\) is the sample standard deviation.
Answer
Since we do not know the population variance, we should use the \(t\) distribution for interval estimation of the population mean. Since \( t_{n-1:\;\alpha/2} = t_{25-1:\;0.05/2} = t_{25-1:\;0.025} = 2.0639 \), the 95% confidence interval of the population mean is as follows. $$ \small \begin{multline} \shoveleft \left[ \overline X - t_{n-1:\;\alpha/2} \frac {S} {\sqrt{n}} , \overline X + t_{n-1:\;\alpha/2} \frac {S} {\sqrt{n}} \right] \\ \shoveleft ⇔ [ 275 - 2.0639(5/5) , 275 + 2.0639(5/5) ] \\ \shoveleft ⇔ [ 272.9361, 277.0639 ] \end{multline} $$ Note that the smaller the sample size, the wider the interval width.
171 172 185 169 175 177 174 179 168 173
Answer
Click [Estimation : μ Confidence Interval] on the menu of 『eStatU』 and enter data at the [Sample Data] box. Then the confidence intervals [170.68, 177.92] are calculated using the \(t_9\) distribution. In this 『eStatU』 module, confidence intervals can also be obtained by entering the sample sizes, sample mean, and sample variance without entering data.
[ ]
In this module of 『eStatU』, a simulation experiment to investigate the size of the confidence interval can be done by changing the sample size \(n\) and the confidence level 1 - α. If you increase \(n\), the interval size becomes narrower. If you increase 1 - α, the interval size becomes wider.
5.2 Testing hypothesis for a population mean
The testing hypothesis is an answer to the above questions (hypothesis). The testing hypothesis is a statistical decision-making method using samples, which is used to compare two hypotheses about the population parameter. This section discusses the test of the population mean, which is frequently used in applications. The following example explains the theory of the testing hypothesis about a single population mean.
Answer
A statistical approach to the question of this issue is first to make two assumptions about the different arguments for the population mean μ . Namely, $$ \small \begin{multline} \shoveleft H_0 : μ = 1500 \\ \shoveleft H_1 : μ = 1600 \end{multline} $$ \(\small H_0\) is called a null hypothesis and \(\small H_1\) is an alternative hypothesis. In most cases, the null hypothesis is defined as an ‘existing known fact’ and the alternative hypothesis is defined as ‘new facts or changes in current beliefs’. So when choosing between two hypotheses, the basic idea of testing a hypothesis is 'unless there is a significant reason, we accept the null hypothesis (current fact) without choosing the alternative hypothesis (the fact of the matter). This idea of testing a hypothesis is referred to as ‘conservative decision making’.
A common sense for choosing between two hypotheses is 'which population mean of two hypotheses is closer in the distance to the sample mean'. Based on this common sense, which uses the concept of distance, the sample mean of 1555 is closer to \(\small H_1 : μ = 1600\), so we choose the alternative hypothesis. However, a statistical testing hypothesis makes a decision using the sampling distribution of \(\small \overline X\) to select a critical value \(C\) and to make a decision rule as follows.
\( \small \qquad \text { ‘If \(\overline X\) is smaller than C, then the null hypothesis \(H_0\) will be chosen, else reject \(H_0\)’} \)
The area of {\(\small \overline X ≤ C\)} is called an acceptance region of \(\small H_0\) and the area {\(\small \overline X > C\)} is called a rejection region of \(\small H_0\) (<Figure 5.2.1>).

If this decision rule chooses a hypothesis, there are always two possible errors. One is a Type 1 Error which accepts \(\small H_1\) when \(\small H_0\) is true, the other is a Type 2 Error which accept \(\small H_0\) when \(\small H_1\) is true. We can summarize these errors as in Table 5.2.1.
| Table 5.2.1 Two types of errors in testing hypothesis | ||
|---|---|---|
| Actual \(\small H_0\) is true |
Actual \(\small H_1\) is true |
|
| Decision : \(\small H_0\) is true | Correct | Type 2 Error |
| Decision : \(\small H_1\) is true | Type 1 Error | Correct |
If you try to reduce one type of error when the sample size is fixed, the other type of error will increase. That is why we came up with a conservative decision-making method that defines the null hypothesis \(\small H_0\) as 'past or present facts' and 'accept the null hypothesis unless there is significant evidence for the alternative hypothesis.' In this conservative way, we try to reduce the type 1 error as much as possible that selects \(\small H_1\) when \(\small H_0\) is true, which would be more risky than the type 2 error. The testing hypothesis determines the tolerance for the probability of the type 1 error, usually 5% or 1% for rigorous tests, and uses the selection criteria that satisfy this limitation. The tolerance for the probability that this type 1 error will occur is called the significance level and denoted as α. The probability of the type 2 error is denoted as β.
If the significance level is established, the decision rule for the two hypotheses can be tested using the sampling distribution of all possible sample means. <Figure 5.2.2> shows two population distributions of two hypotheses and their sampling distributions of all possible sample means in each hypothesis.
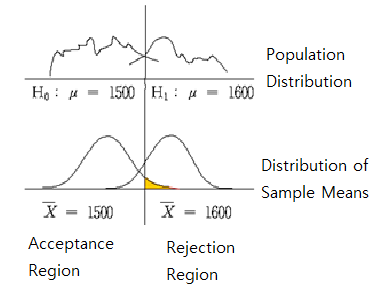
The sampling distribution of all possible sample means, which corresponds to the population of the null hypothesis \(\small H_0\) : μ = 1500, is approximately normal \(\small N(1500,200^2 )\) by the central limit theorem. The sampling distribution of all possible sample means, which corresponds to the population of the alternative hypothesis \(\small H_1\) : μ = 1600, is approximately normal \(\small N(1600,200^2 )\). The population standard deviation for each population is assumed to be 200 from historical data. Then, the decision rule becomes as follows.
\( \small \qquad \text {‘If \(\overline X ≤ C\), then accept \(H_{0}\), else accept \(H_{1}\) (i.e. reject \(H_{0}\) )’} \)
In Figure 5.2.2, the shaded area represents the probability of the type 1 error. If we set the significance level, which is the tolerance level of the type 1 error, is 5%, i.e., \(\small P(\overline X ≤ C) = 0.95\), \(C\) can be calculated by finding the percentile of the normal distribution \(\small N(1500,\frac{200^2}{30})\) as follows.
\( \small \qquad 1500+1.645 \frac{200}{\sqrt 30 } = 1560.06 \)
Therefore, the decision rule can be written as follows.
\( \small \qquad \text {‘If \(\overline X\) ≤ 1560.06, then accept \(H_0 \), else reject \(H_0\) (accept \(H_1\) ).’} \)
In this problem, the observed sample mean of the random variable \(\small \overline X\) is \(\small \overline x\)= 1555 and \(\small H_0 \) is accepted. In other words, the hypothesis of \(\small H_0 \) : μ = 1500 is judged to be correct, which contradicts the result of common sense criteria that \(\small \overline x\) = 1555 is closer to \(\small H_1 \) : μ = 1600 than \(\small H_0 \) : μ = 1500. We can interpret that the sample mean of 1555 is insufficient evidence to reject the null hypothesis using a conservative decision-making method.
The above decision rule is often written as follows, emphasizing that it results from a conservative decision-making method.
\( \small \qquad \text {‘If \(\overline X\) ≤ 1560.06, then do not reject \(H_0\), else reject \(H_0 \).’} \)
In addition, this decision rule can be written for calculation purposes as follows.
\( \small \qquad \text {‘If \(\frac{\overline X - 1500}{\frac {200}{\sqrt{30}}}\) ≤ 1.645, then accept \(H_0\) , else reject \(H_0\).’} \)
In this case, since \(\small\overline x\) = 1555, \(\frac{1555 - 1500}{\frac {200}{\sqrt{30}}}\) = 1.506, and it is less than 1.645. Therefore, we accept \(\small H_0\).
| 1) \(\quad H_1 : \mu \gt \mu_0\) | 2) \(\quad H_1 : \mu \lt \mu_0\) | 3) \(\quad H_1 : \mu \ne \mu_0\) |
In [Example 5.2.1], if the sample mean is either 1555 or 1540, we cannot reject the null hypothesis, but the degrees of evidence that the null hypothesis is not rejected are different. The degree of evidence that the null hypothesis is not rejected is measured by calculating the probability of the type 1 error when the observed sample mean value is considered as the critical value for decision, which is called the \(p\)-value. That is, the \(p\)-value indicates where the observed sample mean is located among all possible sample means by considering the location of the alternative hypothesis. In [Example 5.2.1], the \(p\)-value for \(\small\overline X\) = 1540 is the probability of sample means which is greater than \(\small\overline X\) = 1540 using \(N(1500, \frac{200^2}{30} )\) as follows. $$ \small p\text{-value} = P( \overline X > 1540) = P(\frac{\overline X - 1500}{\frac{200}{\sqrt{30}}} ) = 0.0660 $$ The higher the \(p\)-value, the stronger the reason for not being rejected. If \(H_0\) is rejected, the smaller the \(p\)-value, the stronger the grounds for rejection. Therefore, if the \(p\)-value is less than the significance level the analyst decided, then \(H_0\) is rejected because it means that the sample mean is in the rejection region. Statistical packages provide this \(p\)-value. The decision rule using \(p\)-value is as follows.
'If \(p\)-value < α, then \(H_0\) is rejected, else \(H_0\) is accepted.'
If the population standard deviation, σ, is unknown and the population follows a normal distribution, the test statistic $$\small \frac {\overline X - \mu_0}{ \frac {S}{\sqrt{n}} } $$ is a \(t\) distribution with \((n-1)\) degrees of freedom. If the population standard deviation is unknown, the decision rule for each type of three alternative hypothesis are summarized in Table 5.2.2 where α is the significance level.
| Table 5.2.2 Testing hypothesis for a population mean - unknown σ case | |
|---|---|
| Type of Hypothesis | Decision Rule |
| 1) \( \; H_0 : \mu = \mu_0 \) \(\quad\,\, H_1 : \mu > \mu_0 \) |
If \(\small \frac {\overline X - \mu_0}{ \frac {S}{\sqrt{n}} } > t_{n-1: \; α} \), then reject \( H_0 \) |
| 2) \( \; H_0 : \mu = \mu_0 \) \(\quad\,\, H_1 : \mu < \mu_0 \) |
If \(\small \frac {\overline X - \mu_0}{ \frac {S}{\sqrt{n}} } < - t_{n-1: \; α} \), then reject \( H_0 \) |
| 3) \( \; H_0 : \mu = \mu_0 \) \(\quad\,\, H_1 : \mu \ne \mu_0 \) |
If \(\small \left | \frac {\overline X - \mu_0}{ \frac {S}{\sqrt{n}} } \right | > t_{n-1; \; α/2} \), then reject \( H_0 \) |
| Note: Assume that the population is a normal distribution. The \(\small H_0\) of 1) can be written as \(\small H_0 : \mu \le \mu_0 \) , 2) as \(\small H_0 : \mu \ge \mu_0 \) |
|
Answer
Since the population standard deviation is unknown and the sample size is small, the decision rule is as follows. $$ \small \begin{multline} \shoveleft \text{'If } \frac {\overline X - \mu_0} {\frac {S}{\sqrt{n}} } > t_{n-1: \; α} , \text{ then reject } H_0 \text{ else accept } H_0 ’ \\ \shoveleft \text{'If } \frac {253 - 250}{ \frac {10}{\sqrt{16}} } > t_{16:\; 0.01} , \text{ then reject } H_0 \text{ else accept } H_0 ’ \\ \end{multline} $$ Since the value of test statistic is \( \frac {253 - 250}{ \frac {10}{\sqrt{16}} } = 1.2 \), and \(t_{15: \; 0.01} = 2.602\) , we accept \(\small H_0\). Note that the decision rule can be written as follows.
\( \small \qquad \qquad\text{'If } \overline X > 250 + 2.602 \frac {10}{\sqrt{16}} , \text{ then reject } H_0 \text{ else accept } H_0 ’ \\ \)
In 『eStatU』 menu, select [Testing Hypothesis μ], enter 250 at the box on [Hypothesis] and select the alternative hypotheses as the right test. Check [Test Type] as t test and enter &alpha = 0.01. At the [Sample Statistics], enter sample size 16, sample mean 253, and sample variance \(10^2 = 100\). If you click the [Execute] button, the confidence Interval for μ is calculated, and the testing result will appear as in <Figure 5.2.3>.
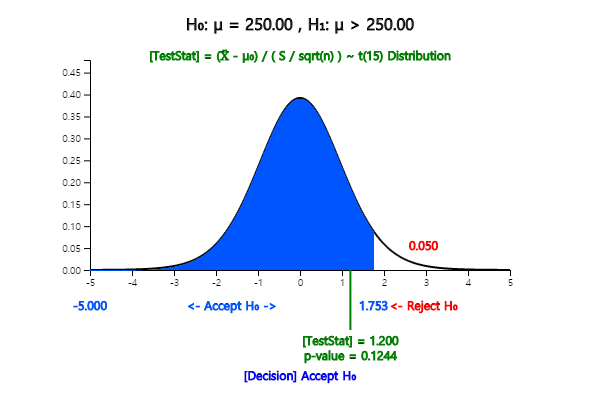
Since the \(p\)-value is the probability that \(t_{15}\) is greater than the test statistics 1.200, the \(p\)-value is 0.124 using the module of \(t\) distribution in 『eStatU』.
[Testing Hypothesis : Population Mean μ ]
Based on this data, is the average weight of employees working in the shipping department 160 or greater than 160? Use the significance level of 5%.
5.3 Testing hypothesis for two populations means
Generally, testing hypothesis for two populations means can be divided into three types, depending on the type of alternative hypothesis. $$ \small \begin{multline} \shoveleft 1)\quad H_0 : \mu_1 - \mu_2 = D_0 \qquad H_1 : \mu_1 - \mu_2 \gt D_0 \\ \shoveleft 2)\quad H_0 : \mu_1 - \mu_2 = D_0 \qquad H_1 : \mu_1 - \mu_2 \lt D_0 \\ \shoveleft 3)\quad H_0 : \mu_1 - \mu_2 = D_0 \qquad H_1 : \mu_1 - \mu_2 \ne D_0 \\ \end{multline} $$ Here \(\small D_0\) is the value for the difference in population means to be tested. When samples are selected independently from two populations, the estimator of the difference of two population means, \(\small \mu_1 - \mu_2\), is the difference of sample means, \(\small {\overline x}_1 - {\overline x}_2\). If two populations follow normal distributions and their variances can be assumed to be the same, the testing hypothesis for the difference between the two populations means uses the following statistic. $$ \small \frac { ({\overline x}_1 - {\overline x}_2 ) - D_0 }{\sqrt{\frac{s^2_p}{n_1} +\frac{s^2_p}{n_2} } } \qquad \text{where } s^2_p = \frac{(n_1 -1 )s^2_1 + (n_2 -1)s^2_2}{n_1 + n_2 -2} $$ The test statistic follows a \(t\)-distribution with \(n_1 + n_2 -2\) degrees of freedom. The decision rule for testing the difference between the two populations' means is as follows.
| Table 5.3.1 Testing hypothesis of two populations means | |
|---|---|
| Type of Hypothesis | Decision Rule |
| 1) \( \; H_0 : \mu_1 - \mu_2 = D_0 \) \(\quad\,\, H_1 : \mu_1 - \mu_2 > D_0 \) |
If \(\small \frac { ({\overline x}_1 - {\overline x}_2 ) - D_0 }{\sqrt{\frac{s^2_p}{n_1} +\frac{s^2_p}{n_2} } } > t_{n_1 + n_2 -2; \; α} \), then reject \( H_0 \), else accept \( H_0 \) |
| 2) \( \; H_0 : \mu_1 - \mu_2 = D_0 \) \(\quad\,\, H_1 : \mu_1 - \mu_2 < D_0 \) |
If \(\small \frac { ({\overline x}_1 - {\overline x}_2 ) - D_0 }{\sqrt{\frac{s^2_p}{n_1} +\frac{s^2_p}{n_2} } } < - t_{n_1 + n_2 -2; \; α} \), then reject \( H_0 \), else accept \( H_0 \) |
| 3) \( \; H_0 : \mu_1 - \mu_2 = D_0 \) \(\quad\,\, H_1 : \mu_1 - \mu_2 \ne D_0 \) |
If \(\small \left | \frac { ({\overline x}_1 - {\overline x}_2 ) - D_0 }{\sqrt{\frac{s^2_p}{n_1} +\frac{s^2_p}{n_2} } } \right | > t_{n_1 + n_2 -2; \;α/2} \), then reject \( H_0 \), else accept \( H_0 \) |
| Note: Assume independent samples, normal populations, population variances are equal. If sample sizes are large enough (\(\small n_1 > 30, n_2 >30 \)), \(t\)-distribution is approximately close to the standard normal distribution and the decision rule may use the standard normal distribution. |
|
1) Find a 99% confidence interval for the difference between two population means.
2) Test whether the two machines' cookie bag weights are different. Use α = 0.01.
3) Check the test result using 『eStatU』.
Answer
1) We can summarize the sample information in this example as follows. $$ \small \begin{multline} \shoveleft n_1 = 15,\quad \overline x_1 = 275,\quad s_1 = 12 \\ \shoveleft n_2 = 14,\quad \overline x_2 = 269,\quad s_2 = 10 \\ \end{multline} $$ Therefore, the pooled variance of two samples is as follows. $$ \small \begin{multline} \shoveleft s^2_p = \frac{(n_1 -1 )s^2_1 + (n_2 -1)s^2_2}{n_1 + n_2 -2} = \frac{(15 - 1 ) 12^2 + (14 - 1) 10^2}{15 + 14 -2} = 122.815 \\ \end{multline} $$ Since the t-value for 99% confidence interval is \(\small t_{15 + 14 -2;\; 0.01/2} = t_{27:\; 0.005} = 2.7707\), the 99% confidence interval is as follows. $$ \small \begin{multline} \left[\; (\overline X_1 - \overline X_2 ) - t_{n_1 + n_2 - 2: \;\alpha/2} \sqrt { \frac{S^2_p}{n_1} + \frac{S^2_p}{n_2} },\; (\overline X_1 - \overline X_2 ) + t_{n_1 + n_2 -2:\;\alpha/2} \sqrt { \frac{S^2_p}{n_1} + \frac{S^2_p}{n_2} } \;\right] \end{multline} $$ $$\small \begin{multline} \left[\; (275 - 269) - 2.7707 \sqrt { \frac{122.815}{15} + \frac{122.815}{14} },\; (275 - 269) + 2.7707 \sqrt { \frac{122.815}{15} + \frac{122.815}{14} } \;\right] \\ \end{multline} $$ $$\small \begin{multline} \left[\; -5.410, \; 17.410 \; \right ] \end{multline} $$
2) The hypothesis of this problem is \(\small H_0 : \mu_1 = \mu_2 ,\, H_1 : \mu_1 \ne \mu_2 \). Hence, the decision rule is as follows. $$ \small \begin{multline} \shoveleft '\text{If } \left | \frac { ({\overline x}_1 - {\overline x}_2 ) - D_0 }{\sqrt{\frac{s^2_p}{n_1} +\frac{s^2_p}{n_2} } } \right | > t_{n_1 + n_2 -2;\, α/2} , \text{ then reject } H_0 ’ \\ \end{multline} $$ \(\small D_0 = 0\) in this exaample. The calculation of the test statistic is as follows. $$ \small \begin{multline} \shoveleft \left | \frac {275 - 269} { \sqrt{\frac{122.815}{15} +\frac{122.815}{14} } } \right | = 1.457 \\ \end{multline} $$ Since 1.457 < 2.7707, \(\small H_0\) can not be rejected.
3) In 『eStatU』 menu, select [Testing Hypothesis \(\mu_1 , \mu_2\)]. At the window shown in <Figure 5.3.1>, check the alternative hypotheses of not equal case at [Hypothesis], check the variance assumption of [Test Type] as the equal case, check the significance level of 1%, check the independent sample, and enter sample sizes \(n_1 , n_2\), sample means \(\small \overline x_1 , \overline x_2\), and sample variances as the following window. Click [Execute] button to see the confidence interval and result of the testing hypothesis.
[Testing Hypothesis : two populations Means μ1, μ2]
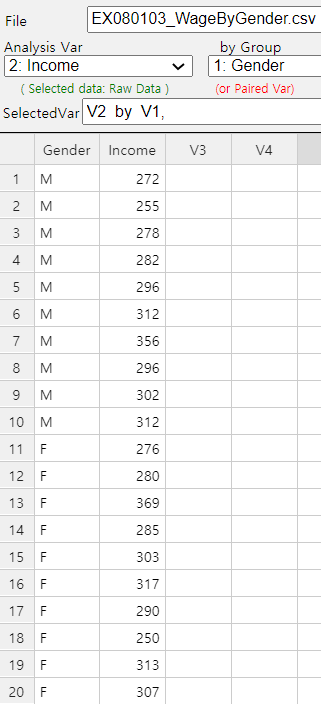
Random samples of 10 male and female college graduates this year showed their monthly wages as follows. (Unit 10,000 KRW)
Female 276 280 369 285 303 317 290 250 313 307
Ex ⇨ DataScience ⇨ WageByGender.csv.
Using 『eStat』, answer the following questions.
Answer
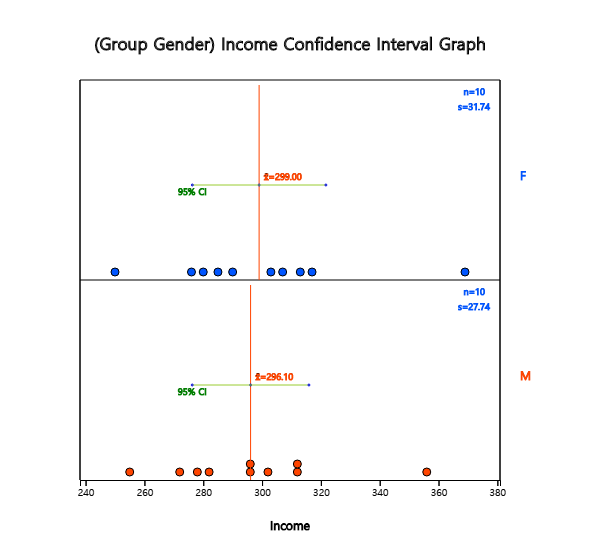
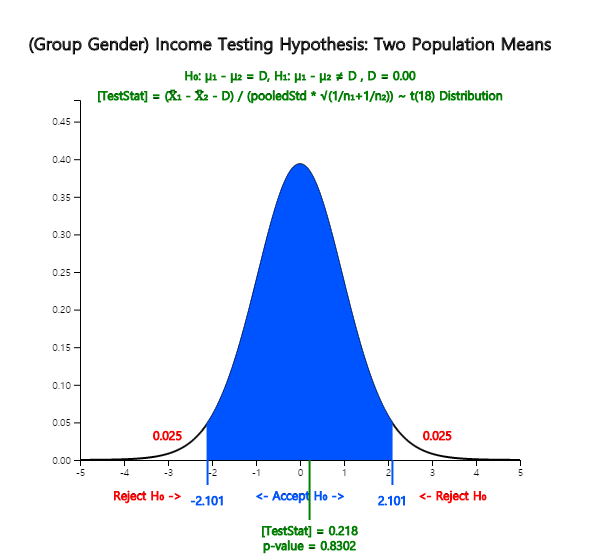
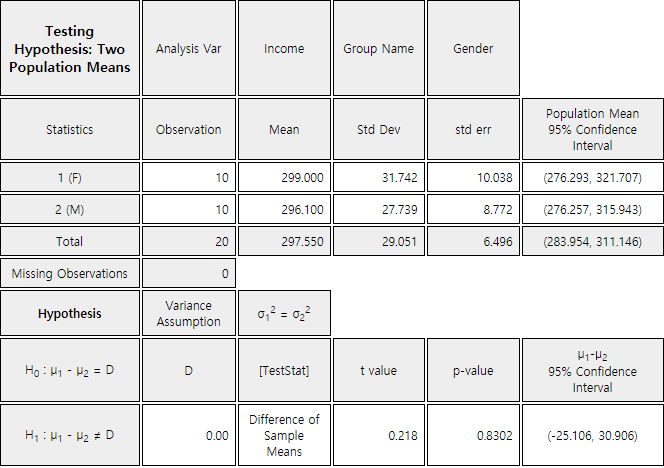
In the options window, as in <Figure 5.3.3> located below the Graph Area, enter the average difference \(\small D = 0\) for the desired test, select the variance assumption \(\sigma_1^2 = \sigma_2^2\), the 5% significance level and click the [t-test] button. Then, the graphical result of the testing hypothesis for two populations' means will be shown as in <Figure 5.3.4> and the test result as in <Figure 5.3.5>.

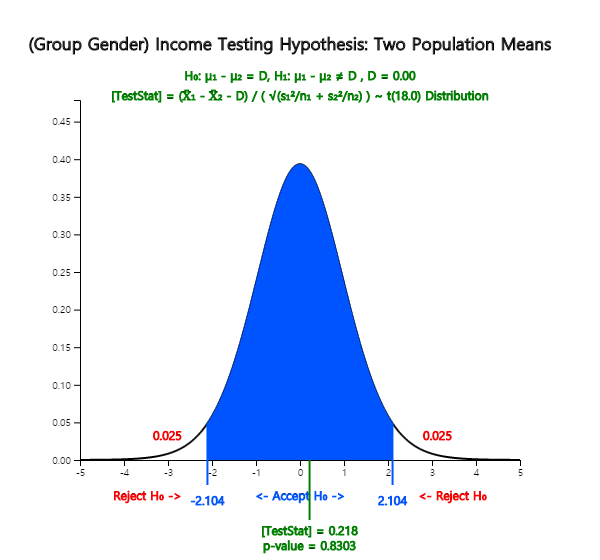
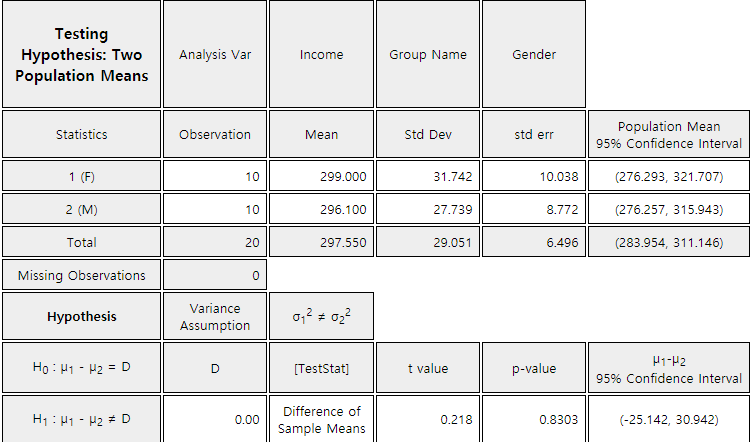
Oral cleanliness scores were examined for eight samples using the basic brushing method (coded 1) and seven samples using the rotation method (coded 2). The data are saved at the following location of 『eStat』.
5.4 Testing hypothesis for several population means: Analysis of variances
The group variable used to distinguish population groups, such as the grade or the rice, is called a factor. This section describes the one-way analysis of variance (ANOVA), which compares population means when there is a single factor. Let us take a look at the following example.
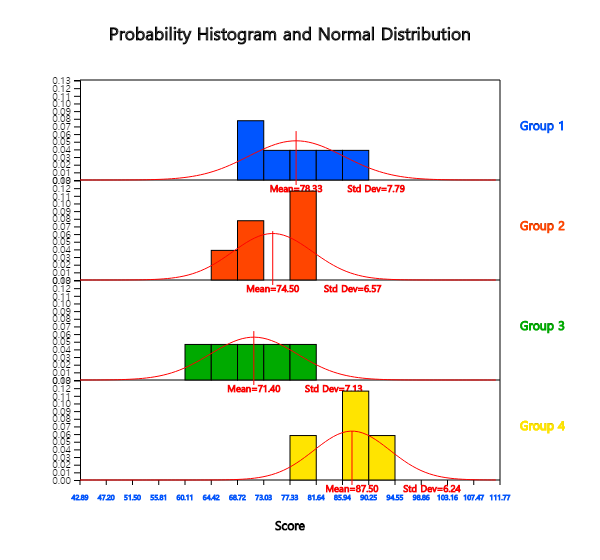
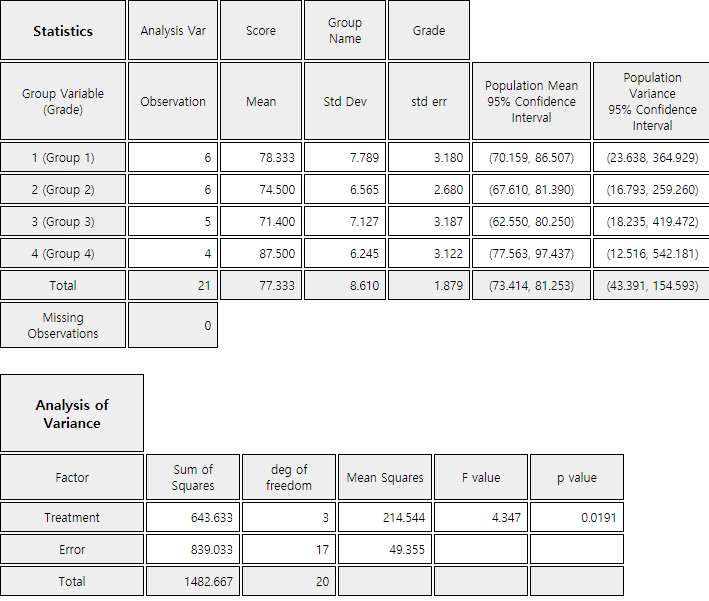
| Table 5.4.1 English Proficiency Score by Grade | |||||||
|---|---|---|---|---|---|---|---|
| Socre | Student 1 | Student 2 | Student 3 | Student 4 | Student 5 | Student 6 | Student Average |
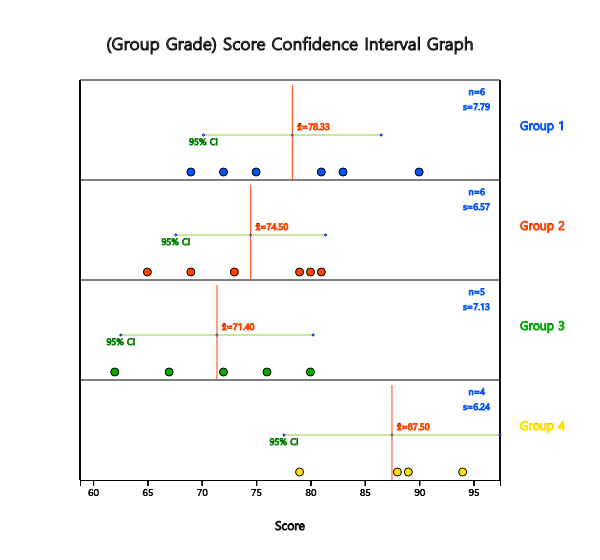
| Grade 1 | 81 | 75 | 69 | 90 | 72 | 83 | \({\overline y}_{1\cdot}\)=78.3 |
| Grade 2 | 65 | 80 | 73 | 79 | 81 | 69 | \({\overline y}_{2\cdot}\)=74.5 |
| Grade 3 | 72 | 67 | 62 | 76 | 80 | \({\overline y}_{3\cdot}\)=71.4 | |
| Grade 4 | 89 | 94 | 79 | 88 | \({\overline y}_{4\cdot}\)=87.5 | ||
[Ex] ⇨ DataScience ⇨ EnglishScoreByGrade.csv.
Answer
 |
|
<Figure 5.4.1> 『eStat』 data input for ANOVA |

\(\small \qquad + (65 -{\overline y}_{2 \cdot})^2 + (80 -{\overline y}_{2 \cdot})^2 + \cdots + (69 -{\overline y}_{2 \cdot})^2\)
\(\small \qquad + (72 -{\overline y}_{3 \cdot})^2 + (67 -{\overline y}_{3 \cdot})^2 + \cdots + (80 -{\overline y}_{3 \cdot})^2\)
\(\small \qquad + (89 -{\overline y}_{4 \cdot})^2 + (94 -{\overline y}_{4 \cdot})^2 + \cdots + (88 -{\overline y}_{4 \cdot})^2\)
\(\small = 839.033\)
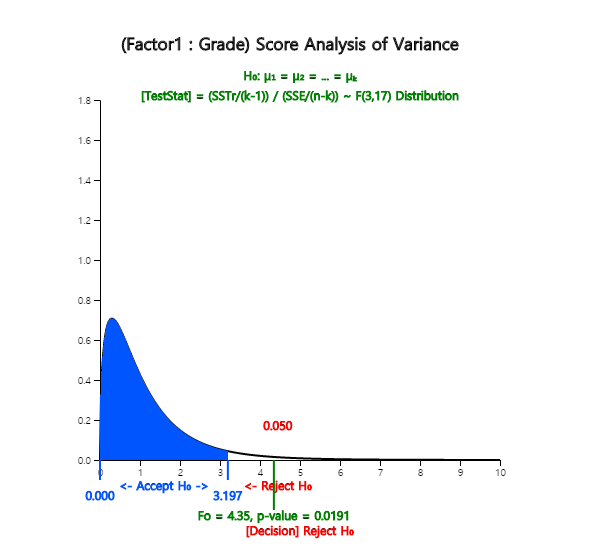
The calculated test statistic, which is the observed \(\small F\) value \(\small F_{0}\), using data of English scores for each grade is as follows.
| Factor | Sum of Squares | Degree of freedom | Mean Squares | F ratio |
|---|---|---|---|---|
| Treatment | SSTr = 643.633 | 4-1 | MSTr = \(\frac{643.633}{3}\) | \(F_0 = 4.347\) |
| Error | SSE = 839.033 | 21-4 | MSE = \(\frac{839.033}{17}\) | |
| Total | SST = 1482.666 | 20 |
The analysis of variance is also possible using 『eStatU』 as below. Entering the data as below, and clicking the [Execute] button will have the same result as in <Figure 5.4.5> and <Figure 5.4.6>.
[Testing Hypothesis : 3+ Population Means (ANOVA)]
| Table 5.4.2 Notation of the one-way ANOVA | ||
|---|---|---|
| Factor | Observed values of sample | Average |
| Level 1 | \(Y_{11} \; Y_{12}\; \cdots \;Y_{1n_1} \) | \(\overline Y_{1\cdot}\) |
| Level 2 | \(Y_{21} \; Y_{22}\; \cdots \;Y_{2n_2} \) | \(\overline Y_{2\cdot}\) |
| \(\cdots\) | \(\cdots\) | \(\cdots\) |
| Level k | \(Y_{k1} \; Y_{k2}\; \cdots \;Y_{kn_k} \) | \(\overline Y_{k\cdot}\) |
| Total | \( {\overline Y}_{\cdot \cdot} \) | |
Statistical model for the one-way analysis of variance is given as follows. $$ \begin{align} Y_{ij} &= \mu_i + \epsilon_{ij} \\ &= \mu + \alpha_i + \epsilon_{ij}, \;i=1,2,...,k; \;j=1,2,..., n_i \\ &\text{where}\;\; \epsilon_{ij} \backsim N(0, \sigma ^2) \end{align} $$ \(Y_{ij}\) represents the \(j^{th}\) observed value of the response variable for the \(i^{th}\) level of factor. The population mean of the \(i^{th}\) level, \(\mu_{i}\), is represented as \(\mu + \alpha_{i}\) where \(\mu\) is the mean of entire population and \(\alpha_{i}\) is the effect of \(i^{th}\) level for the response variable. \(\epsilon_{ij}\) denotes an error term of the \(j^{th}\) observation for the \(i^{th}\) level, and the all error terms are assumed independent of each other and follow the same normal distribution with the mean 0 and variance \(\sigma^{2}\). The error term \(\epsilon_{ij}\) is a random variable in the response variable due to reasons other than levels of the factor. For example, in the English score example, differences in English performance for each grade can be caused by other variables besides the variables of grade, such as individual study hours, gender and IQ. However, by assuming that these variations are relatively small compared to variations due to differences in grade, the error term can be interpreted as the sum of these various reasons. The hypothesis to test can be represented using \(\alpha_{i}\) instead of \(\mu_{i}\) as follows.
The analysis of variance table as Table 5.4.3 is used to test the hypothesis.
| Table 5.4.3 Analysis of variance table of the one-way ANOVA | ||||
|---|---|---|---|---|
| Factor | Sum of Squares | Degree of freedom | Mean Squares | F ratio |
| Treatment | SSTr | \(k-1\) | MSTr=\(\frac{SSTr}{k-1}\) | \(F_0 = \frac{MSTr}{MSE}\) |
| Error | SSE | \(n-k\) | MSE=\(\frac{SSE}{n-k}\) | |
| Total | SST | \(n-1\) | ||
| where \(\qquad n = \sum_{i=1}^{n} \; n_i\) | ||||
The sum of squared distances between observed values of the response variable and the mean of total observations is called the total sum of squares (SST).
SSTr = \(\sum_{i=1}^{k} \sum_{j=1}^{n_i} ( {\overline Y}_{i \cdot} - {\overline Y}_{\cdot \cdot} )^2 \;\) :
The sum of squared distances between the mean of each level and the mean of total observations is called the
treatment sum of squares (SSTr). It represents the variation between level means.
SSE = \(\sum_{i=1}^{k} \sum_{j=1}^{n_i} ( {Y}_{ij} - {\overline Y}_{i \cdot} )^2 \;\) :
The sum of squared distances between observations of the \(i^{th}\) level and the mean of the \(i^{th}\) level is referred to as
'within variation', and is called the error sum of squares (SSE).
Sum of squares: SST = SSTr + SSE
Degrees of freedom: \((n-1) = (k-1) + (n-k)\)
The sum of squares divided by the corresponding degrees of freedom is referred to as the mean squares, and Table
5.4.3 defines the treatment mean squares (MSTr) and error mean squares (MSE).
The treatment mean square implies the average variation between each level of the factor, and the error
mean square implies the average variation within observations in each level. Therefore, if MSTr is relatively
much larger than MSE, we can conclude that the population means of each level, \(\mu_i\), are not the same. So by what
criteria can you say it is relatively much larger?
The calculated \(F\) value, \(F_0\), in the last column of the ANOVA table represents the relative size of MSTr and MSE. If the assumptions of \(\epsilon_{ij}\) are satisfied, and if the null hypothesis \(\small H_0 : \alpha_1 = \alpha_2 = \cdots = \alpha_k \) = 0 is true, then the test statistic follows a \(F\) distribution with degrees of freedoms \(k-1\) and \(n-k\). $$ F_{0} = \frac { \frac{SSTr}{(k-1)} } { \frac{SSE}{(n-k)} } $$ Therefore, when the significance level is \(\alpha\) for a test, if the calculated value \(F_0\) is greater than the value of \(F_{k-1,n-k; α}\), then the null hypothesis is rejected. That is, it is determined that the population means of each factor level are different. (Note: 『eStat』 calculates this test's \(p\)-value. Hence, if the \(p\)-value is smaller than the significance level \(\alpha\), then reject the null hypothesis.)
Results from an experiment to compare yields (as measured by the dried weight of plants) obtained under a control (leveled ‘ctrl’) and two treatment conditions (leveled ‘trt1’ and ‘trt2’). The weight data with 30 observations on control and two treatments (‘crtl’, ‘trt1’, ‘trt2’), are saved at the following location of 『eStat』. Answer the following using 『eStat』 ,
5.5 Regression analysis
5.5.1 Correlation analysis
Null hypothesis: \(H_0 : \rho = 0\)
Test statistic: \(\quad t_0 = \sqrt{n-2} \frac{r}{\sqrt{1 - r^2 }}\) follows \(t\) distribution with \(n-2\) degrees of freedom
Rejection region of \(H_0\):
\( \qquad 1)\; H_1 : \rho < 0 : \;\;\) Reject if \(\; t_0 < -t_{n-2;\, α}\)
\( \qquad 2)\; H_1 : \rho > 0 : \;\;\) Reject if \(\; t_0 > t_{n-2;\, α}\)
\( \qquad 3)\; H_1 : \rho \ne 0 : \;\;\) Reject if \(\; |t_0 | > t_{n-2;\, α/2}\)
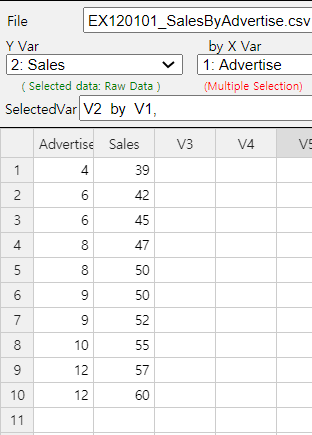
| Company | Advertise (X) | Sales (Y) |
|---|---|---|
| 1 | 4 | 39 |
| 2 | 6 | 42 |
| 3 | 6 | 45 |
| 4 | 8 | 47 |
| 5 | 8 | 50 |
| 6 | 9 | 50 |
| 7 | 9 | 52 |
| 8 | 10 | 55 |
| 9 | 12 | 57 |
| 10 | 12 | 60 |
Answer
Using 『eStat』 , enter data as shown in <Figure 5.5.1>. If you select the Sales as 'Y Var' and the Advertise 'by X Var' in the variable selection box that appears when you click the scatter plot icon on the main menu, the scatter plot will appear as shown in <Figure 5.5.2>. As we can expect, the scatter plot show that the more investments in advertising, the more sales increase, and not only that, the form of increase is linear.
|
|
|
|
<Figure 5.5.1> Data input in 『eStat』
|
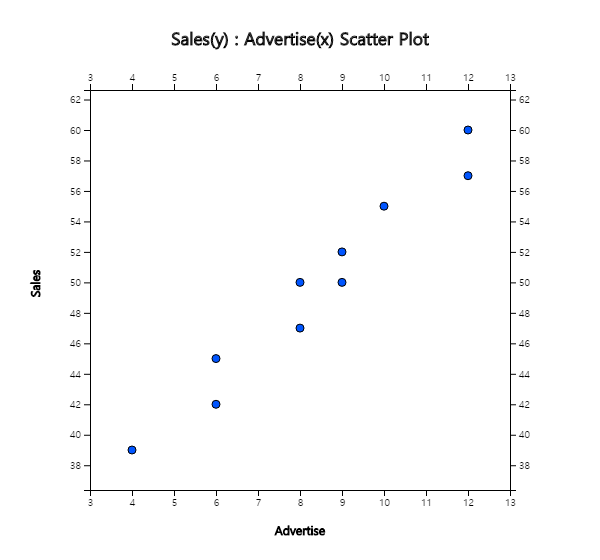
To calculate the sample covariance and correlation coefficient, it is convenient to make the following table. This table can also be used for calculations in regression analysis.
| Number | \(X\) | \(Y\) | \(X^2\) | \(Y^2\) | \(XY\) |
|---|---|---|---|---|---|
| 1 | 4 | 39 | 16 | 1521 | 156 |
| 2 | 6 | 42 | 36 | 1764 | 252 |
| 3 | 6 | 45 | 36 | 2025 | 270 |
| 4 | 8 | 47 | 64 | 2209 | 376 |
| 5 | 8 | 50 | 64 | 2500 | 400 |
| 6 | 9 | 50 | 81 | 2500 | 450 |
| 7 | 9 | 52 | 81 | 2704 | 468 |
| 8 | 10 | 55 | 100 | 3025 | 550 |
| 9 | 12 | 57 | 144 | 3249 | 684 |
| 10 | 12 | 60 | 144 | 3600 | 720 |
| Sum | 64 | 497 | 766 | 25097 | 4326 |
| Mean | 8.4 | 49.7 |
Terms which are necessary to calculate the covariance and correlation coefficient are as follows:
\(\small \quad SXX = \sum_{i=1}^{n} (X_i - \overline X )^{2} = \sum_{i=1}^{n} X_{i}^2 - n{\overline X}^{2} = 766 - 10×8.4^2 = 60.4 \)
\(\small \quad SYY = \sum_{i=1}^{n} (Y_i - \overline Y )^{2} = \sum_{i=1}^{n} Y_{i}^2 - n{\overline Y}^{2} = 25097 - 10×49.7^2 = 396.1 \)
\(\small \quad SXY = \sum_{i=1}^{n} (X_i - \overline X )(Y_i - \overline Y ) = \sum_{i=1}^{n} X_{i}Y_{i} - n{\overline X}{\overline Y} = 4326 - 10×8.4×49.7 = 151.2 \)
\(\small SXX, SYY, SXY \)represent the sum of squares of \(\small X\), the sum of squares of \(\small Y\), the sum of squares of \(\small XY\). Hence, the covariance and correlation coefficient are as follows:
\(\small \quad S_{XY} = \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \overline X )(Y_i - \overline Y ) = \frac{151.2}{10-1} = 16.8 \)
\(\small \quad r = \frac {\sum_{i=1}^{n} (X_i - \overline X )(Y_i - \overline Y )} { \sqrt{\sum_{i=1}^{n} (X_i - \overline X )^{2} \sum_{i=1}^{n} (Y_i - \overline Y )^{2} } } = \frac{151.2} { \sqrt{ 60.4 × 396.1 } } = 0.978 \)
This sample correlation coefficient is consistent with the scatter plot which shows a strong positive correlation of the two variables. The value of the test statistic \(t_0\) is as follows.
\(\qquad \small t_0 = \sqrt{10-2} \frac{0.978}{\sqrt{1 - 0.978^2 }}\) = 13.117
Since it is greater than \(t_{8;\; 0.025}\) = 2.306, \(\small H_0 : \rho = 0\) should be rejected.
The correlation analysis can be done using 『eStatU』 by following data input and clicking [Execute] button..
[]
| id | Mid-term X | Final Y |
|---|---|---|
| 1 | 92 | 87 |
| 2 | 65 | 71 |
| 3 | 75 | 75 |
| 4 | 83 | 84 |
| 5 | 95 | 93 |
| 6 | 87 | 82 |
| 7 | 96 | 98 |
| 8 | 53 | 42 |
| 9 | 77 | 82 |
| 10 | 68 | 60 |
5.5.2 Simple linear regression
In regression analysis, a mathematical model of the relation between variables is called a regression equation, and the variable affected by other related variables is called a dependent variable. The dependent variable is the variable we would like to describe, which is usually observed in response to other variables, so it is also called a response variable. In addition, variables that affect the dependent variable are called independent variables. The independent variable is also referred to as the explanatory variable because it is used to describe the dependent variable. In the previous example, if the objective is to analyze the change in sales amounts resulting from increases and decreases in advertising costs, the sales is a dependent variable, and the advertising cost is an independent variable. If the number of independent variables included in the regression equation is one, it is called a simple linear regression. If the number of independent variables is two or more, it is called a multiple linear regression, explained in section 5.5.3.
Simple linear regression analysis has only one independent variable, and the regression equation is as follows. $$ Y = f(X,\alpha,\beta) = \alpha + \beta X $$ In other words, the regression equation is represented by a linear equation of the independent variable, and \(\alpha\) and \(\beta\) are unknown parameters that represent the intercept and slope, respectively. The \(\alpha\) and \(\beta\) are called the regression coefficients. The above equation represents an unknown linear relationship between \(Y\) and \(X\) in population and is referred to as the population regression equation.
To estimate the regression coefficients \(\alpha\) and \(\beta\), observations of the dependent and independent variables are required, i.e., samples. In general, all of these observations are not located in a line. It is because, even if the \(Y\) and \(X\) have an exact linear relation, there may be a measurement error in the observations, or there may not be an exact linear relationship between \(Y\) and \(X\). Therefore, we can write the regression formula by considering these errors as follows. $$ Y_i = \alpha + \beta X_i + \epsilon_{i}, \quad i=1,2,...,n $$ Where \(i\) is the subscript representing the \(i^{th}\) observation, and \(\epsilon_i\) is the random variable indicating an error with a mean of zero and a variance \(\sigma^2\) which is independent of each other. The error \(\epsilon_i\) indicates that the observation \(Y_i\) is how far away from the population regression equation. The above equation includes unknown population parameters \(\alpha\), \(\beta\), and \(\sigma^2\) and is referred to as a population regression model.
If \(a\) and \(b\) are the estimated regression coefficients using samples, the fitted regression equation can be written as follows. It is referred to as the sample regression equation. $$ {\hat Y}_i = a + b X_i $$ In this expression, \({\hat Y}_i\) represents the estimated value of \(Y\) at \(X=X_i\) as predicted by the appropriate regression equation. These predicted values can not match the actual observed values of \(Y\), and differences between these values are called residuals and denoted as \(e_i\). $$ \text{residuals} \qquad e_i = Y_i - {\hat Y}_i , \quad i=1,2,...,n $$ The regression analysis makes assumptions about the unobservable error \(\epsilon_i\). Since the residuals \(e_i\) calculated using the sample values have similar characteristics as \(\epsilon_i\), they are used to investigate the validity of these assumptions.
A method of estimating regression coefficients so that the total sum of the squared errors occurring in each observation is minimized. i.e.,
$$ \text{Find} \; \alpha \; \text{and} \; \beta \; \text{which minimize} \quad \sum_{i=1}^{n} \epsilon_{i}^2 = \sum_{i=1}^{n} ( Y_i - \alpha - \beta X_i )^2 $$
$$ \begin{align} b &= \frac {\sum_{i=1}^{n} (X_i - \overline X ) (Y_i - \overline Y )} { \sum_{i=1}^{n} (X_i - \overline X )^2 } \\ a &= \overline Y - b \overline X \end{align} $$
However, it is not clear how small the residual standard error \(s\) is, although the smaller the value is, the better. In addition, the size of the value of \(s\) depends on the unit of \(Y\). A relative measure called the coefficient of determination is defined to eliminate this shortcoming. The coefficient of determination is the ratio of the variation described by the regression line over the total variation of observation \(Y_i\), so that it is a relative measure that can be used regardless of the type and unit of a variable. As in the analysis of variance in the previous section, the following partitions of the sum of squares and degrees of freedom are established in the regression analysis: $$ \begin{align} \text{Sum of squares:} \qquad \;\; SST \;=\; SSE \;+\; SSR \\ \text{Degrees of freedom:} \quad (n-1) = (n-2) + 1 \end{align} $$ Description of the above three sums of squares is as follows.
The total sum of squares indicating the total variation in observed values of \(\small Y\) is called the total sum of squares (\(\small SST\)). This \(\small SST\) has the degree of freedom, \(n-1\), and if \(\small SST\) is divided by the degree of freedom, it becomes the sample variance of \(\small Y_i\).
Error sum of squares : \( \small SSE = \sum_{i=1}^{n} ( Y_i - {\hat Y}_i )^2\)
The error sum of squares (\(\small SSE\)) of the residuals represents the unexplained variation of the
total variation of the \(\small Y\). Since the calculation of this sum of squares requires the estimation of
two parameters \(\alpha\) and \(\beta\), \(\small SSE\) has the degree of freedom \(n-2\).
This is the reason why, in the calculation of the sample variance of residuals \(s^2\), it was divided
by \(n-2\).
Regression sum of squares : \( \small SSR = \sum_{i=1}^{n} ( {\hat Y}_i - {\overline Y} )^2 \)
The regression sum of squares (\(\small SSR\)) indicates the variation explained by the regression line
among the total variation of \(\small Y\). This sum of squares has the degree of freedom of 1.
| Table 5.5.2 Analysis of variance table for simple linear regression | ||||
|---|---|---|---|---|
| Source | Sum of squares | Degrees of freedom | Mean Squares | F value |
| Regression | SSR | 1 | MSR =\(\frac{SSR}{1}\) | \(F_0 = \frac{MSR}{MSE}\) |
| Error | SSE | \(n-2\) | MSE = \(\frac{SSE}{n-2}\) | |
| Total | SST | \(n-1\) | ||
The parameter \(\beta\), the slope of the regression line, indicates the existence and extent of a linear relationship between the dependent and the independent variables. The inference for \(\beta\) can be summarized as follows. The test for hypotheses \(H_0 : \beta = 0\) is used to determine the independent variable describes the dependent variable significantly or not. The \(F\) test for the hypothesis \(H_0 : \beta = 0\) described in the ANOVA of regression is theoretically the same as in the test below.
Point estimate: \(\small \quad b = \frac {\sum_{i=1}^{n} (X_i - \overline X) (Y_i - \overline Y)} { \sum_{i=1}^{n} (X_i - \overline X)^2 } , \quad b \sim N(\beta, \frac{\sigma^2} {\sum_{i=1}^{n} (X_i - \overline X )^2 } ) \)
Standard error of estimate \(b\): \(\small \quad SE(b) = \frac{s}{\sqrt {{\sum_{i=1}^{n} (X_i - \overline X)^2} } }\)
Confidence interval of \(\; \beta\): \(\quad b \pm t_{n-2; α/2} \cdot SE(b)\)
Testing hypothesis:
\(\quad\) Null hypothesis: \(\quad H_0 : \beta = \beta_0\)
\(\quad\) Test statistic: \(\quad t = \frac{b - \beta_0 } { SE (b) }\)
\(\quad\) rejection region:
\(\qquad\) \(H_1 : \beta \lt \beta_0\): \(\; t < - t_{n-2; α}\)
\(\qquad\) \(H_1 : \beta \gt \beta_0\): \(\; t > t_{n-2; α}\)
\(\qquad\) \(H_1 : \beta \ne \beta_0\): \(\; |t| > t_{n-2; α/2}\)
The inference for the parameter \(\alpha\), which is the intercept of the regression line, can be summarized below. The parameter \(\alpha\) is not so interesting in most of the analysis because it represents the average value of the response variable when an independent variable is 0.
Point estimate: \(\quad \small a = \overline Y - b \overline X , \quad a \sim N( \alpha, ( \frac{1}{n} + \frac {{\overline X }^2} { \sum_{i=1}^{n} (X_i - \overline X )^2 } ) \cdot \sigma^2 ) \)
Standard error of estimate \(a\): \(\small \quad SE(a) = s \cdot \sqrt {\frac{1}{n} + \frac {{\overline X }^2} { \sum_{i=1}^{n} (X_i - \overline X )^2 } ) } \)
Confidence interval of \(\; \alpha\): \(\quad a \pm t_{n-2; α/2} \cdot SE(a)\)
Testing hypothesis:
\(\quad\) Null hypothesis: \(\quad H_0 : \alpha = \alpha_0\)
\(\quad\) Test statistic: \(\quad t = \frac{a - \alpha_0 } { SE (a) }\)
\(\quad\) rejection region:
\(\qquad\) \(H_1 : \alpha \lt \alpha_0\): \(\; t < - t_{n-2; α}\)
\(\qquad\) \(H_1 : \alpha \gt \alpha_0\): \(\; t > t_{n-2; α}\)
\(\qquad\) \(H_1 : \alpha \ne \alpha_0\): \(\; |t| > t_{n-2; α/2}\)
At any point in \(X = X_0\), the dependent variable \(Y\) has an average value \(\mu_{Y|x} = \alpha + \beta X_0\). Estimation of \(\mu_{Y|x}\) is also considered an important parameter because it means predicting the mean value of \(Y\) .
Point estimate: \(\quad {\hat Y}_0 = a + b X_0 \)
Standard error of estimate \({\hat Y}_0\): \(\small \quad SE({\hat Y}_0) = s \cdot \sqrt { \frac{1}{n} + \frac { (X_0 - \overline X )^2} { \sum_{i=1}^{n} (X_i - \overline X )^2 } } \)
Confidence interval of \(\; \mu_{Y|x}\): \(\quad {\hat Y}_0 \pm t_{n-2; α/2} \cdot SE ({\hat Y}_0 )\)
1) Predict the amount of sales when you have spent on advertising by 10.
2) Calculate the value of the residual standard error and the coefficient of determination.
3) Prepare an ANOVA table and test it using the 5% significance level.
Answer
1) In Example 5.5.1, the calculation required to obtain the intercept and slope has already been made. The intercept and slope using this are as follows.
\(
\quad b = \small \frac {\sum_{i=1}^{n} (X_i - \overline X ) (Y_i - \overline Y )} { \sum_{i=1}^{n} (X_i - \overline X )^2 } \\
= \frac {151.2}{60.4} = 2.503
\)
\(
\quad a = \small \overline Y - b \overline X = 49.7 - 2.503 \times 8.4 = 28.672
\)
Therefore, the fitted regression line is \(\small \hat Y_i = 28.672 + 2.503 X_i \). <Figure 5.5.3> shows the fitted regression line on the original data. The slope value, 2.5033, means that if advertising cost increases by one (i.e., one million), sales increase by about 2.5 million.
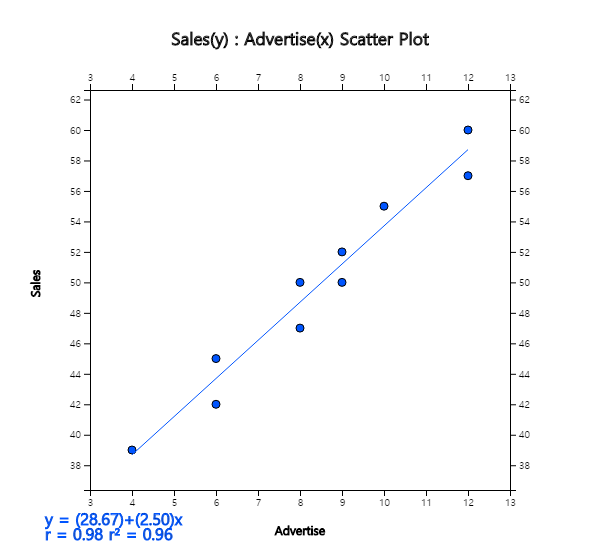
Prediction of the sales amount of a company with an advertising cost of 10 can be obtained using the fitted sample regression line as follows.
\(\quad \small 28.672 + (2.503)(10) = 53.702 \)
In other words, sales of 53.705 million are expected. That is not to say that all companies with advertising costs of 10 million USD have sales of 53.705 million USD, but that the average amount of their sales is about that. Therefore, there may be some differences in individual companies.
2) To obtain the residual standard error and the coefficient of determination, it is convenient to make the following Table 12.2.1. Here, the estimated value \(\small {\hat Y}_i\) of the sales from each value of \(\small {X}_i\) uses the fitted regression line.
\( \qquad \small {\hat Y}_i = 28.672 + 2.503 X_i \)
| Table 5.5.3 Useful calculations for the residual standard error and coefficient of determination | ||||||
|---|---|---|---|---|---|---|
| Number | \(\small X_i\) | \(\small Y_i\) | \(\small {\hat Y}_i\) | \(\small SST\) \(\small (Y_i - {\overline Y}_i )^2 \) |
\(\small SSR\) \(\small ({\hat Y}_i - {\overline Y}_i )^2 \) |
\(\small SSE\) \(\small (Y_i - {\hat Y}_i )^2 \) |
| 1 | 4 | 39 | 38.639 | 114.49 | 122.346 | 0.130 |
| 2 | 6 | 42 | 43.645 | 59.29 | 36.663 | 2.706 |
| 3 | 6 | 45 | 43.645 | 22.09 | 36.663 | 1.836 |
| 4 | 8 | 47 | 48.651 | 7.29 | 1.100 | 2.726 |
| 5 | 8 | 50 | 48.651 | 0.09 | 1.100 | 1.820 |
| 6 | 9 | 50 | 51.154 | 0.09 | 2.114 | 1.332 |
| 7 | 9 | 52 | 51.154 | 5.29 | 2.114 | 0.716 |
| 8 | 10 | 55 | 53.657 | 28.09 | 15.658 | 1.804 |
| 9 | 12 | 57 | 58.663 | 53.29 | 80.335 | 2.766 |
| 10 | 12 | 60 | 58.663 | 106.09 | 80.335 | 1.788 |
| Sum | 64 | 497 | 496.522 | 396.1 | 378.429 | 17.622 |
| Average | 8.4 | 49.7 | ||||
In Table 12.2.1, \(\small SST\) = 396.1, \(\small SSR\) = 378.429, \(\small SSE\) = 17.622. Here, the relationship of \(\small SST = SSE + SSR\) does not exactly match because number of digits calculation error. The sample variance of residuals is as follows.
\(\qquad \small s^2 = \frac{1}{n-2} \sum_{i=1}^{n} ( Y_i - {\hat Y}_i )^2 = \frac{17.622}{(10-2)} = 2.203 \)
Hence, the residual standard error is \(s\) = 1.484. The coefficient of determination is as follows.
\(\qquad \small R^2 = \frac{SSR}{SST} = \frac{378.429}{396.1} = 0.956\)
It means that 95.6% of the total variation in the observed 10 sales amounts can be explained by the simple linear regression model using a variable of advertising costs, so this regression line is quite useful.
3) The ANOVA table using the calculated sum of squares is as follows.
| Source | Sum of squares | Degrees of freedom | Mean Squares | \(\small F\) value |
|---|---|---|---|---|
| Regression | 378.42 | 1 | MSR = \(\frac{378.42}{1}\) = 378.42 | \(F_0 = \frac{378.42}{2.20} = 172.0\) |
| Error | 17.62 | 10-2 | MSE = \(\frac{17.62}{8} = 2.20\) | |
| Total | 396.04 | 10-1 |
Since the calculated \(\small F\) value of 172.0 is much greater than \(\small F_{1,8;\; 0.05} = 5.32 \), we reject the null hypothesis \(\small H_0 : \beta = 0\) with the significance level \(\alpha\) = 0.05. Inferences about each parameter with the result of a regression analysis are as follows.
\(\quad \small SE(b) = \frac{s}{\sqrt {{\sum_{i=1}^{n} (X_i - \overline X)^2} } } = \frac{1.484}{\sqrt 60.4} = 0.1908\)
Hence, the 95% confidence interval of \(\beta\) using \(t_{8;\; 0.025} \) = 2.056 is as follows.
\(\quad \small 2.5033 \pm (2.056)(0.1908)\)
\(\quad \small 2.5033 \pm 0.3922\)
\(\quad\) i.e. the interval (2.1110, 2.8956).
The test statistic for the hypothesis \(\small H_0 : \beta = 0\), is as follows.
\(\quad t= \frac{2.5033 - 0}{0.1908}\) = 13.12
Since \(t_{8; 0.025} \) = 2.056, the null hypothesis \(\small H_0 : \beta = 0\) is rejected with the significance level of \(\alpha\) = 0.05. This result of the two-sided test can be obtained from the confidence interval. Since the 95% confidence interval (1.7720, 3.2346) does not include 0, the null hypothesis \(\small H_0 : \beta = 0\) can be rejected.
\(\quad \small SE(a) = s \cdot \sqrt {\frac{1}{n} + \frac {{\overline X }^2} { \sum_{i=1}^{n} (X_i - \overline X )^2 } } = 1.484 \cdot \sqrt { \frac{1}{10} + \frac{8.4^2}{60.4} } \) = 1.670
Since the value of \(t\) statistic is \(\frac{29.672}{1.67}\) = 17.1657 and \(t_{8; 0.025}\) = 2.056, the null hypothesis \(\small H_0 : \alpha = 0\) is also rejected with the significance level \(\alpha\) = 0.05.
\(\small \quad SE({\hat Y}_0) = s \cdot \sqrt { \frac{1}{n} + \frac { (X_0 - \overline X )^2} { \sum_{i=1}^{n} (X_i - \overline X )^2 } } \)
\(\small \qquad \qquad \; = 1.484 \cdot \sqrt { \frac{1}{10} + \frac { (8 - 8.4)^2} {60.4 } }= 0.475 \)
Hence, the 95% confidence interval of \(\mu_{Y|x}\) is as follows.
\(\quad \small 48.696 \pm (2.056)×(0.475)\)
\(\quad \small 48.696 \pm 0.978\)
\(\quad\) i.e., the inteval is (47.718, 49.674).
We can calculate the confidence interval for other values of \(\small X\) similarly as follows.
\(\quad \) At \(\small \;X = 4, \quad 38.684 \pm (2.056)×(0.962) \Rightarrow (36.705, 40.663)\)
\(\quad \) At \(\small \;X = 6, \quad 47.690 \pm (2.056)×(0.656) \Rightarrow (42.341, 45.039)\)
\(\quad \) At \(\small \;X = 9, \quad 51.199 \pm (2.056)×(0.483) \Rightarrow (50.206, 52.192)\)
\(\quad \) At \(\small \;X =12, \quad 58.708 \pm (2.056)×(0.832) \Rightarrow (56.997, 60.419)\)
As we discussed, the confidence interval becomes wider as \(\small X\) is far from \(\small \overline X\).
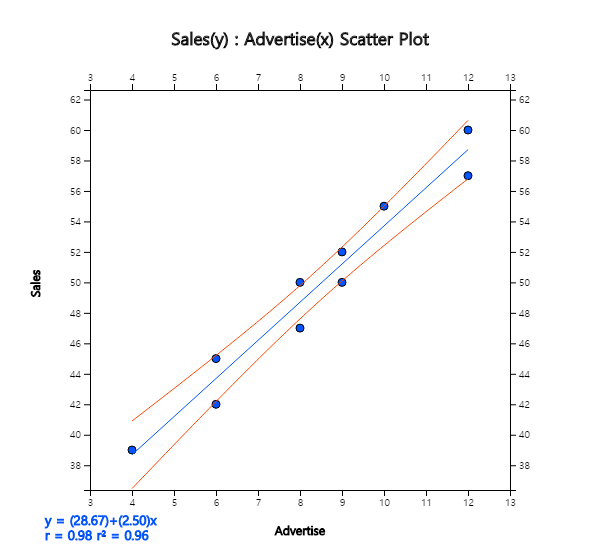
If you select the [Confidence Band] button from the options below, the regression graph of <Figure 5.5.3>, you can see the confidence band graph on the scatter plot together with the regression line as <Figure 5.5.4>. If you click the [Correlation and Regression] button, the inference result of each parameter will appear in the Log Area, as shown in <Figure 5.5.3>.

[]
5.5.3 Multiple linear regression
In the multiple linear regression model, it is assumed that the dependent variable \(Y\) and \(k\) number of independent variables have the following relational formulas: $$ Y_i = \beta_0 + \beta_1 X_{i1} + \cdots + \beta_k X_{ik} + \epsilon_i $$ It means that the dependent variable is represented by the linear function of the independent variables and a random variable that represents the error term as in the simple linear regression model. The assumption of the error terms is the same as the assumption in the simple linear regression. In the above equation, \(\beta_0\) is the intercept of \(Y\) axis and \(\beta_i\) is the slope of the Y axis and \(X_i\) which indicates the effect of \(X_i\) to \(Y\) when other independent variables are fixed.
| Table 5.5.4 Diameter, height and volume of tree | ||
|---|---|---|
| Diameter(\(cm\)) | Height(\(m\)) | Volume(\(m^3\)) |
| 21.0 | 21.33 | 0.291 |
| 21.8 | 19.81 | 0.291 |
| 22.3 | 19.20 | 0.288 |
| 26.6 | 21.94 | 0.464 |
| 27.1 | 24.68 | 0.532 |
| 27.4 | 25.29 | 0.557 |
| 27.9 | 20.11 | 0.441 |
| 27.9 | 22.86 | 0.515 |
| 29.7 | 21.03 | 0.603 |
| 32.7 | 22.55 | 0.628 |
| 32.7 | 25.90 | 0.956 |
| 33.7 | 26.21 | 0.775 |
| 34.7 | 21.64 | 0.727 |
| 35.0 | 19.50 | 0.704 |
| 40.6 | 21.94 | 1.084 |
Answer
Load the data saved at the following location of 『eStat』.
In the variable selection box, which appears by selecting the regression icon, select 'Y variable' by volume and select ‘by X variable’ as the diameter and height to display a scatter plot matrix, as shown in <Figure 5.5.6>. It can be observed that there is a high correlation between volume and diameter, and that volume and height, as well as diameter and height, are also somewhat related.
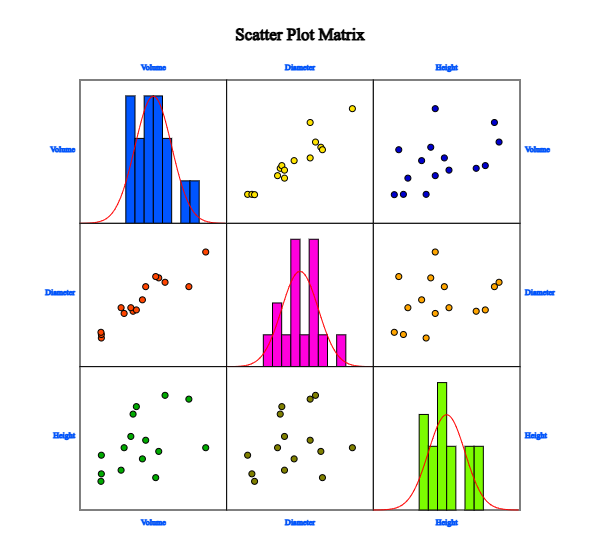
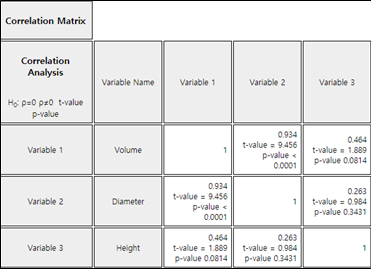
Since the volume is to be estimated using the diameter and height of the tree, the volume is the dependent variable \(\small Y\), and the diameter and height are independent variables \(\small X_1 , X_2\) respectively, and we can consider the following regression model.
\(\quad Y_i = \beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \epsilon_i , \quad i=1,2,...,15\)
The same analysis of multiple linear regression can be done using 『eStatU』 by following data input and clicking [Execute] button..
[]
| smoking rate \(x_1\) |
ratio of weight by height \(x_2\) |
time to continue to exercise \(y\) |
|---|---|---|
| 24 | 53 | 11 |
| 0 | 47 | 22 |
| 25 | 50 | 7 |
| 0 | 52 | 26 |
| 5 | 40 | 22 |
| 18 | 44 | 15 |
| 20 | 46 | 9 |
| 0 | 45 | 23 |
| 15 | 56 | 15 |
| 6 | 40 | 24 |
| 0 | 45 | 27 |
| 15 | 47 | 14 |
| 18 | 41 | 13 |
| 5 | 38 | 21 |
| 10 | 51 | 20 |
| 0 | 43 | 24 |
| 12 | 38 | 15 |
| 0 | 36 | 24 |
| 15 | 43 | 12 |
| 12 | 45 | 16 |
Here \(\mathbf {Y, X}, \boldsymbol{\beta , \epsilon}\) are defined as follows. $$ {\bf Y} = \left[ \matrix{ Y_1 \\ Y_2 \\ \cdot \\ \cdot \\ Y_n } \right], \quad {\bf X} = \left[ \matrix{ 1 & X_{11} & X_{12} & \cdots & X_{1k} \\ 1 & X_{21} & X_{22} & \cdots & X_{2k} \\ & & \cdots \\ & & \cdots \\ 1 & X_{n1} & X_{n2} & \cdots & X_{nk} } \right], \quad {\boldsymbol \beta} = \left[ \matrix{ \beta_0 \\ \beta_1 \\ \cdot \\ \cdot \\ \beta_k } \right], \quad {\boldsymbol \epsilon} = \left[ \matrix{ \epsilon_1 \\ \epsilon_2 \\ \cdot \\ \cdot \\ \epsilon_n } \right] $$
If the estimated regression coefficients are \({\bf b} = (b_0 , b_1 , ... , b_k )\), the estimate of the response variable \(Y\) is as follows. $$ {\hat Y}_i = b_0 + b_1 X_{i1} + \cdots + b_k X_{ik} $$ The residuals are as follows. $$ \begin{align} e_i &= Y_i - {\hat Y}_i \\ &= Y_i - (b_0 + b_1 X_{i1} + \cdots + b_k X_{ik} ) \end{align} $$ using a vector notation, the residual vector \(\bf e\) can be defined as follows. $$ \bf {e = Y - X b} $$ The standardized residual error and coefficient of determination are also used to investigate the validity of the estimated regression line in the multiple regression analysis. In the simple linear regression analysis, the computational formula for these measures was given as a function of the residuals, i.e., the observed value of \(Y\) and its predicted value have nothing to do with the number of independent variables. Therefore, the same formula can be used in the multiple linear regression, and there is only a difference in the value of the degrees of freedom that each sum of squares has. In the multiple linear regression analysis, the standard error of residuals is defined as follows. $$ s = \sqrt { \frac{1}{n-k-1} \sum_{i=1}^{n} (Y_i - {\hat Y}_i )^2} $$ As in simple linear regression, \(s^2\) is a statistic such as the residual mean squares (\(MSE\)).
The coefficient of determination is given in \(R^2 = \frac{SSR}{SST}\) and its interpretation is as shown in the simple linear regression. The same formula defines the sum of squares as in the simple linear regression, and it can be divided with corresponding degrees of freedom as follows. The table of the analysis of variance is shown in Table 5.5.5.
\(\quad\) Sum of squares \(\quad \quad \;\;SST = SSE + SSR\)
\(\quad\) Degrees of freedom \(\quad (n-1) = (n-k-1) + k\)
| Table 5.5.5 Analysis of variance table for multiple linear regression analysis | ||||
|---|---|---|---|---|
| Source | Sum of squares | Degrees of freedom | Mean Squares | F value |
| Regression | SSR | \(k\) | MSR = \(\frac{SSR}{k}\) | \(F_0 = \frac{MSR}{MSE}\) |
| Error | SSE | \(n-k-1\) | MSE = \(\frac{SSE}{n-k-1}\) | |
| Total | SST | \(n-1\) | ||
Point estimate: \(\quad b_i \)
Standard error of estimate \(b\): \(\quad SE(b_i) = \sqrt c_{ii} \cdot s \)
Confidence interval of \(\; \beta_i\): \(\quad b_i \pm t_{n-k-1; α/2} \cdot SE(b_i)\)
Testing hypothesis:
\(\quad\) Null hypothesis: \(\quad H_0 : \beta_i = \beta_{i0}\)
\(\quad\) Test statistic: \(\quad t = \frac{b_i - \beta_{i0} } { SE (b_i) }\)
\(\quad\) Rejection region:
\(\qquad\) \(\; H_1 : \beta_i \lt \beta_{i0}\): \(\; t < - t_{n-k-1;\; α}\)
\(\qquad\) \(\; H_1 : \beta_i \gt \beta_{i0}\): \(\; t > t_{n-k-1;\; α}\)
\(\qquad\) \(\; H_1 : \beta_i \ne \beta_{i0}\): \(\; |t| > t_{n-k-1;\; α/2}\)
Answer
In the options window below the scatter plot matrix in <Figure 5.5.6>, click [Regression Analysis] button. Then, you can find the estimated regression line, ANOVA table, as shown in <Figure 5.5.8> in the Log Area. The estimated regression equation is as follows.
\(\quad \small {\hat Y}_i = -1.024 + 0.037 X_1 + 0.024 X_2 \)
In the above equation, 0.037 represents the increase of the volume of the tree when the diameter (\(\small X_1\)) increases 1(cm).
The \(p\)-value calculated from the ANOVA table in <Figure 5.5.8> at \(\small F\) value of 73.12 is less than 0.0001, so you can reject the null hypothesis \(\small H_0 : \beta_1 = \beta_{2} = 0\) at the significance level \(\alpha\) = 0.05. The coefficient of determination, \(\small R^2\) = 0.924, implies that 92.4% of the total variances of the dependent variable are explained by the regression line. Based on the above two results, we can conclude that the diameter and height of the tree are quite useful in estimating the volume.

Since \(\small {SE}(b_1 ) = 0.003, \; {SE} (b_2 ) = 0.008 \) and \(t_{12; 0.025}\) = 2.179 from the result in <Figure 5.5.8>, the 95% confidence intervals for each regression coefficients can be calculated as follows. The difference between this result and the <Figure 5.5.8> due to the error in the calculation below the decimal point.
\(\quad \) 95% confidence interval for \(\beta_1 : \;\; \) 0.037 \(\pm\) (2.179)(0.003) \(\Rightarrow\) (0.029, ~0.045)
\(\quad \) 95% confidence interval for \(\beta_2 : \;\; \) 0.024 \(\pm\) (2.179)(0.008) \(\Rightarrow\) (0.006,~ 0.042)
In the hypothesis test of \(\small H_0 : \beta_i = 0 , \;\; H_1 : \beta_i \ne 0\) , each \(p\)-value is less than the significance level of 0.05, so you can reject each null hypothesis.
5.6 R and Python practice
R practice
[Colab]
| Normal Distribution | |
|---|---|
| pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE) | |
| q | quantile |
| mean | mean of normal distribution, default = 0. |
| sd | standard deviation of normal distribution, default = 1. |
| lower.tail | logical; if TRUE (default), probabilities are P[X≤x], otherwise P[X>x]. |
| log.p | logical; if TRUE, probabilities p are given as log(p). |
| Student t Distribution | |
|---|---|
| pt(q, df, ncp, lower.tail = TRUE, log.p = FALSE) | |
| q | quantile |
| df | degree of freedom(>0, maybe non-integer). df = Inf is allowed. |
| ncp | non-centrality parameter δ; currently except for rt(), accurate only for abs(ncp) <= 37.62. If omitted, use the central t distribution. |
| lower.tail | logical; if TRUE (default), probabilities are P[X≤x], otherwise P[X>x]. |
| log.p | logical; if TRUE, probabilities p are given as log(p). |
| F Distribution | |
|---|---|
| pf(q, df1, df2, ncp, lower.tail = TRUE, log.p = FALSE) | |
| q | quantile |
| df1, df2 | degree of freedom. Inf is allowed. |
| ncp | non-centrality parameter. If omitted, the central F distribution. |
| lower.tail | logical; if TRUE (default), probabilities are P[X≤x], otherwise P[X>x]. |
| log.p | logical; if TRUE, probabilities p are given as log(p). |
| # Example 5.2.1 Testing hypothesis for a population mean with known population standard deviation. # Enter mu_0, n, xbar, and population standard deviation, then calculate test statistic and p-value. |
|
mu0 <- 1500 n <- 30 xbar <- 1555 sigma <- 200 teststat <- (xbar - mu0) / (sigma / sqrt(n)) teststat [1] 1.506237 pvalue <- pnorm(teststat,0,1,lower.tail = FALSE) pvalue [1] 0.06600317 |
| # Since p-value is greater than the significance level 5%, we cannot reject the null hypothesis. |
| # Example 5.2.2 Testing hypothesis for a population mean with unknown population standard deviation. # Enter mu_0, n, xbar, and sample standard deviation, then calculate test statistic and p-value. |
|
mu0 <- 250 n <- 16 xbar <- 253 s <- 10 teststat <- (xbar - mu0) / (s / sqrt(n)) teststat [1] 1.2 pvalue <- pt(teststat, n-1, lower.tail = FALSE) pvalue [1] 0.1243749 |
| # Since p-value is greater than the significance level 5%, we cannot reject the null hypothesis. |
| # Example 5.3.1 Testing hypothesis for two populations means when population variances are equal. # Enter n1, n2, xbar1, xbar2, s1, and s2, then calculate the pooled variance, test statistic and p-value. |
|
n1 <- 15 n2 <- 14 xbar1 <- 275 xbar2 <- 269 s1 <- 12 s2 <- 10 pooledvar <- ((n1-1)*s1^2 + (n2-1)*s2^2) / (n1+n2-2) pooledvar [1] 122.8148 teststat <- (xbar1 - xbar2) / sqrt(pooledvar/n1 + pooledvar/n2) teststat [1] 1.456923 pvalue <- 2 * pt(teststat, n1+n2-2, lower.tail = FALSE) pvalue [1] 0.1566703 |
| # Since p-value is greater than the significance level 5%, we cannot reject the null hypothesis. |
| Fit an Analysis of Variance Model using aov() | |
|---|---|
| aov(formula, data = NULL, projections = FALSE, qr = TRUE, contrasts = NULL, ...) | |
| formula | A formula specifying the model. |
| data | A data frame in which the variables specified in the formula will be found. If missing, the variables are searched for in the standard way. |
| projections | Logical flag: should the projections be returned? |
| qr | Logical flag: should the QR decomposition be returned? |
| contrasts | A list of contrasts to be used for some of the factors in the formula. These are not used for any Error term, and supplying contrasts for factors only in the Error term will give a warning. |
| # Example 5.4.1 Testing hypothesis for several populations means; one-way ANOVA. # Enter data and change the level as a factor (as.factor()). |
|
y <- c(81,75,69,90,72,83, 65,80,73,79,81,69, 72,67,62,76,80, 89,94,79,88) f <- c(rep(1,6), rep(2,6), rep(3,5), rep(4,4)) af <- as.factor(f) ymean <- tapply(y, af, mean); ymean
1 2 3 4
78.33333 74.50000 71.40000 87.50000
boxplot(y ~ af) 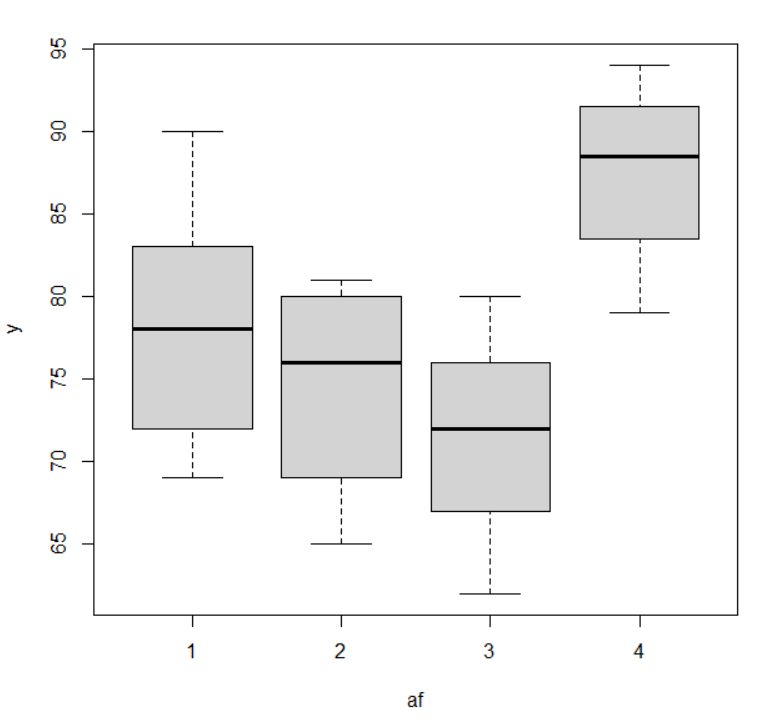
<Figure 5.6.1> Box plot for each grade
an1 <- aov(y ~ af) summary(an1)
Call:
aov(formula = y ~ af)
Terms:
af Residuals
Sum of Squares 643.6333 839.0333
Deg. of Freedom 3 17
Residual standard error: 7.025304
Estimated effects may be unbalanced
> summary(an1)
Df Sum Sq Mean Sq F value Pr(>F)
af 3 643.6 214.54 4.347 0.0191 *
Residuals 17 839.0 49.35
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
|
| # Since p-value (Pr(>F) = 0.0191 is less than the significance level 5%, we reject the null hypothesis. |
| Fitting Linear Models using lm() lm is used to fit linear models, including multivariate ones. |
|
|---|---|
| lm(formula, data, subset, weights, na.action, method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE, singular.ok = TRUE, contrasts = NULL, offset, ...) | |
| formula | an object of class "formula": a symbolic description of the model to be fitted. |
| data | an optional data frame, list or environment containing the variables in the model. |
| subset | an optional vector specifying a subset of observations to be used in the fitting process. |
| weights | an optional vector of weights to be used in the fitting process. Should be NULL or a numeric vector. If non-NULL, weighted least squares is used with weights weights (that is, minimizing sum(w*e^2)); otherwise ordinary least squares is used. |
| na.action | a function which indicates what should happen when the data contain NAs. The default is set by the na.action setting of options, and is na.fail if that is unset. The ‘factory-fresh’ default is na.omit. Another possible value is NULL, no action. Value na.exclude can be useful. |
| method | the method to be used; for fitting, currently only method = "qr" is supported; method = "model.frame" returns the model frame (the same as with model = TRUE, see below). |
| model, x, y, qr | logicals. If TRUE the corresponding components of the fit (the model frame, the model matrix, the response, the QR decomposition) are returned. |
| singular.ok | logical. If FALSE (the default in S but not in R) a singular fit is an error. |
| contrasts | an optional list. See the contrasts.arg of model.matrix.default. |
| offsets | this can be used to specify an a priori known component to be included in the linear predictor during fitting. This should be NULL or a numeric vector or matrix of extents matching those of the response. One or more offset terms can be included in the formula instead or as well, and if more than one are specified their sum is used. See model.offset. |
| # Example 5.5.1 Regression analysis. # Enter data and change the level as a factor (as.factor()). |
|
x <- c(4,6,6,8,8,9,9,10,12,12) y <- c(39,42,45,47,50,50,52,55,57,60) rg <- lm(y ~ x); rg
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
28.672 2.503
plot(x, y); abline(rg) 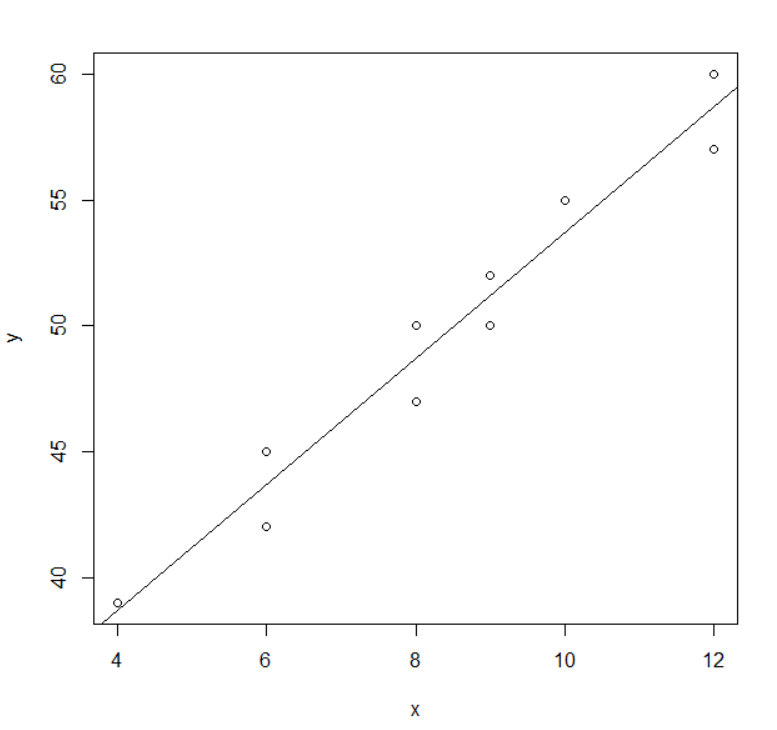
<Figure 5.6.2> Simple linear regression
summary(rg)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-1.7119 -1.5695 0.5563 1.2931 1.3079
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 28.6722 1.6703 17.17 1.35e-07 ***
x 2.5033 0.1908 13.12 1.09e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.483 on 8 degrees of freedom
Multiple R-squared: 0.9556, Adjusted R-squared: 0.95
F-statistic: 172.1 on 1 and 8 DF, p-value: 1.085e-06
|
| # Example 5.5.3 Multiple regression analysis. # Enter data and change the level as a factor (as.factor()). |
|
y <- c(0.291,0.291,0.288,0.464,0.532,0.557,0.441,0.515,0.603,0.628,0.956,0.775,0.727,0.704,1.084) x1 <- c(21.0,21.8,22.3,26.6,27.1,27.4,27.9,27.9,29.7,32.7,32.7,33.7,34.7,35.0,40.6) x2 <- c(21.33,19.81,19.20,21.94,24.68,25.29,20.11,22.86,21.03,22.55,25.90,26.21,21.64,19.50,21.94) rg2 <- lm(y ~ x1+x2); rg2 Call: lm(formula = y ~ x1 + x2) Coefficients: (Intercept) x1 x2 -1.02357 0.03697 0.02366summary(rg2)
Call:
lm(formula = y ~ x1 + x2)
Residuals:
Min 1Q Median 3Q Max
-0.09087 -0.03822 -0.02772 0.03320 0.15786
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.023572 0.187535 -5.458 0.000146 ***
x1 0.036968 0.003491 10.590 1.92e-07 ***
x2 0.023663 0.008321 2.844 0.014792 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.06947 on 12 degrees of freedom
Multiple R-squared: 0.9242, Adjusted R-squared: 0.9115
F-statistic: 73.12 on 2 and 12 DF, p-value: 1.902e-07
|
Python practice
[Colab]
|
# Example 5.2.1 Testing hypothesis for a population mean with known population standard deviation. # # Enter mu_0, n, xbar, and population standard deviation, then calculate test statistic and p-value. import math from scipy.stats import norm mu0 = 1500 n = 30 xbar = 1555 sigma = 200 teststat = (xbar - mu0) / (sigma / math.sqrt(n)) print(f"Test statistic: {teststat}") pvalue = norm.sf(teststat) # Survival function (1 - CDF) print(f"P-value: {pvalue}") Test statistic: 1.5062370331392068 P-value: 0.06600316790918383 |
|
# Example 5.2.2 Testing hypothesis for a population mean with unknown population standard deviation. # Enter mu_0, n, xbar, and sample standard deviation, then calculate test statistic and p-value. import math from scipy.stats import # Example 5.2.2 Testing hypothesis for a population mean with unknown population standard deviation. # Enter mu_0, n, xbar, and sample standard deviation, then calculate test statistic and p-value. mu0 = 250 n = 16 xbar = 253 s = 10 teststat = (xbar - mu0) / (s / math.sqrt(n)) print(f"Test statistic: {teststat}") pvalue = t.sf(teststat, n-1) # Survival function (1 - CDF) print(f"P-value: {pvalue}") Test statistic: 1.2 P-value: 0.12437489369401128 |
|
# prompt: # Example 5.3.1 Testing hypothesis for two populations means when population variances are equal. # # Enter n1, n2, xbar1, xbar2, s1, and s2, then calculate the pooled variance, test statistic and p-value. import math from scipy.stats import norm from scipy.stats import t # Example 5.3.1 Testing hypothesis for two populations means when population variances are equal. # Enter n1, n2, xbar1, xbar2, s1, and s2, then calculate the pooled variance, test statistic and p-value. n1 = 15 n2 = 14 xbar1 = 275 xbar2 = 269 s1 = 12 s2 = 10 pooledvar = ((n1 - 1) * s1**2 + (n2 - 1) * s2**2) / (n1 + n2 - 2) print(f"Pooled Variance: {pooledvar}") teststat = (xbar1 - xbar2) / math.sqrt(pooledvar / n1 + pooledvar / n2) print(f"Test statistic: {teststat}") pvalue = 2 * t.sf(abs(teststat), n1 + n2 - 2) # Use abs for two-tailed test, sf for survival function print(f"P-value: {pvalue}") Pooled Variance: 122.81481481481481 Test statistic: 1.4569227333394668 P-value: 0.15667027233049496 |
|
# prompt: # Example 5.4.1 Testing hypothesis for several populations means; one-way ANOVA. # # Enter data and change the level as a factor (as.factor()). # y <- c(81,75,69,90,72,83, 65,80,73,79,81,69, 72,67,62,76,80, 89,94,79,88) # f <- c(rep(1,6), rep(2,6), rep(3,5), rep(4,4)) # af <- as.factor(f) # ymean <- tapply(y, af, mean) # ymean import statsmodels.formula.api as sm # Import the correct module for anova_lm from statsmodels.stats.anova import anova_lm # Example 5.4.1 Testing hypothesis for several populations means; one-way ANOVA. y = [81,75,69,90,72,83, 65,80,73,79,81,69, 72,67,62,76,80, 89,94,79,88] f = [1,1,1,1,1,1, 2,2,2,2,2,2, 3,3,3,3,3, 4,4,4,4] # Create a pandas DataFrame import pandas as pd df = pd.DataFrame({'y': y, 'f': f}) # Fit the one-way ANOVA model model = sm.ols('y ~ C(f)', data=df).fit() # Print the ANOVA table # Call anova_lm directly from the imported module print(anova_lm(model, typ=2))
sum_sq df F PR(>F)
C(f) 643.633333 3.0 4.346973 0.019054
Residual 839.033333 17.0 NaN NaN
# Create the boxplot plt.figure(figsize=(8, 6)) # Adjust figure size if needed df.boxplot(column='y', by='af') plt.title('Boxplot of y by af') plt.suptitle('') # Remove default suptitle plt.xlabel('af') plt.ylabel('y') plt.show() 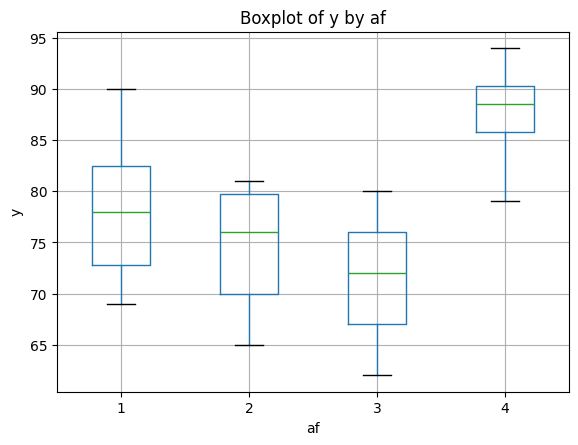
import statsmodels.formula.api as sm sum_sq df F PR(>F) C(af) 643.633333 3.0 4.346973 0.019054 Residual 839.033333 17.0 NaN NaN import math from scipy.stats import norm from scipy.stats import t import statsmodels.formula.api as sm from statsmodels.stats.anova import anova_lm import pandas as pd import matplotlib.pyplot as plt |
|
# Example 5.5.1 Regression analysis. # Enter data and change the level as a factor (as.factor()). x = [4,6,6,8,8,9,9,10,12,12] y = [39,42,45,47,50,50,52,55,57,60] # Create a pandas DataFrame df = pd.DataFrame({'x': x, 'y': y}) # Fit the linear regression model rg = sm.ols('y ~ x', data=df).fit() # Print the regression summary print(rg.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.956
Model: OLS Adj. R-squared: 0.950
Method: Least Squares F-statistic: 172.1
Date: Sat, 19 Apr 2025 Prob (F-statistic): 1.09e-06
Time: 13:32:00 Log-Likelihood: -17.016
No. Observations: 10 AIC: 38.03
Df Residuals: 8 BIC: 38.64
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 28.6722 1.670 17.166 0.000 24.820 32.524
x 2.5033 0.191 13.117 0.000 2.063 2.943
==============================================================================
Omnibus: 6.181 Durbin-Watson: 3.388
Prob(Omnibus): 0.045 Jarque-Bera (JB): 1.423
Skew: -0.309 Prob(JB): 0.491
Kurtosis: 1.258 Cond. No. 31.5
==============================================================================
# Plot the data and regression line plt.figure(figsize=(8, 6)) plt.scatter(x, y) plt.plot(x, rg.predict(), color='red') plt.xlabel('x') plt.ylabel('y') plt.title('Regression Analysis') plt.show() 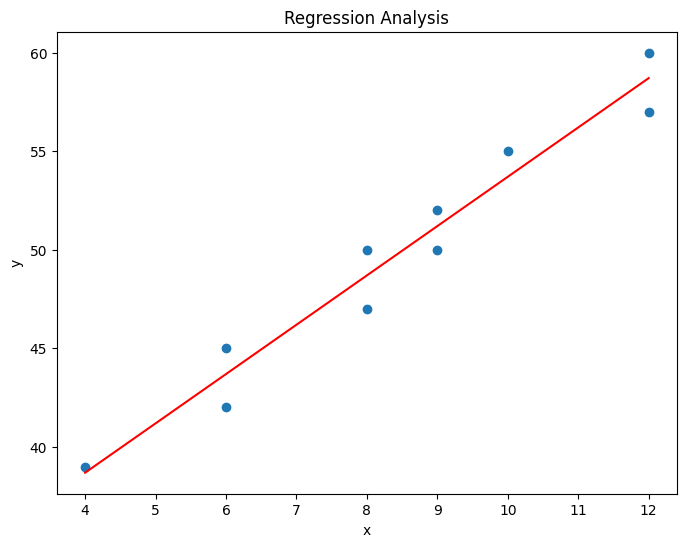
|
|
# Example 5.5.3 Multiple regression analysis. # Enter data and change the level as a factor (as.factor()). import pandas as pd import statsmodels.formula.api as sm y = [0.291,0.291,0.288,0.464,0.532,0.557,0.441,0.515,0.603,0.628,0.956,0.775,0.727,0.704,1.084] x1 = [21.0,21.8,22.3,26.6,27.1,27.4,27.9,27.9,29.7,32.7,32.7,33.7,34.7,35.0,40.6] x2 = [21.33,19.81,19.20,21.94,24.68,25.29,20.11,22.86,21.03,22.55,25.90,26.21,21.64,19.50,21.94] # Create a pandas DataFrame df = pd.DataFrame({'y': y, 'x1': x1, 'x2': x2}) # Fit the multiple linear regression model rg2 = sm.ols('y ~ x1 + x2', data=df).fit() # Print the regression summary print(rg2.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.924
Model: OLS Adj. R-squared: 0.912
Method: Least Squares F-statistic: 73.12
Date: Sat, 19 Apr 2025 Prob (F-statistic): 1.90e-07
Time: 13:32:28 Log-Likelihood: 20.392
No. Observations: 15 AIC: -34.78
Df Residuals: 12 BIC: -32.66
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -1.0236 0.188 -5.458 0.000 -1.432 -0.615
x1 0.0370 0.003 10.590 0.000 0.029 0.045
x2 0.0237 0.008 2.844 0.015 0.006 0.042
==============================================================================
Omnibus: 4.763 Durbin-Watson: 2.566
Prob(Omnibus): 0.092 Jarque-Bera (JB): 2.434
Skew: 0.953 Prob(JB): 0.296
Kurtosis: 3.511 Cond. No. 389.
==============================================================================
|
5.7 Exercise
5.1 A psychologist is working on physically disabled workers. Based on experience, the psychologist believed that the average social (relationship) score of these disabled workers was greater than 80. Twenty employees were sampled from the score population to obtain the following result:
99, 69, 91, 97, 70, 99, 72, 74, 74, 76, 96, 97, 68, 71, 99, 78, 76, 78, 83, 66
The psychologist wants to know if the average social score of the population is correct. Assume that the population follows a normal distribution and its standard deviation is 10. Test with a significance level of 0.05.
5.2 The following is the weights of the 10 employees randomly selected who are working in the shipping department of a wholesale food company.
154, 154, 186, 243, 159, 174, 183, 163, 192, 181 (unit pound)
Based on this data, can you say that the average weight of employees working in the shipping department is greater than 160 pound? Use the significance level of 5%.
5.3 In a large manufacturer, the company manager claims that the average adaptation score of all unskilled workers is greater than 60. Forty unskilled workers were selected randomly to check this claim, and their test scores of adaptation scores were as follows.
73 57 96 78 74 42 55 44 91 91 50 65 46 63 82 60 97 79 85 79
92 50 42 46 86 81 81 83 64 76 40 57 78 66 84 96 94 70 70 81
Test the hypothesis at the significance level of 0.05 whether the manager's argument is correct. What is the \(p\)-value?
5.4 An analyst studies two types of advertising methods (A and B) retailers tried. The variable is the sum spent on advertising over the past year. The following are the sample statistics extracted independently from retailers of each type. (Unit million USD)
Type A: \(\small n_1 = 60, \; {\overline x}_1 = 14.8, \; s_1^2 = 0.180\)
Type B: \(\small n_1 = 70, \; {\overline x}_2 = 14.5, \; s_2^2 = 0.133\)
From these data, can you conclude that type A retailers have invested more in advertising than type B retailers? (Significance level = 0.05)
5.5 Below are the entrance exam results for selecting new employees at a particular company. Test whether the male population mean is equal to the female population mean using the significance level 5%.
| Male | Female |
|---|---|
| 49 86 40 45 48 93 97 58 58 98 58 82 52 56 50 85 80 60 62 80 62 72 65 60 64 70 78 67 69 88 |
60 72 66 65 75 78 62 64 74 58 68 72 67 61 62 72 79 71 74 73 |
5.6 An industrial psychologist thinks that the significant factor that workers change jobs is self-esteem to workers' work. The scholar believes that workers who change jobs frequently (group A) have lower self-esteem than those who do not (group B). The score data on self-esteem were collected independently by sampling from each group.
Group A: 60 45 42 62 68 54 52 55 44 41
Group B: 70 72 74 74 76 91 71 78 78 83 50 52 66 65 53 52
Can this data support the psychologist's idea? Assume that the population scores are normally distributed and that the population variance is unknown but the same. (Significance level = 0.01)
5.7 A company used four exhibition methods to test customers' responses to new products (A, B, C, and D). Each exhibition method was used in nine stores by selecting 36 stores that met the company's criteria. The total sales in USD for the weekend are shown in the following table.
| Method A | Method B | Method C | Method D |
|---|---|---|---|
| 5 | 2 | 2 | 6 |
| 6 | 2 | 2 | 6 |
| 7 | 2 | 3 | 7 |
| 7 | 3 | 3 | 8 |
| 8 | 3 | 2 | 8 |
| 6 | 2 | 2 | 8 |
| 7 | 3 | 2 | 6 |
| 7 | 3 | 3 | 6 |
| 6 | 2 | 3 | 6 |
5.8 The following table shows mileages in km per liter of gasoline obtained from experiments to compare three brands of gasoline. In this experiment, seven cars of the same type were used in a similar situation to reduce the variation of the car.
| Gasoline A | Gasoline B | Gasoline C |
|---|---|---|
| 14 | 20 | 20 |
| 19 | 21 | 26 |
| 19 | 18 | 23 |
| 16 | 20 | 24 |
| 15 | 19 | 23 |
| 17 | 19 | 25 |
| 20 | 18 | 23 |
5.9 The result of a survey on job satisfaction of three companies (A, B, and C) is as follows: Test whether the averages of job satisfaction of the three companies are different with a 5% significance level.
| Company A | Company B | Company C |
|---|---|---|
| 69 | 56 | 71 |
| 67 | 63 | 72 |
| 65 | 55 | 70 |
| 59 | 59 | 68 |
| 68 | 52 | 74 |
| 61 | 57 | |
| 66 |
5.10 The following data shows studying time for a week (\(\small X\)) and the grade (\(\small Y\)) of six students.
| Studying time (\(\small X\)) | Grade (\(\small Y\)) |
|---|---|
| 15 | 2.0 |
| 28 | 2.7 |
| 13 | 1.3 |
| 20 | 1.9 |
| 4 | 0.9 |
| 10 | 1.7 |
5.11 An economist argues that there is a clear relationship between coffee and sugar prices. 'When people buy coffee, they will also buy sugar. Isn't it natural that the higher the demand, the higher the price?' We collected the following sample data to test his theory.
| Year | Coffee price | Sugar Price |
|---|---|---|
| 1985 | 0.68 | 0.245 |
| 1986 | 1.21 | 0.126 |
| 1987 | 1.92 | 0.092 |
| 1988 | 1.81 | 0.086 |
| 1989 | 1.55 | 0.101 |
| 1990 | 1.87 | 0.223 |
| 1991 | 1.56 | 0.212 |
5.12 A health scientist randomly selected 20 people to determine the effects of smoking and obesity on their physical strength and examined the average daily smoking rate (\(x_1\), number/day), the ratio of weight by height (\(x_2\), kg/m), and the time to continue to exercise with a certain intensity (\(y\), in hours). Test whether smoking and obesity can affect your exercising time with a certain intensity. Apply a multiple regression model by using 『eStat』.
| smoking rate \(x_1\) |
ratio of weight by height \(x_2\) |
Atime to continue to exercise \(y\) |
|---|---|---|
| 24 | 53 | 11 |
| 0 | 47 | 22 |
| 25 | 50 | 7 |
| 0 | 52 | 26 |
| 5 | 40 | 22 |
| 18 | 44 | 15 |
| 20 | 46 | 9 |
| 0 | 45 | 23 |
| 15 | 56 | 15 |
| 6 | 40 | 24 |
| 0 | 45 | 27 |
| 15 | 47 | 14 |
| 18 | 41 | 13 |
| 5 | 38 | 21 |
| 10 | 51 | 20 |
| 0 | 43 | 24 |
| 12 | 38 | 15 |
| 0 | 36 | 24 |
| 15 | 43 | 12 |
| 12 | 45 | 16 |