Chapter 8. Unsupervised Learning: Clustering Analysis
[presentation] [book]
- 8.1 Basic concepts of unsupervised learning and clustering
- 8.2 Hierarchical clustering model
- 8.2.1 Method of linkage
- 8.2.2 R and Python practice - Hierarchical clustering
- 8.3 \(\small K\)-means clustering model
- 8.3.1 R and Python practice - \(\small K\)-Means clustering
- 8.4 Exercise
CHAPTER OBJECTIVES
8.1 Basic concepts of clustering analysis
Clustering analysis is a method of forming clusters based on the similarity or relationship between each data, such that the data in a cluster are similar and the data in other clusters are different. At this time, the higher the similarity within a cluster, the better, and the differences between clusters should be as different as possible. However, it is generally difficult to define a cluster, and it is unclear how many clusters to divide into. Many types of clustering analysis models have been developed to apply to various types of data, but there is hardly a single clustering analysis model that is satisfactory for all types of applications. Each clustering analysis model can show different performance when the data dimension is low or high, when the data size is small or large, when the data density is small or high when there are few or many outliers or extreme points, and when the data properties are discrete or continuous. In general, after applying several clustering analysis models, an appropriate model is selected based on the analyst's judgment.
In this chapter, we first introduce the hierarchical clustering model, which has been used for a long time. Then, we introduce the \(\small K\)-means clustering, which is widely used.
Classification of clustering analysis models
Clustering analysis models can also be divided into exclusive clustering analysis, where one data must belong to one cluster, and inclusive clustering analysis, where one data can belong to multiple clusters. The \(\small K\)-means clustering model is an exclusive clustering analysis, and the fuzzy clustering model and the mixed distribution clustering model are inclusive clustering analyses. The fuzzy cluster and mixed distribution clustering models indicate the weight or probability that each data belongs to each cluster as a number between 0 and 1. However, since the inclusive clustering analysis model generally classifies one data into a group with a higher probability, the final data cluster can be an exclusive clustering analysis.
In addition, clustering analysis models are also classified into prototype-based models, density-based models, and graph-based models. The prototype-based model determines the form of the cluster based on how close the data is to the prototype of each cluster, which has been determined in advance. The \(\small K\)-means clustering model is a prototype-based model. In the case of continuous data, the cluster average is usually set as the prototype, and in the case of discrete data, the mode of the cluster is used as the prototype. The density-based model is a method that considers an area where data is distributed as a cluster when the density is very high. The graph-based model is a method that considers each data as a node, connects the nodes based on a set distance, and then determines the data corresponding to the connected nodes as a cluster. The Kohonen clustering model belongs to this.
Evaluation of clustering analysis models
Various measures can be considered for evaluating these factors, such as the response within a cluster, cohesion and separation between clusters. In the case of clustering models that utilize distance or similarity between data, the cohesion of cluster \(\small G_{i}\) and the separation between two clusters \(\small G_{i}\) and \(\small G_{j}\) are defined as follows. Here, \(\small d(\boldsymbol x, \boldsymbol y)\) is the distance between data \(\boldsymbol x\) and data \(\boldsymbol y\). $$ \small \begin{align} \text{Cohesion} (G_{i}) &= \sum_{\boldsymbol x , \; \boldsymbol y \; \in \; G_{i}} \; d(\boldsymbol x, \boldsymbol y) \\ \text{Separation} (G_{i} , G_{j}) &= \sum_{\boldsymbol x \; \in \; G_{i}} \; \sum_{\boldsymbol x \; \in \; G_{j}} \; d(\boldsymbol x, \boldsymbol y) \end{align} $$
In the clustering model based on the prototype, the cohesion and separation are defined as follows when the centroids of clusters \(\small G_{i}\) and clusters \(\small G_{j}\) are \(\small \boldsymbol c_{i}\) and \(\small \boldsymbol c_{j}\), respectively. $$ \small \begin{align} \text{Cohesion} (G_{i}) &= \sum_{\boldsymbol x \; \in \; G_{i}} \; d(\boldsymbol x, \boldsymbol c_{i} ) \\ \text{Separation} (G_{i} , G_{j}) &= d(\boldsymbol c_{i}, \boldsymbol c_{j}) \end{align} $$ In the case of cohesion, if the distance \(d(\boldsymbol x, \boldsymbol c_{i} )\) between the data \(\boldsymbol x \) of cluster and the center \(\boldsymbol c_{i} \) is defined as the squared Euclidean distance, the cohesion of cluster \(\small G_{i}\) becomes the sum of squared error (SSE).
When there are \(\small K\) clusters and the number of data in cluster \(\small G_{i}\) is \(\small n_{i}\), the cohesion of the entire clustering model is calculated as the weighted sum of the cohesion of each cluster, and the weight value \(\small w_{i}\) can be \(\small n_{i}\), \(\small \frac{1}{n_{i}}\), or other various measures depending on the situation. $$ \small \text{Cohesion of total model} = \sum_{i=1}^{K} \; w_{i} \times (\text{Cohesion of cluster} \; G_{i} ) $$
8.2 Hierachical clustering model
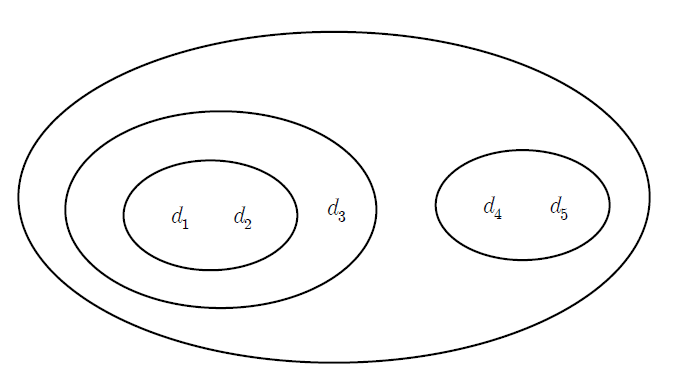
The result of hierarchical clustering is often displayed in a dendrogram similar to a tree, as shown on <Figure 8.2.1>, which shows the relationship between clusters and subclusters and the order in which clusters are formed. The subset plot displays the entire data as one set, as shown in <Figure 8.2.2>, and displays each hierarchical cluster as a subset plot within this set.

| Step 1 | Consider each data as one cluster and calculate the similarity matrix of all data. |
| Step 2 | repeat |
| Step 3 | \(\qquad\)Group the two closest clusters into one cluster. |
| Step 4 | \(\qquad\)Obtain the similarity matrix between all clusters including the newly formed cluster. |
| Step 5 | until (the number of clusters becomes one) |
8.2.1 Method of linkage
A. Single linkage
| Table 8.2.1 Five observed data and the matrix of squared Euclid distances | ||||||
|---|---|---|---|---|---|---|
| Distance/th> | ||||||
| Data | \(\small (x_{1}, \small x_{2})\) | \(\small A\) | \(\small B\) | \(\small C\) | \(\small D\) | \(\small E\) |
| \(\small A\) | (1, 5) | 0 | ||||
| \(\small B\) | (2, 4) | 2 | 0 | |||
| \(\small C\) | (4, 6) | 10 | 8 | 0 | ||
| \(\small D\) | (4, 3) | 13 | 5 | 9 | 0 | |
| \(\small E\) | (5, 3) | 20 | 10 | 10 | 1 | 0 |
Answer
Since the distance between data \(\small D\) and \(\small E\) is 1, which is the minimum, \(\small (DE)\) is the first cluster, and the distance between cluster \(\small (DE)\) and the remaining data is calculated using the single linkage method, and the distance matrix is modified as follows.
\( \small \qquad d((DE), A) = min(d(D,A), d(E,A)) = min(13, 20) = 13 \)
\( \small \qquad d((DE), B) = min(d(D,B), d(E,B)) = min(5, 10) = 5 \)
\( \small \qquad d((DE), C) = min(d(D,C), d(E,C)) = min(9, 10) = 9 \)
| Table 8.2.2 Modified distance matrix with cluster \(\small (DE)\) using the single linkage | ||||
|---|---|---|---|---|
| Distance/th> | ||||
| Cluster | \(\small A\) | \(\small B\) | \(\small C\) | \(\small (DE)\) |
| \(\small A\) | 0 | |||
| \(\small B\) | 2 | 0 | ||
| \(\small C\) | 10 | 8 | 0 | |
| \(\small (DE)\) | 13 | 5 | 9 | 0 |
Here, the minimum distance is \(\small d(A,B)\) = 2, so \(\small (AB)\) becomes the next cluster. If we calculate the distance between clusters \(\small (AB)\) and \(\small C\) , \(\small (DE)\) using the single linkage method and modify the distance matrix, we get the following.
\( \small \qquad d((AB), C) = min(d(A,C), d(B,C)) = min(10, 8) = 8 \)
\( \small \qquad d((AB), (DE)) = min(d(A, (DE)), d(B,(DE)) = min(13, 5) = 5 \)
| Table 8.2.3 Modified distance matrix with cluster \(\small (AB)\) using the single linkage | ||||
|---|---|---|---|---|
| Distance/th> | ||||
| Cluster | \(\small (AB)\) | \(\small C\) | \(\small (DE)\) | |
| \(\small (AB)\) | 0 | |||
| \(\small C\) | 8 | 0 | ||
| \(\small (DE)\) | 5 | 9 | 0 | |
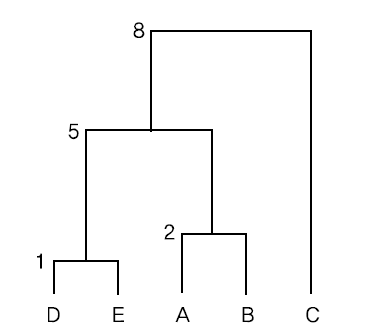
Here, the minimum distance is \(\small (d(AB), (DE))\) = 5, so \(\small (AB)(DE)\) becomes the next cluster. If we calculate the distance between clusters \(\small (AB)(DE)\) and \(\small C\) using the single linkage method, we get the following.
\( \small \qquad d((AB)(DE), C) = min(d((AB), C), d((DE), C)) = min(8, 9) = 8 \)
If the above single linkage method is displayed as a dendrogram, it is as shown in <Figure 8.2.3>.
B. Complete linkage
| Table 8.2.4 Five observed data and the matrix of squared Euclid distances | ||||||
|---|---|---|---|---|---|---|
| Distance/th> | ||||||
| Data | \(\small (x_{1}, \small x_{2})\) | \(\small A\) | \(\small B\) | \(\small C\) | \(\small D\) | \(\small E\) |
| \(\small A\) | (1, 5) | 0 | ||||
| \(\small B\) | (2, 4) | 2 | 0 | |||
| \(\small C\) | (4, 6) | 10 | 8 | 0 | ||
| \(\small D\) | (4, 3) | 13 | 5 | 9 | 0 | |
| \(\small E\) | (5, 3) | 20 | 10 | 10 | 1 | 0 |
Answer
Since the distance between data \(\small D\) and \(\small E\) is 1, which is the minimum, \(\small (DE)\) is the first cluster, and the distance between cluster \(\small (DE)\) and the remaining data is calculated using the complete linkage method, and the distance matrix is modified as follows.
\( \small \qquad d((DE), A) = max(d(D,A), d(E,A)) = max(13, 20) = 20 \)
\( \small \qquad d((DE), B) = max(d(D,B), d(E,B)) = max(5, 10) = 10 \)
\( \small \qquad d((DE), C) = max(d(D,C), d(E,C)) = max(9, 10) = 10 \)
| Table 8.2.5 Modified distance matrix with cluster \(\small (DE)\) using the complete linkage | ||||
|---|---|---|---|---|
| Distance/th> | ||||
| Cluster | \(\small A\) | \(\small B\) | \(\small C\) | \(\small (DE)\) |
| \(\small A\) | 0 | |||
| \(\small B\) | 2 | 0 | ||
| \(\small C\) | 10 | 8 | 0 | |
| \(\small (DE)\) | 20 | 10 | 10 | 0 |
Here, the minimum distance is \(\small d(A,B)\) = 2, so \(\small (AB)\) becomes the next cluster. If we calculate the distance between clusters \(\small (AB)\) and \(\small C\) , \(\small (DE)\) using the complete linkage method and modify the distance matrix, we get the following.
\( \small \qquad d((AB), C) = max(d(A,C), d(B,C)) = max(10, 8) = 10 \)
\( \small \qquad d((AB), (DE)) = max(d(A, (DE)), d(B,(DE)) = max(20, 10) = 20 \)
| Table 8.2.6 Modified distance matrix with cluster \(\small (AB)\) using the complete linkage | ||||
|---|---|---|---|---|
| Distance | ||||
| Cluster | \(\small (AB)\) | \(\small C\) | \(\small (DE)\) | |
| \(\small (AB)\) | 0 | |||
| \(\small C\) | 10 | 0 | ||
| \(\small (DE)\) | 20 | 10 | 0 | |
Here, the minimum distance is \(\small d((AB), C)\) = \(\small d(C, (DE))\) = 10, so \(\small (AB)C\) or \(\small C(DE)\) becomes the next cluster. Let's select \(\small C(DE)\) is the next cluster. If we calculate the distance between clusters \(\small (AB)\) using the complete linkage method, we get the following.
\( \small \qquad d((AB), C(DE)) = max(d((AB), C), d((AB), (DE))) = max(10, 20) = 20 \)
If the above complete linkage method is displayed as a dendrogram, it is as shown in <Figure 8.2.4>.

C. Average linkage
| Table 8.2.7 Five observed data and the matrix of squared Euclid distances | ||||||
|---|---|---|---|---|---|---|
| Distance/th> | ||||||
| Data | \(\small (x_{1}, \small x_{2})\) | \(\small A\) | \(\small B\) | \(\small C\) | \(\small D\) | \(\small E\) |
| \(\small A\) | (1, 5) | 0 | ||||
| \(\small B\) | (2, 4) | 2 | 0 | |||
| \(\small C\) | (4, 6) | 10 | 8 | 0 | ||
| \(\small D\) | (4, 3) | 13 | 5 | 9 | 0 | |
| \(\small E\) | (5, 3) | 20 | 10 | 10 | 1 | 0 |
Answer
Since the distance between data \(\small D\) and \(\small E\) is 1, which is the minimum, \(\small (DE)\) is the first cluster, and the distance between cluster \(\small (DE)\) and the remaining data is calculated using the average linkage method, and the distance matrix is modified as follows.
\( \small \qquad d((DE), A) = \frac{d(D,A) + d(E,A)}{2 \times 1} = \frac {13 + 20}{2} = 16.5 \)
\( \small \qquad d((DE), B) = \frac{d(D,B) + d(E,B)}{2 \times 1} = \frac {5 + 10}{2} = 7.5 \)
\( \small \qquad d((DE), C) = \frac{d(D,C) + d(E,C)}{2 \times 1} = \frac {9 + 10}{2} = 9.5 \)
| Table 8.2.8 Modified distance matrix with cluster \(\small (DE)\) using the single linkage | ||||
|---|---|---|---|---|
| Distance/th> | ||||
| Cluster | \(\small A\) | \(\small B\) | \(\small C\) | \(\small (DE)\) |
| \(\small A\) | 0 | |||
| \(\small B\) | 2 | 0 | ||
| \(\small C\) | 10 | 8 | 0 | |
| \(\small (DE)\) | 16.5 | 7.5 | 9.5 | 0 |
Here, the minimum distance is \(\small d(A,B)\) = 2, so \(\small (AB)\) becomes the next cluster. If we calculate the distance between clusters \(\small (AB)\) and \(\small C\) , \(\small (DE)\) using the average linkage method and modify the distance matrix, we get the following.
\( \small \qquad d((AB), C) = \frac{d(A,C) + d(B,C)}{2 \times 1} = \frac{10 + 8}{2} = 9 \)
\( \small \qquad d((AB), (DE)) = \frac{d(A,D) + d(A,E) + d(B,D) + d(B,E)}{2 \times 2} = \frac{13+20+5+10}{4} = 12 \)
| Table 8.2.9 Modified distance matrix with cluster \(\small (AB)\) using the average linkage | ||||
|---|---|---|---|---|
| Distance/th> | ||||
| Cluster | \(\small (AB)\) | \(\small C\) | \(\small (DE)\) | |
| \(\small (AB)\) | 0 | |||
| \(\small C\) | 9 | 0 | ||
| \(\small (DE)\) | 12 | 9.5 | 0 | |
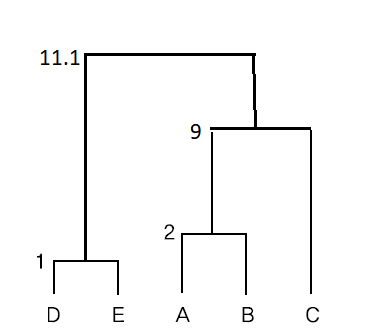
Here, the minimum distance is \(\small (d(AB), C)\) = 9, so \(\small (AB)C\) becomes the next cluster. If we calculate the distance between clusters \(\small (AB)C\) and \(\small (DE)\) using the average linkage method, we get the following.
\( \small \qquad d((AB)C, (DE)) = \frac{d(A,D)+d(A,E)+d(B,D)+d(B,E)+d(C,D)+d(C,E)}{3 \times 2} = \frac{12+20+5+10+9+10}{6} = 11.1 \)
If the above average linkage method is displayed as a dendrogram in <Figure 8.2.5>.
D. Centroid linkage
| Table 8.2.10 Five observed data and the matrix of squared Euclid distances | ||||||
|---|---|---|---|---|---|---|
| Distance/th> | ||||||
| Data | \(\small (x_{1}, \small x_{2})\) | \(\small A\) | \(\small B\) | \(\small C\) | \(\small D\) | \(\small E\) |
| \(\small A\) | (1, 5) | 0 | ||||
| \(\small B\) | (2, 4) | 2 | 0 | |||
| \(\small C\) | (4, 6) | 10 | 8 | 0 | ||
| \(\small D\) | (4, 3) | 13 | 5 | 9 | 0 | |
| \(\small E\) | (5, 3) | 20 | 10 | 10 | 1 | 0 |
Answer
Since the distance between data \(\small D\) and \(\small E\) is 1, which is the minimum, \(\small (DE)\) is the first cluster, and the distance between cluster \(\small (DE)\) and the remaining data is calculated using the centroid linkage method, and the distance matrix is modified as follows.
\( \small \qquad d((DE), A) = (4.5 - 1)^2 + (3-5)^2 = 16.25 \)
\( \small \qquad d((DE), B) = (4.5 - 2)^2 + (3-4)^2 = 7.25 \)
\( \small \qquad d((DE), C) = (4.5 - 4)^2 + (3-6)^2 = 9.25 \)
| Table 8.2.11 Modified distance matrix with cluster \(\small (DE)\) using the centroid linkage | ||||
|---|---|---|---|---|
| Distance/th> | ||||
| Cluster | \(\small A\) | \(\small B\) | \(\small C\) | \(\small (DE)\) |
| \(\small A\) | 0 | |||
| \(\small B\) | 2 | 0 | ||
| \(\small C\) | 10 | 8 | 0 | |
| \(\small (DE)\) | 16.25 | 7.25 | 9.25 | 0 |
Here, the minimum distance is \(\small d(A,B)\) = 2, so \(\small (AB)\) becomes the next cluster and the center of the cluster is \(\small \frac{(4,3) + (5,3)}{2} = (4.5, 3)\). If we calculate the distance between clusters \(\small (AB)\) and \(\small C\) , \(\small (DE)\) using the centroid linkage method and modify the distance matrix, we get the following.
\( \small \qquad d((AB), C) = (1.5 - 4)^2 + (4.5 - 6)^2 = 8.5 \)
\( \small \qquad d((AB), (DE)) = (1.5 - 4.5)^2 + (4.5 - 3)^2 = 11.25 \)
| Table 8.2.12 Modified distance matrix with cluster \(\small (AB)\) using the centroid linkage | ||||
|---|---|---|---|---|
| Distance/th> | ||||
| Cluster | \(\small (AB)\) | \(\small C\) | \(\small (DE)\) | |
| \(\small (AB)\) | 0 | |||
| \(\small C\) | 8.5 | 0 | ||
| \(\small (DE)\) | 11.25 | 9.5 | 0 | |
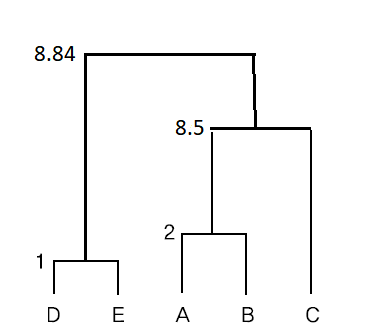
Here, the minimum distance is \(\small (d(AB), C))\) = 8.5, so \(\small (AB)C\) becomes the next cluster and the center of the cluster is as follows.
\( \qquad \frac{2 \times (1.5, \; 4.5) + 1 \times (4, \; 6)}{2 + 1} \) = (2.3, 5)
If we calculate the distance between clusters \(\small (AB)C\) and \(\small (DE)\) using the centroid linkage method, we get the following.
\( \small \qquad d((AB)C, (DE)) = (2.3 - 4.5)^2 + (5-3)^2 \) = 8.84
If the above centroid linkage method is displayed as a dendrogram as shown in <Figure 8.2.6>.
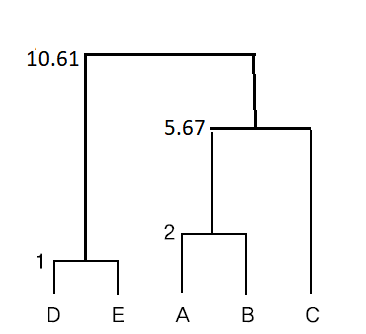
E. Ward linkage
\( \small \qquad ESS_{i} = \sum_{j=1}^{n_{i}} \; \sum_{k=1}^{m} \; (x_{ijk} - \overline x_{ik} )^2 \)
\( \small \qquad ESS = \sum_{i=1}^{K} \; ESS_{i} = \sum_{i=1}^{K} \; \sum_{j=1}^{n_{i}} \; \sum_{k=1}^{m} \; (x_{ijk} - \overline x_{ik} )^2 \)
First, each data itself forms a cluster, then, since \(ESS_{i}\) for all i, \(ESS\) = 0. At each stage of creating a cluster, the merging of all possible pairs of clusters is considered, and the clusters are merged to create a new cluster so that the increment of \(ESS\) (information loss) due to the merging of two clusters is minimized. The increment of \(ESS\) that occurs when grouping two clusters \(\small G_{i}\) and \(\small G_{j}\), whose sizes are \(n_{i}\) and \(n_{j}\) respectively, is as follows, and the Ward linkage method defines this increment as the distance between the two clusters \(\small G_{i}\) and \(\small G_{j}\). $$ \small \qquad d(G_{i}, G_{j}) = \frac{|| \boldsymbol c_{i} - \boldsymbol c_{j} ||^2 }{\frac{1}{n_{i}} + \frac{1}{n_{j}} } $$ Here, \( \boldsymbol c_{i}\) and \( \boldsymbol c_{j} \) are the averages of two clusters \(\small G_{i}\) and \(\small G_{j}\) respectively. This result differs from the centroid linkage method because the Ward linkage weights the distance between clusters means when calculating the distance between clusters. The Ward linkage method tends to merge clusters of similar size.
| Table 8.2.13 Five observed data and the matrix of squared Euclid distances | ||||||
|---|---|---|---|---|---|---|
| Distance/th> | ||||||
| Data | \(\small (x_{1}, \small x_{2})\) | \(\small A\) | \(\small B\) | \(\small C\) | \(\small D\) | \(\small E\) |
| \(\small A\) | (1, 5) | 0 | ||||
| \(\small B\) | (2, 4) | 2 | 0 | |||
| \(\small C\) | (4, 6) | 10 | 8 | 0 | ||
| \(\small D\) | (4, 3) | 13 | 5 | 9 | 0 | |
| \(\small E\) | (5, 3) | 20 | 10 | 10 | 1 | 0 |
Answer
When each data is considered as a cluster, the increment of ESS is the squared Euclid distance. Since the distance between data D and E is 1, which is the minimum, (DE) becomes the first cluster. The center of the cluster (DE) is \( \frac{(4,3) + (5,3)}{2} \) = (4.5, 3), so the distance is calculated using the Ward linkage method for the remaining data, and the distance matrix is modified as follows.
\( \small \qquad d((DE), A) = \frac{(4.5 - 1)^2 + (3 - 5)^2)}{\frac{1}{2} +\frac{1}{1}} = 11.17 \)
\( \small \qquad d((DE), B) = \frac{(4.5 - 2)^2 + (3 - 4)^2)}{\frac{1}{2} +\frac{1}{1}} = 4.83 \)
\( \small \qquad d((DE), C) = \frac{(4.5 - 4)^2 + (3 - 6)^2)}{\frac{1}{2} +\frac{1}{1}} = 6.17 \)
| Table 8.2.14 Modified distance matrix with cluster \(\small (DE)\) using the Ward linkage | ||||
|---|---|---|---|---|
| Distance/th> | ||||
| Cluster | \(\small A\) | \(\small B\) | \(\small C\) | \(\small (DE)\) |
| \(\small A\) | 0 | |||
| \(\small B\) | 2 | 0 | ||
| \(\small C\) | 10 | 8 | 0 | |
| \(\small (DE)\) | 11.17 | 4.83 | 6.17 | 0 |
Here, the minimum distance is \(\small d(A,B)\) = 2, so \(\small (AB)\) becomes the next cluster and the center of the cluster becomes \( \frac{(1,5) + (2,4)}{2} \) = (1.5, 4.5). If we calculate the distance between clusters \(\small (AB)\) and \(\small C\) , \(\small (DE)\) using the Ward linkage method and modify the distance matrix, we get the following.
\( \small \qquad d((AB), C) = \frac{(1.5 - 4)^2 + (4.5 - 6)^2)}{\frac{1}{2} +\frac{1}{1}} = 5.67 \)
\( \small \qquad d((AB), (DE)) = \frac{(1.5 - 4.5)^2 + (4.5 - 3)^2)}{\frac{1}{2} +\frac{1}{1}} = 11.25 \)
| Table 8.2.15 Modified distance matrix with cluster \(\small (AB)\) using the Ward linkage | ||||
|---|---|---|---|---|
| Distance/th> | ||||
| Cluster | \(\small (AB)\) | \(\small C\) | \(\small (DE)\) | |
| \(\small (AB)\) | 0 | |||
| \(\small C\) | 5.67 | 0 | ||
| \(\small (DE)\) | 11.25 | 6.17 | 0 | |
Here, the minimum distance is \(\small (d(AB), C)\) = 5.67, so \(\small (AB)C\) becomes the next cluster and the center of the cluster becomes \( \frac{2 \times (1.5, 4.5) + 1 \times (4, 6)}{2 + 1} \) = (2.3, 5). If we calculate the distance between clusters \(\small (AB)C)\) and \(\small DE\) using the Ward linkage method, we get the following.
\( \small \qquad d((AB)C, (DE)) = \frac{(2.3 - 4.5)^2 + (5 - 3)^2)}{\frac{1}{3} +\frac{1}{2}} = 10.61 \)
If the above Ward linkage method is displayed as a dendrogram, it is as shown in <Figure 8.2.7>.
[Hierarchical clustering\
Characteristics of the hierarchical clustering model
8.2.2 R and Python practice - Hierarchical clustering
R practice
[Colab]
| Distance Matrix Computation This function computes and returns the distance matrix computed by using the specified distance measure to compute the distances between the rows of a data matrix. |
|
|---|---|
| dist(x, method = "euclidean", diag = FALSE, upper = FALSE, p = 2) | |
| x | a numeric matrix, data frame or "dist" object. |
| method | the distance measure to be used. This must be one of "euclidean", "maximum", "manhattan", "canberra", "binary" or "minkowski". |
| diag | logical value indicating whether the diagonal of the distance matrix should be printed by print.dist. |
| upper | logical value indicating whether the upper triangle of the distance matrix should be printed by print.dist. |
| p | The power of the Minkowski distance. |
| hclust {stats} | Hierarchical Clustering Hierarchical cluster analysis on a set of dissimilarities and methods for analyzing it. |
|---|---|
| hclust(d, method = "complete", members = NULL) | |
| d | a dissimilarity structure as produced by dist. |
| members | NULL or a vector with length size of d. |
An example of R commands for a Hierarchical clustering with 30 iris data is as follows.
| library(stats) |
| iris <- read.csv('http://estat.me/estat/Example/DataScience/Iris30.csv', header=T, as.is=FALSE) |
| attach(iris) |
|
# select Sepal.Length, Sepal.Width, Petal.Length, Petal.Width from iris data iris4 <- iris[, c(2,3, 4, 5)] |
|
# calculate distance matrix using squared Euclid distance dist(iris4, method = 'euclidean') |
| hclustIris4 <-hclust(distIris4, method = "ward.D") |
hclustIris4
Call: hclust(d = distIris4, method = "ward.D") Cluster method : ward.D Distance : euclidean Number of objects: 30 |
| # plot hierarchical clusters plot(hclustIris4) 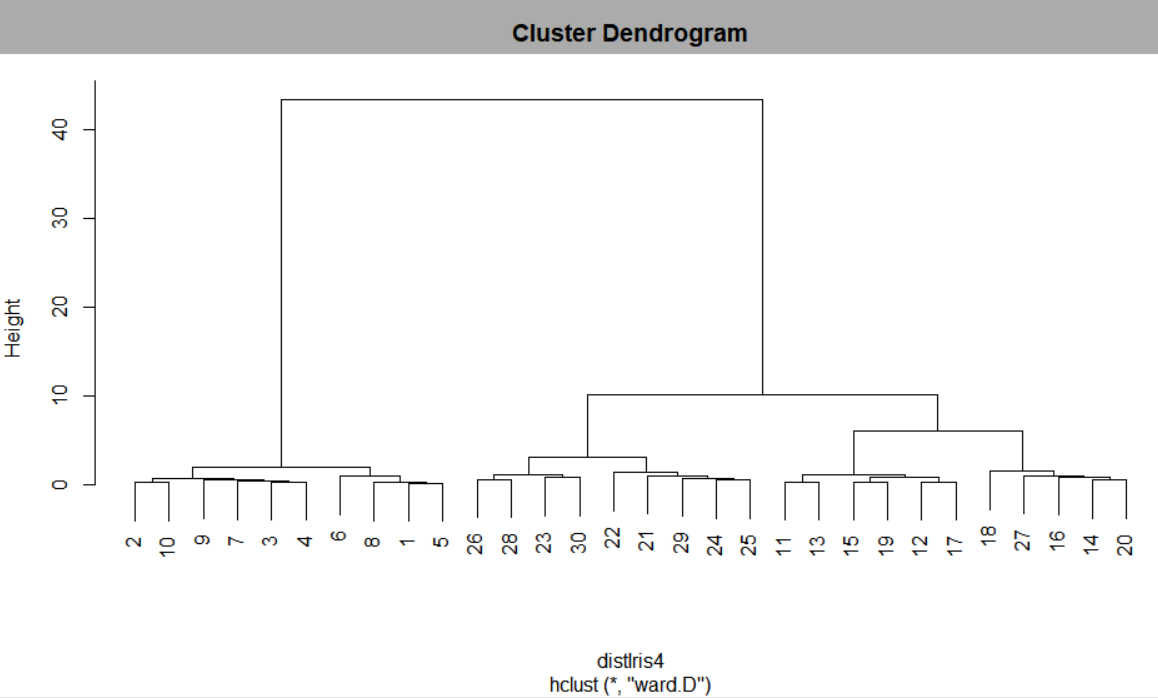
<Figure 8.2.8> Hierarchical clustering dendrogram using R
|
Python practice
[Colab]
|
# Import required libraries import pandas as pd import numpy as np from scipy.cluster.hierarchy import dendrogram, linkage from scipy.spatial.distance import pdist import matplotlib.pyplot as plt from sklearn.datasets import load_iris # Load iris dataset iris = load_iris() iris_df = pd.DataFrame(data=iris.data, columns=iris.feature_names) # Select the four features (equivalent to Sepal.Length, Sepal.Width, Petal.Length, Petal.Width) iris4 = iris_df.iloc[:, [0, 1, 2, 3]] # Calculate distance matrix using squared Euclidean distance dist_matrix = pdist(iris4, metric='euclidean') # Perform hierarchical clustering using Ward's method hclust = linkage(dist_matrix, method='ward') # Plot dendrogram plt.figure(figsize=(10, 6)) dendrogram(hclust, labels=iris_df.index) plt.title('Hierarchical Clustering Dendrogram (Ward)') plt.xlabel('Sample Index') plt.ylabel('Distance') plt.show() 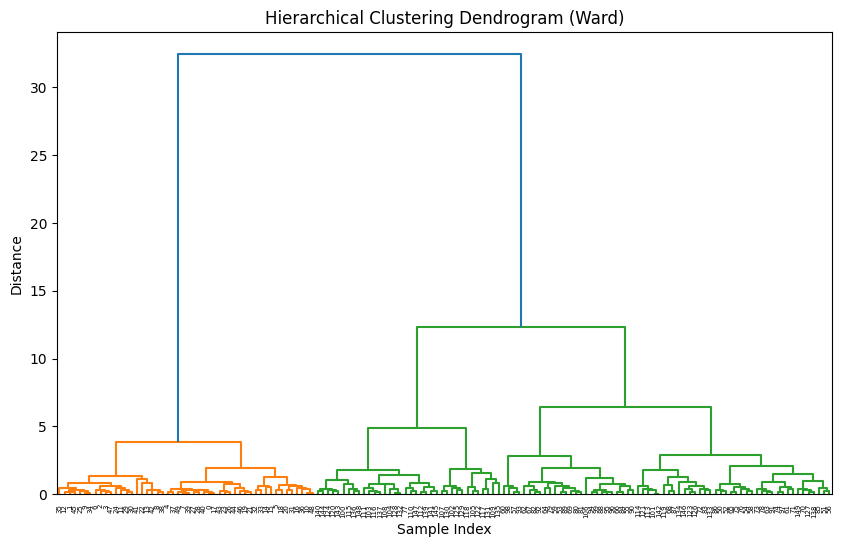
|
8.3 \(\small K\)-means clustering model
The clustering model requires an appropriate distance measure between data and a cluster. \(\small K\)-means clustering model first determines the number of clusters \(\small K\) and selects the initial center of each cluster. Then, each data is classified into a cluster with the closest cluster center, and the center of each cluster is recalculated. We can use the various distance measures studied in Chapter 2, and in the case of continuous data, the Euclidean distance is generally used. This method is repeated until there is no change in the cluster center. The basic procedure of the \(\small K\)-means clustering model is summarized as follows.
| Step 1 | Determine the number of clusters \(\small K\) you want. |
| Step 2 | Select the initial center of each cluster. |
| Step 3 | repeat |
| Step 4 | \(\qquad\)Classify each data into the cluster with the closest cluster center. |
| Step 5 | \(\qquad\)Recalculate the center of each cluster. |
| Step 6 | until (there is little change in the cluster center |
| Table 8.3.1 Data for the 2-means clustering algorithm | |
|---|---|
| Data | (\(x_{1}, x_{2}\)) |
| A | (3, 4) |
| B | (-1, 2) |
| C | (-2, -3) |
| D | (1, -2) |
Answer
Let the center of cluster 1 be data A=(3,4) and the center of cluster 2 be data C=(-2,-3). The distances from each data to the centers of the two clusters are as follows.
| Table 8.3.2 Distance between data and the center of cluster | ||
|---|---|---|
| Data | Cluster 1 Distance to center (3, 4) |
Cluster 2 Distance to center (-2, -3) |
| A | 0 | 74 |
| B | 20 | 26 |
| C | 74 | 0 |
| D | 40 | 10 |
Therefore, if each data is classified by the nearest cluster center, data A and B are classified into cluster 1, data C and D are classified into cluster 2, and the center of the new cluster 1 by the average is (1,3), and the center of cluster 2 is (-0.5,-2.5). The distances from each data to the centers of the two new clusters are as follows.
| Table 8.3.3 Modified distance between data and the center of cluster | ||
|---|---|---|
| Data | Cluster 1 Distance to center (1, 3) |
Cluster 2 Distance to center (-0.5, -2.5) |
| A | 5 | 54.5 |
| B | 5 | 20.5 |
| C | 45 | 2.5 |
| D | 25 | 2.5 |
If each data is classified by the nearest cluster center, data A and B are classified again as cluster 1, and data C and D are classified as cluster 2, so the center of each cluster does not change, so the algorithm is stopped. Finally, data A and B are classified as cluster 1, and data C and D are classified as cluster 2.
Theoretical background of the \(\small K\)-means clustering model
Suppose there are \(m\) variables \(\small \boldsymbol x = (x_{1}, x_{2}, ... , x_{m}) \) and \(n\) number of data observed for these variables. Let the \(\small K\) clusters be \(\small G_{1}, G_{2}, ... , G_{K}\), the number of data observed in each cluster be \(\small n_{1}, n_{2}, ... , n_{K}\), and the mean of each cluster be \(\small \boldsymbol c_{1}, \boldsymbol c_{2}, ... , \boldsymbol c_{K} \) as follows. $$ \boldsymbol c_{i} = \frac{1}{n_{i}} \; \sum_{\boldsymbol x \in G_{i}} \; \boldsymbol x $$ If \(\small d(\boldsymbol c_{i}, \boldsymbol x)\) is the distance between the center \(\small \boldsymbol c_{i}\) of cluster \(\small G_{i}\) and the data \(\small \boldsymbol x\), the measure of cluster performance can be defined as the sum of distances from all data to each center. $$ \text{(Performance measure of clustering)} = \sum_{i=1}^{K} \; \sum_{\boldsymbol x \in G_{i}} \; d( \boldsymbol c_{i} , \boldsymbol x) $$ When using the squared Euclid distance as a distance measure, the \(\small \boldsymbol c_{i}\) that minimizes this performance measure of clustering can be shown to be the mean of the cluster. Here, let us prove that \(\small \boldsymbol c_{i}\) is the cluster's mean when the data is only one-dimensional. The performance measure of clustering is the following within sum of squares (WSS) in the case of the squared Euclid distance. $$ \text{WSS} = \sum_{i=1}^{K} \; \sum_{x \in G_{i}} \; (c_{i} - x)^2 $$ In order to find \(\small c_{1}, c_{2}, ... , c_{K} \) that minimizes this WSS, we take partial differentiation for each \(\small c_{i}, i=1,2, ... , K\), and set it to 0. $$ \frac{\partial}{\partial c_{i}} \text{SSE} = \sum_{x \in G_{i}} \; 2 (c_{i} - x) = 0 $$ The solution to these simultaneous equations is as follows. $$ c_{i} = \frac{1}{n_{i}} \; \sum_{x \in G_{i}} \; x $$ That is, \(\small c_{1}, c_{2}, ... , c_{K} \) that minimize the SSE are each mean of the clusters.
If the data is one-dimensional and the absolute distance (Manhattan distance) is used as a distance measure, the performance measure of clustering becomes the sum of absolute error (SAE) as follows. $$ \text{SAE} = \sum_{i=1}^{K} \; \sum_{x \in G_{i}} \; | c_{i} - x | $$ It can be shown that the solution \(\small c_{1}, c_{2}, ... , c_{K} \) that minimizes this SAE are each median of the clusters. In general, the median is known to be less sensitive to extreme points or outliers.
Determine the number of cluster
\(\small K\)-means clustering module of 『eStatU』 provides a plot of the within sum of squares for various \(\small K\) as follows. After selecting \(\small K\), you can do clustering analysis by checking 'fixed K'.
8.3.1 R and Python practice - \(\small K\)-means clustering
R practice
[Colab]
| \(\small K\)-Means Clustering Perform k-means clustering on a data matrix. |
|
|---|---|
| kmeans(x, centers, iter.max = 10, nstart = 1, algorithm = c("Hartigan-Wong", "Lloyd", "Forgy", "MacQueen"), trace = FALSE) | |
| x | numeric matrix of data, or an object that can be coerced to such a matrix (such as a numeric vector or a data frame with all numeric columns). |
| centers | either the number of clusters, say k, or a set of initial (distinct) cluster centres. If a number, a random set of (distinct) rows in x is chosen as the initial centres. |
| test | The data set for which we want to obtain the k-NN classification, i.e. the test set. |
| iter.max | the maximum number of iterations allowed. |
| nstart | if centers is a number, how many random sets should be chosen? |
An example of R commands for a \(\small K\)-means clustering with iris data when k = 3 is as follows.
| library(stats) |
| iris <- read.csv('http://estat.me/estat/Example/DataScience/Iris150.csv', header=T, as.is=FALSE) |
| attach(iris) |
|
# select Sepal.Length, Sepal.Width, Petal.Length, Petal.Width from iris data iris4 <- iris[, c(2,3, 4, 5)] |
| iriskmeans <- kmeans(iris4, centers = 3, iter.max = 1000) |
iriskmeans
K-means clustering with 3 clusters of sizes 38, 62, 50 Cluster means: Sepal.Length Sepal.Width Petal.Length Petal.Width 1 6.850000 3.073684 5.742105 2.071053 2 5.901613 2.748387 4.393548 1.433871 3 5.006000 3.428000 1.462000 0.246000 Clustering vector: [1] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 [38] 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 [75] 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 1 1 1 1 2 1 1 1 1 [112] 1 1 2 2 1 1 1 1 2 1 2 1 2 1 1 2 2 1 1 1 1 1 2 1 1 1 1 2 1 1 1 2 1 1 1 2 1 [149] 1 2 Within cluster sum of squares by cluster: [1] 23.87947 39.82097 15.15100 (between_SS / total_SS = 88.4 %) Available components: [1] "cluster" "centers" "totss" "withinss" "tot.withinss" [6] "betweenss" "size" "iter" "ifault" |
| # the cluster vector only can be seen as follows. 1: verginica, 2: versicolor, 3: setosa iriskmeans$cluster [1] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 [38] 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 [75] 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 1 1 1 1 2 1 1 1 1 [112] 1 1 2 2 1 1 1 1 2 1 2 1 2 1 1 2 2 1 1 1 1 1 2 1 1 1 1 2 1 1 1 2 1 1 1 2 1 [149] 1 2 |
To make a classification cross table, you can use a vector of Species and iriskmeans$cluster which is the cluster with table command as below. 'Setosa's are clustered 100% correctly, 'versicolor's are 48/50, but 'virginica's are 36/50.
|
# 1: verginica, 2: versicolor, 3: setosa classtable <- table(Species, iriskmeans$cluster) Species 1 2 3 setosa 0 0 50 versicolor 2 48 0 virginica 36 14 0 |
Python practice
[Colab]
|
# Import required libraries import pandas as pd import numpy as np from sklearn.datasets import load_iris from sklearn.cluster import KMeans # Load iris dataset iris = load_iris() iris_df = pd.DataFrame(data=iris.data, columns=iris.feature_names) iris_df['Species'] = pd.Categorical.from_codes(iris.target, iris.target_names) # Select the four features (Sepal Length, Sepal Width, Petal Length, Petal Width) iris4 = iris_df.iloc[:, [0, 1, 2, 3]] # Perform k-means clustering kmeans = KMeans(n_clusters=3, max_iter=1000, random_state=123) iriskmeans = kmeans.fit(iris4) # Get cluster assignments cluster_labels = iriskmeans.labels_ # Print k-means resultsv print("K-means clustering results:") print(f"Cluster centers:\n{iriskmeans.cluster_centers_}") print(f"Cluster assignments:\n{cluster_labels}") # Create classification table (cross-tabulation of Species and clusters) classtable = pd.crosstab(iris_df['Species'], cluster_labels, rownames=['Species'], colnames=['Cluster']) print("\nClassification table:") print(classtable) K-means clustering results: Cluster centers: [[6.85 3.07368421 5.74210526 2.07105263] [5.006 3.428 1.462 0.246 ] [5.9016129 2.7483871 4.39354839 1.43387097]] Cluster assignments: [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 0 0 0 0 2 0 0 0 0 0 0 2 2 0 0 0 0 2 0 2 0 2 0 0 2 2 0 0 0 0 0 2 0 0 0 0 2 0 0 0 2 0 0 0 2 0 0 2] Classification table: Cluster 0 1 2 Species setosa 0 50 0 versicolor 2 0 48 virginica 36 0 14 |
8.4 Exercise
8.1 The distance matrix for five data (A, B, C, D, E) is as follows.
| Distance | A | B | C | D | E |
|---|---|---|---|---|---|
| A | 0 | ||||
| B | 10 | 0 | |||
| C | 41 | 64 | 0 | ||
| D | 55 | 47 | 44 | 0 | |
| E | 35 | 98 | 85 | 76 | 0 |
8.2 The following six data were observed for two variables \(X_1\) and \(X_2\).
| Data | \(X_1\) | \(X_2\) |
|---|---|---|
| A | 3 | 4 |
| B | -1 | 2 |
| C | -2 | -3 |
| D | 1 | -2 |
| E | 1 | 3 |
| E | -1 | 2 |
8.3 Create clusters using the 2-mean clustering model. Use the mean as the central measure in the data of Problem 2.