Chapter 6. Supervised machine learning for categorical data
[presentation] [book]
- 6.1 Basic concepts of supervised machine learning and classification
- 6.1.1 Evaluation measures of classification model
- 6.1.2 Spliting method for training and testing data
- 6.2 Decision tree model
- 6.2.1 Decision tree algorithm
- 6.2.2 Selection of a variable for branching
- 6.2.3 Categorization of a continuous variable
- 6.2.4 Overfitting and pruning decision tree
- 6.2.5 R and Python practice - Decision tree
- 6.3 Naive Bayes classification model
- 6.3.1 Bayes classification model
- 6.3.2 Naive Bayes classification model for categorical data
- 6.3.3 Stepwise variable selection
- 6.3.4 R and Python practice - Naive Bayes classification
- 6.4 Evaluation and comparison of classification model
- 6.4.1 Evaluation of classification model
- 6.4.2 Comparison of classification models
- 6.5 Exercise
CHAPTER OBJECTIVES
6.1 Basic concepts of supervised machine learning and classification
A standard method to classify data whose group affiliation is unknown into a group would be to classify it into the group that is the ‘closest’ to that data. Many methods define 'closeness' as being from one data source to a group. For example, the Euclid distance from the data to the mean of each group, the Minkowski distance, or the Mahalanobis distance, a statistical measure that considers the variance of the data, can be used. If we consider a probabilistic approach, there may be a method to estimate the distribution function of each group and classify data whose group affiliation is unknown into the group it is likely to belong to. There are many classification models based on various reasonable criteria. In this chapter, we focus on statistical models for discrete data, such as the decision tree model and the naive Bayes classification model. Chapter 7 discusses other classification models for continuous data, such as the k-nearest neighbor model, the neural network model, the support vector machine model, and the ensemble model.
Classification analysis procedure
|
Data cleaning and division Collect data from each group, clean and transform it, and divide the data into training and test data. |
| ↓ ↑ |
|
Training the model Establish a classification model \(y = f( \boldsymbol x ) \) using the training data. |
| ↓ ↑ |
|
Validation of the model Validate the classification model using the testing data. |
| ↓ |
|
Apply the model Classify data whose group affiliation is unknown into one group using the classification model. |
First, data is collected, refined, and transformed appropriately for analysis. Then, the observed data in each group is divided into training data and testing data. Using the training data, establish a classification model \(y = f( \boldsymbol x ) \) where \(y\) is the target variable to be estimated, which means the group. The validity of the model is examined using the testing data. If this model is not satisfactory, another model is established again, and its validity is examined. After comparing several classification models and selecting the most satisfactory classification model, this model is applied to data whose group is unknown to determine which group to classify. If the variable that represents each group is considered as a dependent variable and the variable used to classify each group is considered as an independent variable, classification analysis is similar to regression analysis. However, in regression analysis, the dependent variable is a random variable that follows a normal distribution, and the levels of the independent variables are assumed to be given constants, but classification analysis does not make this assumption, so there is a difference in the model.
Preparation of data for classification analysis
A. Data cleaning
If there is noise in the data, it is recommended to remove it. If there are missing values, it is recommended to preprocess using the corresponding variable's average or mode.B. Relevance analysis
Among the variables in the data, there may be variables that are not related to classification, or the variables may be duplicated. Relevance analysis can be used to remove irrelevant or duplicated variables, improving the classification model's efficiency and accuracy.C. Data transformation
Continuous data may need to be discretized for classification. The neural network model requires converting the units of variable values, such as from -1.0 to 1.0 or from 0.0 to 1.0.
6.1.1 Evaluation measures of classification model
| Table 6.1.1 Table for the test results of the actual group and the classified group | ||||
|---|---|---|---|---|
| Classified group | ||||
| \(\small G_1\) | \(\small G_2\) | Total | ||
| Actual group | \(\small G_1\) | \(\small f_{11}\) | \(\small f_{12}\) | \(\small f_{11} + f_{12}\) |
| \(\small G_2\) | \(\small f_{21}\) | \(\small f_{22}\) | \(\small f_{21} + f_{22}\) | |
| Total | \(n\) | |||
Here, \(f_{ij}\) means the number of data of the group \(G_i\) classified into the group \(G_j\). The number of data correctly classified out of the total data is \(f_{11} + f_{22}\), and the number of data incorrectly classified is \(f_{12} + f_{21}\). The accuracy of the classification model is defined as the ratio of the number of correctly classified data out of the total number of data, and the error rate is defined as the ratio of the number of incorrectly classified data out of the total number of data. $$ \begin{align} \text{Accuracy} &= \frac{f_{11} + f_{22}}{n} \\ \text{Error rate} &= \frac{f_{12} + f_{21}}{n} \end{align} $$
Generally, classification models strive to find an algorithm that maximizes accuracy or minimizes error rate. Accuracy and error rate are reasonable criteria assuming that each data belongs to one group. However, there is a possibility that one data belongs to more than one group, in which case it is reasonable to predict the probability of belonging to the group. There are various measures other than accuracy and error rate to evaluate a classification model, and lift charts, ROC graphs, and statistical analysis methods are used to compare and evaluate various classification models, which are explained in detail in Section 6.4.
6.1.2 Spliting method for training and testing data
A. Holdout Method and Random Subsampling
To solve the above problems and to increase the reliability of the accuracy of the classification model, the preliminary method can be repeatedly performed. Each non-replaced sample is called a subsampling, and the method of repeatedly extracting them is called the random subsampling method. If the accuracy of the classification model by the \(i^{th}\) subsampling is \( (Accuracy)_i\), and this experiment is repeated \(r\) times, the overall accuracy of the classification model is defined as the average of each accuracy as follows; $$ \text{Overall accuarcy} = \frac{1}{r} \Sigma_{i=1}^r (Accuracy)_i $$ Since the random subsampling method does not use the entire data set, just like the holdout method, it still has problems. However, since the accuracy of the model is repeatedly estimated, the reliability can be increased.
B. Cross Validation Method
If the two-fold cross-validation method is extended, the \(k\)-fold cross-validation method can be created. This method divides the entire data set into \(k\) equal-sized subsets, reserves one of the subsets as testing data, and uses the remaining data as training data to obtain the classification function. This method is repeated \(k\) times so that each data subset can be used for testing once. The accuracy of the classification model is the average of the measured accuracies.
In the cross-validation method, a special case where the total number of data is \(k\), that is, when there is only one testing data, is called the leave-one-out method. This method has the advantage of maximizing the training data and testing all data without overlapping the test data. However, since each testing data contains only one data, there is a disadvantage in that the variance of the estimated accuracy increases, and since the experiment must be repeated as many times as the number of data, it takes a lot of time.
C. Bootstrap method
6.2 Decision tree model
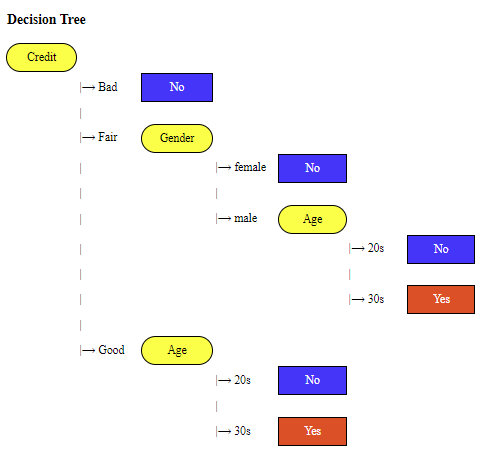
In the tree diagram above, the ovals colored yellow represent nodes that indicate tests for variables, and the top node is called the root node. In <Figure 6.2.1>, Credit is the root node, and Gender and Age are nodes for testing variables. The branches from the nodes represent the values of the tested variables, and the rectangles colored blue or red represent the final classified groups, which are called leaves. The root node, Credit, has three branches 'Bad', 'Fair', and 'Good', and the classified group for 'Bad' credit is indicated by the leaf 'No' which is the Non-purchasing group. In order to classify the data whose group is unknown, the variable values of the data are examined along the path from the root node to the leaves. For example, in <Figure 6.2.1>, a person whose 'Credit' is 'Good' and 'Age' is '30s' is classified as 'Yes', which is a Purchasing group. When the target variable is a finite number of groups, such as Purchasing group or Non-purchasing group in the example above, the tree for classification is called a decision tree. In the case of a continuous target variable, we can draw a similar decision tree based on a regression model, which is called a regression tree (Breiman et al.).
The decision tree model was first attempted by Sonquist and Morgan in 1964 and was widely used by the general public in 1973 because of Morgan and Messenger's algorithm called THAID. In 1980, Kass introduced an algorithm called CHAID based on the chi-square goodness-of-fit test, which is still widely used today. In 1982, computer scientist Quinlan introduced a decision tree algorithm called ID3 and later developed it into an algorithm called C4.5. In 1984, Breiman et al. established the theory of decision tree growth and pruning through CART. C4.5 and CART are nonparametric classification methods, but in 1988, Loh and Vanichetaku introduced FACT, a parametric approach. Recently, rather than classifying data as a single decision tree, an ensemble model that extracts multiple samples using the bootstrap method and then integrates multiple decision tree classifications based on these samples is widely used. The ensemble model is studied in Chapter 7.
6.2.1 Decision tree algorithm
TreeGrowth (\(\small E, F\))
Step 1: \(\;\;\)if stopping_condition(\(\small E, F\)) = true then
Step 2: \(\qquad\)leaf = creatNode().
Step 3: \(\qquad\)leaf.label = Classify(\(\small E\))
Step 4: \(\qquad\)return leaf
Step 5: \(\;\;\)else
Step 6: \(\qquad\)root = creatNode()
Step 7: \(\qquad\)root.test_condition = find_best_split(\(\small E, F\))
Step 8: \(\qquad\)let \(\small V\) = {\(v: v\) is a possible outcome of root.test_condition}
Step 9: \(\qquad\)for each \(\small v \in V\) do
Step 10: \(\qquad \quad\)\(\small E_v =\){ {root.test_condition(\(\small e\)) = } ∩ {\(\small e \in E\)} }
Step 11: \(\qquad \quad\)child = TreeGrowth(\(\small E_v , F\))
Step 12: \(\qquad \quad\)add child as descendent of root and label the edge(root → child) as \(v\)
Step 13: \(\qquad\)end for
Step 14: \(\;\)end if
Step 15: \(\;\)return root
6.2.2 Selection of a variable for branching
| Table 6.2.1 Crosstable of Gender by Purchase and Non-purchasing group | |||
|---|---|---|---|
| Gender | Purchasing group \(G_1\) |
Non-purchasing group \(G_2\) |
Total |
| Male | 4 | 6 | 10 |
| Female | 4 | 6 | 10 |
| Total | 8 | 12 | 20 |
| Table 6.2.2 Crosstable of Credit status by Purchase and Non-purchasing group | |||
|---|---|---|---|
| Credit Status | Purchasing group \(G_1\) |
Non-purchasing group \(G_2\) |
Total |
| Good | 7 | 3 | 10 |
| Bad | 1 | 9 | 10 |
| Total | 8 | 12 | 20 |
Answer
In the case of Gender, the ratios of the Purchasing group to the Non-purchasing group for Male and Female are 4 to 6 (40% to 60%), which is the same as the ratio of all 20 people. In the case of Credit Status, 90% of the customers are in the Non-purchasing group when the Credit Status is Bad, and 70% are in the Purchasing group when the Credit Status is Good, so there is a significant difference in the Purchase or Non-purchase ratio between Bad and Good cases. In other words, if the Credit Status of a customer is Bad, there is a high possibility that he belongs to the Non-purchasing group, and if it is Good, there is a high possibility that he belongs to the Purchasing group. So, if the Credit Status is identified, we can distinguish the Purchasing group and the Non-purchasing group can be somewhat distinguished. Therefore, if one of the two variables must be selected as a variable for branching in the decision tree, choosing the Credit Status variable is reasonable for a more accurate classification. Generally, a variable that has a lot of information for classification is selected.
A. Chi-square independence test
| Table 6.2.3 Observed frequencies of a variable \(A\) by Purchase status group | |||
|---|---|---|---|
| Variable \(A\) value |
Purchasing group \(G_1\) |
Non-purchasing group \(G_2\) |
Total |
| \(A_1\) | \(O_{11}\) | \(O_{12}\) | \(O_{1 \cdot}\) |
| \(A_1\) | \(O_{21}\) | \(O_{22}\) | \(O_{2 \cdot}\) |
| Total | \(O_{\cdot 1}\) | \(O_{\cdot 2}\) | \(O_{\cdot \cdot}\) |
| Table 6.2.4 Expected frequencies of a variable by Purchase status when they are independent | |||
|---|---|---|---|
| Variable \(A\) value |
Purchasing group \(G_1\) |
Non-purchasing group \(G_2\) |
Total |
| \(A_1\) | \(E_{11} = O_{1 \cdot} \times \frac{O_{\cdot 1}}{O_{\cdot \cdot}} \) | \(E_{12} = O_{1 \cdot} \times \frac{O_{\cdot 2}}{O_{\cdot \cdot}}\) | \(O_{1 \cdot}\) |
| \(A_1\) | \(E_{21} = O_{2 \cdot} \times \frac{O_{\cdot 1}}{O_{\cdot \cdot}}\) | \(E_{22} = O_{2 \cdot} \times \frac{O_{\cdot 2}}{O_{\cdot \cdot}}\) | \(O_{2 \cdot}\) |
| Total | \(O_{\cdot 1}\) | \(O_{\cdot 2}\) | \(O_{\cdot \cdot}\) |
The chi-square statistic of the observed frequencies in Table 6.2.3 for independence test is the sum of the squares of the differences between the observed and expected frequencies in each cell divided by the expected frequency. $$ \chi^2 = \sum_{i=1}^{2} \sum_{j=1}^{2} \frac{ (O_{ij} - E_{ij})^2}{E_{ij}} $$ This statistic follows the chi-square distribution with a degree of freedom of 1. Suppose the distribution of each group in each variable value is the same as the distribution of the entire group. In that case, the chi-square statistic becomes 0, concluding that the variables and groups are independent. Suppose the distribution of each group in each variable value is very different from the distribution of the entire group. In that case, the chi-square statistic becomes very large, and the null hypothesis that the variables and groups are independent is rejected. The stronger the degree of rejection, the better the variable is for branching.
Answer
In the crosstable of the Gender and Purchase status, the distribution of (purchasing group, non-purchasing group) in the entire data is (40%, 60%). The distributions in each Male and female are also the same at (40%, 60%), so the expected frequencies of Male and Female are (4, 6) which are the same as observed frequencies and the chi-square statistic \(\chi_{Gender}^2\)is 0 as follows. $$ \small \chi_{Credit}^2 = \frac{ (4 - 4)^2}{4} + \frac{ (6 - 6)^2}{6} +\frac{ (4 - 4)^2}{4} +\frac{ (6 - 6)^2}{6} = 0 $$ Therefore, the Gender variable and Purchase status are independent.
In the crosstable of the Credit and Purchase status, the expected frequencies for each Credit status is (4, 6), so the chi-square statistic is as follows. $$ \small \chi_{Credit}^2 = \frac{ (7 - 4)^2}{4} + \frac{ (3 - 6)^2}{6} +\frac{ (1 - 4)^2}{4} +\frac{ (9 - 6)^2}{6} = 7.5 $$ Therefore, since it is greater than the critical value of \(\small \chi_{1;\; 0.05}^2 \) = 3.841 at the significance level of 5% in the chi-square distribution with the degree of freedom of 1, the Credit variable and Purchase status are not independent. In other words, if the Credit status is known, it contains a lot of information to decide the Purchasing group and the Non-purchasing group. Therefore, the branching is selected by selecting the Credit variable rather than the Gender variable.
B. Entropy coefficient, Gini coefficient, and classification error rate
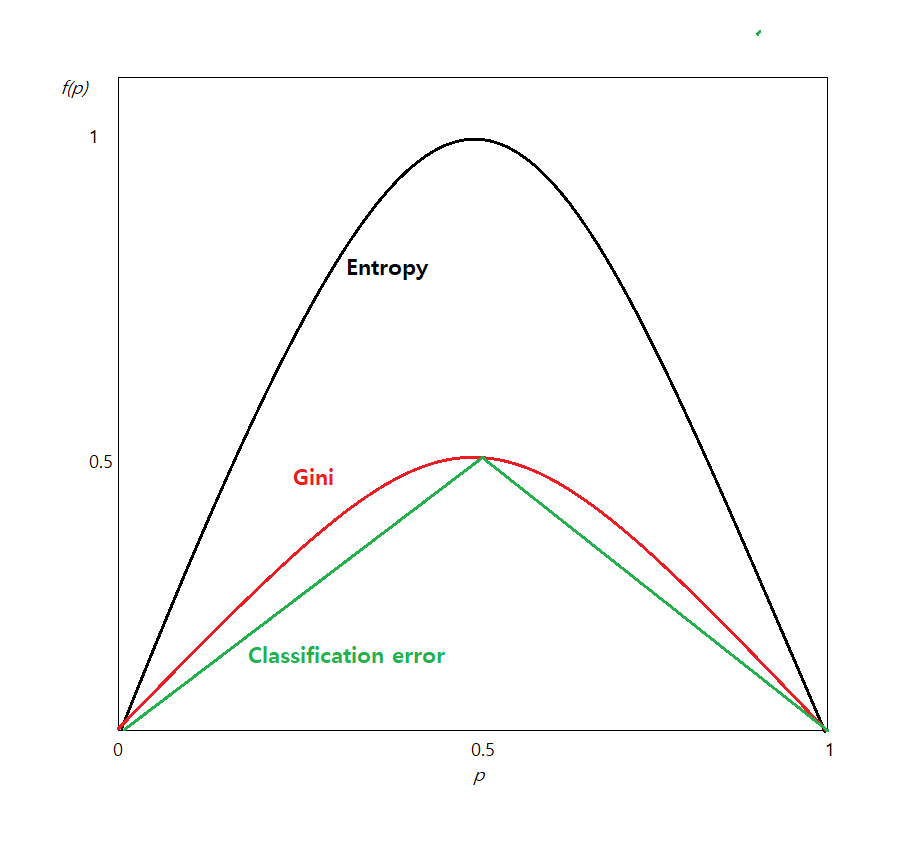
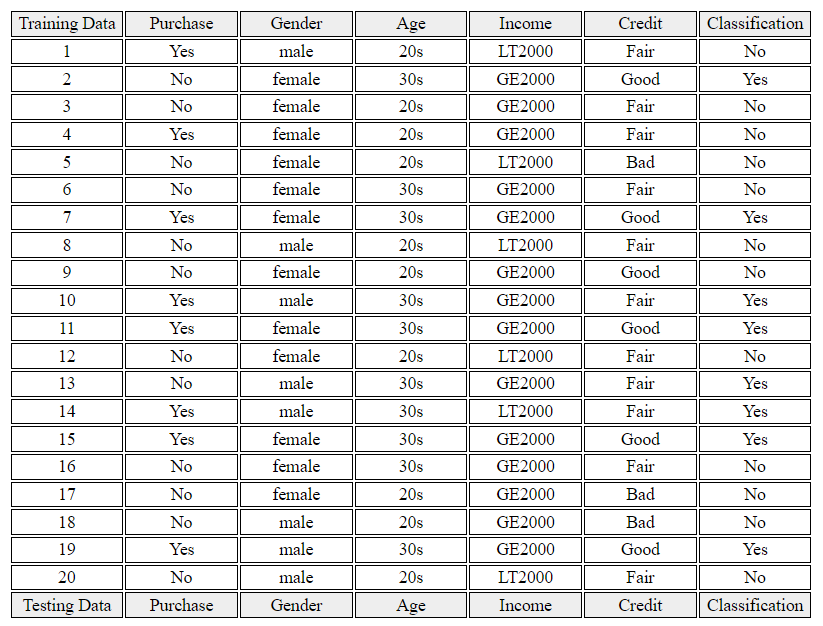
As we can see in the figure, all three measures have a maximum value when \(p\) = 0.5 (in this case, \(1-p\) = 0.5 also, and it is a uniform distribution) and a minimum value of \(p\) = 0 when or \(p\) = 1. That is, when the probability of two groups is the same (\(p\) = 0.5), uncertainty has a maximum value because we do not know which group to classify into. On the other hand, if the probability of one group is 1, there is no uncertainty, that is, the certainty of classification is 100%, so each measure has a minimum value of 0. Therefore, branching selects a variable with less uncertainty.
Answer
The entropy coefficient, Gini coefficient, and classification error rate for the probability distribution (0.4, 0.6) of the Purchasing group and the Non-purchasing group are as in Table 6.2.5, and the measures for the Gender are in Table 6.2.6, and the measures for the Credit Status are in Table 6.2.7.
| Table 6.2.5 Uncetainty measures for the distribution of (Purchase, Non-purchase) of entire data | ||||
|---|---|---|---|---|
| Purchasing group \(G_1\) |
Non-purchasing group \(G_2\) |
Total | Uncetainty measures | |
Entire data |
8 |
12 |
20 |
$$ \small \begin{align} \text{Entropy coefficient} &= - 0.4 \times log_{2} 0.4 - (1-0.4) \times log_{2} (1-0.4) = 0.9710 \\ \text{Gini coefficient} &= 1 - {0.4}^2 - (1-0.4)^2 = 0.4800\\ \text{Classification error rate} &= 1 - max\{0.4 , 1-0.4 \} = 0.4000 \end{align} $$ |
| Table 6.2.6 Uncetainty measures for the distribution of (Purchase, Non-purchase) of Gender | ||||
|---|---|---|---|---|
| Gender | Purchasing group \(G_1\) |
Non-purchasing group \(G_2\) |
Total | Uncetainty measures |
Male |
4 |
6 |
10 |
$$ \small \begin{align} \text{Entropy coefficient} &= - 0.4 \times log_{2} 0.4 - (1-0.4) \times log_{2} (1-0.4) = 0.9710 \\ \text{Gini coefficient} &= 1 - {0.4}^2 - (1-0.4)^2 = 0.4800\\ \text{Classification error rate} &= 1 - max\{0.4 , 1-0.4 \} = 0.4000 \end{align} $$ |
Female |
4 |
6 |
10 |
$$ \small \begin{align} \text{Entropy coefficient} &= - 0.4 \times log_{2} 0.4 - (1-0.4) \times log_{2} (1-0.4) = 0.9710 \\ \text{Gini coefficient} &= 1 - {0.4}^2 - (1-0.4)^2 = 0.4800\\ \text{Classification error rate} &= 1 - max\{0.4 , 1-0.4 \} = 0.4000 \end{align} $$ |
| Table 6.2.7 Uncetainty measures for the distribution of (Purchase, Non-purchase) of Credit Status data | ||||
|---|---|---|---|---|
| Credit Status | Purchasing group \(G_1\) |
Non-purchasing group \(G_2\) |
Total | Uncetainty measures |
Good |
7 |
3 |
10 |
$$ \begin{align} \text{Entropy coefficient} &= - 0.7 \times log_{2} 0.7 - (1-0.7) \times log_{2} (1-0.7) = 0.8813 \\ \text{Gini coefficient} &= 1 - {0.7}^2 - (1-0.7)^2 = 0.4200\\ \text{Classification error rate} &= 1 - max\{0.7 , 1-0.7 \} = 0.3000 \end{align} $$ |
Bad |
1 |
9 |
10 |
$$ \begin{align} \text{Entropy coefficient} &= - 0.1 \times log_{2} 0.1 - (1-0.1) \times log_{2} (1-0.1) = 0.4690 \\ \text{Gini coefficient} &= 1 - {0.1}^2 - (1-0.1)^2 = 0.1800\\ \text{Classification error rate} &= 1 - max\{0.1 , 1-0.1 \} = 0.1000 \end{align} $$ |
When looking at the uncertainty for the two variables, each attribute of Credit Status is relatively less than the Gender attribute, so branching using Credit Status is reasonable.
| Table 6.2.8 \(a \times k\) frequency table and uncetainty measure of the variable \(A\) | ||||||
|---|---|---|---|---|---|---|
| Variable \(A\) | Group \(G_1\) | Group \(G_2\) | \(\cdots\) | Group \(G_k\) | Total | Uncetainty |
| \(A_1\) | \(O_{11}\) | \(O_{12}\) | \(\cdots\) | \(O_{1k}\) | \(O_{1 \cdot} \) | \(I(A_1)\) |
| \(A_2\) | \(O_{21}\) | \(O_{22}\) | \(\cdots\) | \(O_{2k}\) | \(O_{2 \cdot }\) | \(I(A_2)\) |
| \(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) |
| \(A_a\) | \(O_{a1}\) | \(O_{a2}\) | \(\cdots\) | \(O_{ak}\) | \(O_{a \cdot} \) | \(I(A_a)\) |
| Total | \(O_{\cdot 1}\) | \(O_{\cdot 2}\) | \(\cdots\) | \(O_{\cdot k}\) | \(O_{\cdot \cdot }\) | Uncertainty of \(A\) \(I(A\)) |
The uncertainty of the variable \(A\) is the expected value of each attribute \(A_{i}\) by weighting the proportion of the observed frequency, \(\frac{O_{i \cdot}}{O_{\cdot \cdot}}\), as follows; $$ I(A) = \frac{O_{1 \cdot}}{O_{\cdot \cdot}} \times I(A_{1}) + \frac{O_{2 \cdot}}{O_{\cdot \cdot}} \times I(A_{2}) + \cdots + \frac{O_{a \cdot}}{O_{\cdot \cdot}} \times I(A_{a}) $$ If we do not know the information of the variable \(A\), the uncertainty of this node \(T\), \(I(T)\), is the uncertainty about the distribution of each group proportion. In the case of the entropy coefficient, it is as follows; $$ I(T) = - \sum_{j=1}^{k} \left( \frac{O_{\cdot j}}{O_{\cdot \cdot}} \right) \;\; log_{2} \left( \frac{O_{\cdot j}}{O_{\cdot \cdot}} \right) $$ In the decision tree, a variable for branching is selected if it has a large difference between the uncertainty of the current node, \(I(T)\), and the expected uncertainty of a variable \(A\), \(I(A)\). This difference is called an information gain and is expressed as \(\Delta\). The information gain at the current node \(T\) by branching into the variable \(A\) is as follows; $$ \Delta = I(T) - I(A) $$ The greater information gain of one variable implies that by branching into this variable, more uncertainty is removed, and, therefore, more accurate classification is expected. The information gain obtained using the entropy coefficient or Gini coefficient tends to prefer a variable with many variable values. In order to overcome this problem, the information gain ratio, which is the information gain divided by the uncertainty of the current node \(T\) is often used as the basis for branching. $$ \text{Information gain ratio} = \frac{\Delta}{I(T)} $$
Answer
Using the uncertainty values for each measure calculated in Example 6.2.3, the information gain for each measure of the Gender variable is as follows; $$ \small \begin{align} \text{Information gain by entropy} &= 0.9710 - \left( \frac{10}{20} \times 0.9710 + \frac{10}{20} \times 0.9710 \right) = 0.0000 \\ \text{Information gain by Gini} &= 0.4800 - \left( \frac{10}{20} \times 0.4800 + \frac{10}{20} \times 0.4800 \right) = 0.0000 \\ \text{Information gain by misclassification error} &= 0.4000 - \left( \frac{10}{20} \times 0.4000 + \frac{10}{20} \times 0.4000 \right) = 0.0000 \\ \end{align} $$ That is, since the Gender variable has the same uncertainty as the current node, there is no information gain for classification that can be obtained by branching. The information gain for the Credit Status variable is as follows; $$ \small \begin{align} \text{Information gain by entropy} &= 0.9710 - \left( \frac{10}{20} \times 0.8813 + \frac{10}{20} \times 0.4690 \right) = 0.2958 \\ \text{Information gain by Gini} &= 0.4800 - \left( \frac{10}{20} \times 0.4200 + \frac{10}{20} \times 0.1800 \right) = 0.1800 \\ \text{Information gain by misclassification error} &= 0.4000 - \left( \frac{10}{20} \times 0.3000 + \frac{10}{20} \times 0.1000 \right) = 0.2000 \\ \end{align} $$ Therefore, regardless of which measure is used, the Credit Status variable has more information gain than Gender, so it can be said that the Credit Status variable is better for branching at the current node.
Let's take a closer look at the algorithm for creating a decision tree using the following example.
| Table 6.2.9 Survey of customers on gender, age, income, credit status and purchase status | |||||
|---|---|---|---|---|---|
| Number | Gender | Age | Income (unit 10,000 won) |
Credit | Purchase |
| 1 | Male | 20s | LT2000 | Fair | Yes |
| 2 | Female | 30s | GE2000 | Good | No |
| 3 | Female | 20s | GE2000 | Fair | No |
| 4 | Female | 20s | GE2000 | Fair | Yes |
| 5 | Female | 20s | LT2000 | Bad | No |
| 6 | Female | 30s | GE2000 | Fair | No |
| 7 | Female | 30s | GE2000 | Good | Yes |
| 8 | Male | 20s | LT2000 | Fair | No |
| 9 | Female | 20s | GE2000 | Good | No |
| 10 | Male | 30s | GE2000 | Fair | Yes |
| 11 | Female | 30s | GE2000 | Good | Yes |
| 12 | Female | 20s | LT2000 | Fair | No |
| 13 | Male | 30s | GE2000 | Fair | No |
| 14 | Male | 30s | LT2000 | Fair | Yes |
| 15 | Female | 30s | GE2000 | Good | Yes |
| 16 | Female | 30s | GE2000 | Fair | No |
| 17 | Female | 20s | GE2000 | Bad | No |
| 18 | Male | 20s | GE2000 | Bad | No |
| 19 | Male | 30s | GE2000 | Good | Yes |
| 20 | Male | 20s | LT2000 | Fair | No |
Answer
In the decision tree algorithm, the data set \(\small E\) is the data in Table 6.2.9, and the variable set is \(\small F\) = {Gender, Age, Income, Credit}. The target variable, Purchase, has two groups, {Yes, No}. The stopping rule of the decision tree is ‘If the number of data in each leaf is 5 or less, do not divide any more’, and ‘If all are classified into one group, stop with the leaf as the group’.
The number of data in the current data set is 20, so stopping.conditon(\(\small E, F\)) in step 1 is false, so go to step 6. For the root node \(\small T\)'s creatNode(), the entropy coefficient \(\small I(T) \) for the distribution of the purchasing group(\(\small G_1\)) and the non-purchasing group (\(\small G_2\)), (8/20, 12/20), is as follows; $$ \small I(T) = - 0.4 \times log_{2} 0.4 - 0.6 \times log_{2} 0.6 = 0.9710 $$ In order to find the optimal branch split, find_best_split(), of step 7, a cross-table is obtained for each variable by group, and the expected information and information gain for the variable are obtained as in Table 6.2.10 using the entropy coefficient. Since the information gain of the credit status is the largest, the root node becomes the credit status, and the set of variable values of credit status in step 8 becomes \(\small V\) = {Bad, Fair, Good}. The \(\small E_{Bad}, E_{Fair}, E_{Good}\) according to the credit status in step 10 are drawn in the form of a decision tree as in <Figure 6.2.3>.
| Table 6.2.10 Expected information and information gain for each variable | ||||||
|---|---|---|---|---|---|---|
| Variable | Purchasing group \(G_1\) | Non-purchasing group \(G_2\) | Total | Entropy | Information gain \(\Delta\) |
|
| Gender | Female | 4 | 8 | 12 | 0.9183 | |
| Male | 4 | 4 | 8 | 1.0000 | ||
| Expected entropy | 0.9510 | 0.0200 | ||||
| Age | 20s | 2 | 8 | 10 | 0.7219 | |
| 30s | 6 | 4 | 10 | 0.9710 | ||
| Expected entropy | 0.8464 | 0.1246 | ||||
| Income | GE200 | 6 | 8 | 14 | 0.9852 | |
| LT200 | 2 | 4 | 6 | 0.9783 | ||
| Expected entropy | 0.9651 | 0.0059 | ||||
| Credit | Bad | 0 | 3 | 3 | 0.0000 | |
| Fair | 4 | 7 | 11 | 0.9457 | ||
| Good | 4 | 2 | 6 | 0.9183 | ||
| Expected entropy | 0.9756 | 0.1754 | ||||
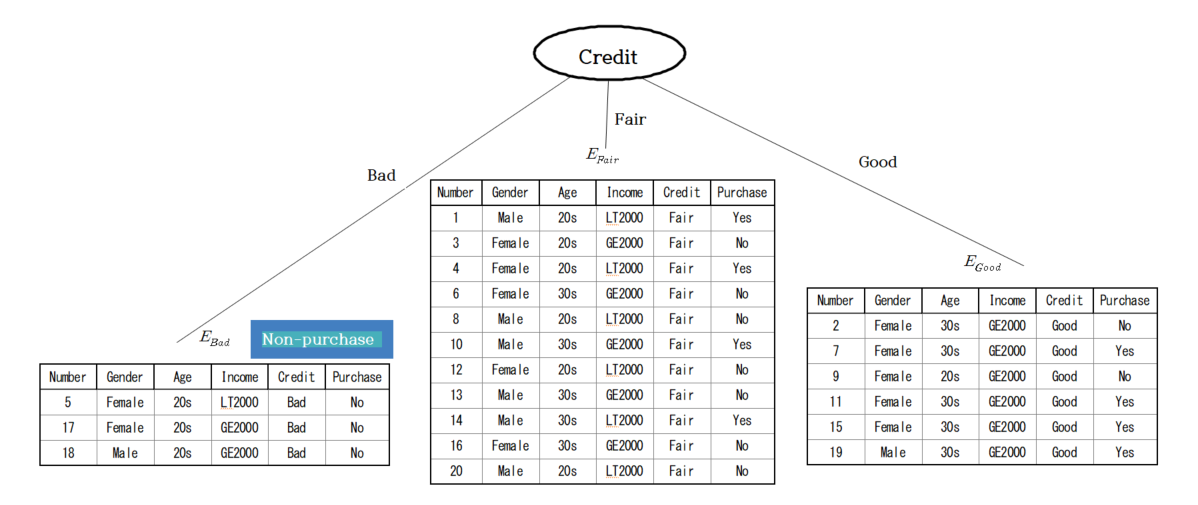
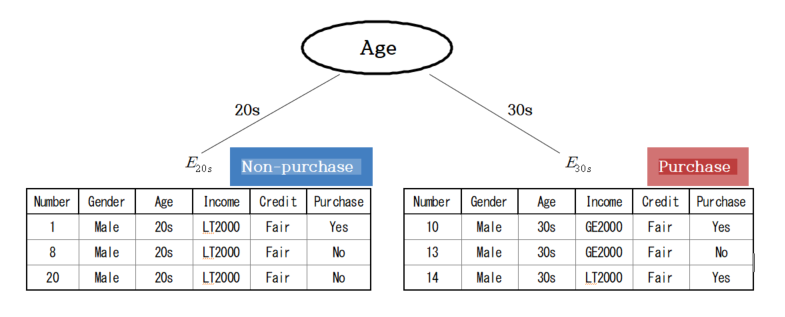
The TreeGrowth() algorithm is repeatedly applied to each data set until the stopping rule is satisfied (step 11). Among these, the data sets of 3 people with Bad credit, \(\small E_{Bad} \), are all Non-purchasing groups, satisfying the stopping rule, so they are not branching any further, and the leaves are marked as the Non-purchasing group.
Since the stopping rule is not satisfied for the data set of 11 people with Fair credit, \(\small E_{Fair} \), this data set needs further split. The entropy coefficients for the distribution (4/11, 7/11) of the Purchasing group (\(\small G_1 \)) and the Non-purchasing group (\(\small G_2 \)) are as follows. $$ \small I(E_{Fair}) = - \frac{4}{11} \times log_{2} \frac{4}{11} - \frac{7}{11} \times log_{2} \frac{7}{11} = 0.9457 $$ In order to find the optimal split, find_best_split(), for the 11 people, a cross-table for each variable by the group is obtained, and the expected information and information gain for the variables are obtained using the entropy coefficient, as shown in Table 6.2.11. In the case of the data set with Fair credit, the information gain for Gender is the largest, so it becomes a node for branching, and a decision tree such as <Figure 6.2.4> is formed.
| Table 6.2.11 Expected information and information gain for each variable in \(\small E_{Fair} \) | ||||||
|---|---|---|---|---|---|---|
| Variable | Purchasing group \(G_1\) | Non-purchasing group \(G_2\) | Total | Entropy | Information gain \(\Delta\) |
|
| Gender | Female | 1 | 4 | 5 | 0.7219 | |
| Male | 3 | 3 | 6 | 1.0000 | ||
| Expected entropy | 0.8736 | 0.0721 | ||||
| Age | 20s | 2 | 4 | 6 | 0.9183 | |
| 30s | 2 | 3 | 5 | 0.9710 | ||
| Expected entropy | 0.9422 | 0.0034 | ||||
| Income | GE200 | 2 | 4 | 6 | 0.9183 | |
| LT200 | 2 | 3 | 5 | 0.9710 | ||
| Expected entropy | 0.9422 | 0.0034 | ||||
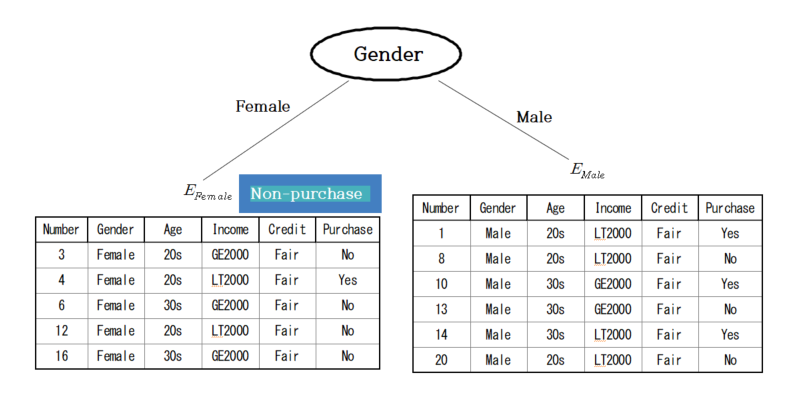
As shown in the Figure 6.2.4, there are 5 data sets of Female with Fair credit, \(\small E_{Female} \), which satisfies the stopping rule, so they are not split any further. Since there four people who did not purchase the computer and only one person purchased, this node are marked as Non-purchasing group by majority vote.
As shown in Figure 6.2.4, there are 6 data sets of Male with Fair credit, \(\small E_{Male} \), the stopping rule is not satisfied and this data set needs further split. The entropy coefficients for the distribution (3/6, 3/6) of the Purchasing group (\(\small G_1 \)) and the Non-purchasing group (\(\small G_2 \)) are as follows. $$ \small I(E_{Male}) = - \frac{3}{6} \times log_{2} \frac{3}{6} - \frac{3}{6} \times log_{2} \frac{3}{6} = 1 $$ In order to find the optimal branch split, find_best_split(), for the 6 people, a cross-table by the group for each variable is obtained, and the expected information and information gain for the variables are obtained using the entropy coefficient, as shown in Table 6.2.12. In the case of the Male with Fair credit, the information gain for Age is the largest, so it becomes a node for branching, and a decision tree such as <Figure 6.2.5> is formed. Here, since there are 3 people in their 20s and 30s, there is no more branching, and the 20s becomes the Non-purchasing group, and the 30s becomes the Purchasing group by majority vote.
| Table 6.2.12 Expected information and information gain for each variable in \(\small E_{Male} \) | ||||||
|---|---|---|---|---|---|---|
| Variable | Purchasing group \(G_1\) | Non-purchasing group \(G_2\) | Total | Entropy | Information gain \(\Delta\) |
|
| Age | 20s | 1 | 2 | 3 | 0.9183 | |
| 30s | 2 | 1 | 3 | 0.9183 | ||
| Expected entropy | 0.9183 | 0.0817 | ||||
| Income | GE200 | 1 | 1 | 2 | 1.0000 | |
| LT200 | 2 | 2 | 4 | 1.0000 | ||
| Expected entropy | 1.0000 | 0.0000 | ||||
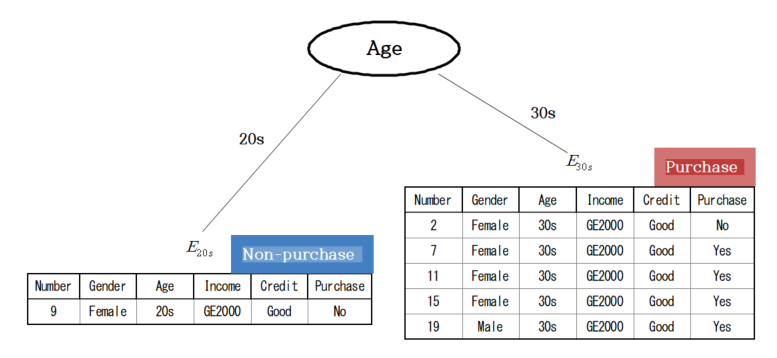
At the root node with Credit, since the stopping rule is not satisfied for the data set of 6 people with Good credit, \(\small E_{Good} \), the entropy coefficients for the distribution (4/6, 2/6) of the Purchasing group (\(\small G_1 \)) and the Non-purchasing group (\(\small G_2 \)) are as follows. $$ \small I(E_{Good}) = - \frac{4}{6} \times log_{2} \frac{4}{6} - \frac{2}{6} \times log_{2} \frac{2}{6} = 0.9183 $$ In order to find the optimal branch split, find_best_split(), for the 6 people, a cross-table by the group for each variable is obtained, and the expected information and information gain for the variables are obtained using the entropy coefficient as shown in Table 6.2.13. Since the information gain of Age is the largest in the data set of Good credit, it becomes a node for branching and forms a decision tree as in <Figure 6.2.6>. As shown in the figure, among the people with Good credit, there is only one person in Age 20s who did not purchase a computer, so it becomes the Non-purchasing group by the stopping rule. There are 5 people in Age 30s, and 4 of them purchased a computer, so they become the Purchasing group by majority vote.
| Table 6.2.13 Expected information and information gain for each variable in \(\small E_{Good} \) | ||||||
|---|---|---|---|---|---|---|
| Variable | Purchasing group \(G_1\) | Non-purchasing group \(G_2\) | Total | Entropy | Information gain \(\Delta\) |
|
| Gender | Female | 3 | 2 | 5 | 0.9710 | |
| Male | 1 | 0 | 1 | 0.0000 | ||
| Expected entropy | 0.8091 | 0.1092 | ||||
| Age | 20s | 0 | 1 | 1 | 0.0000 | |
| 30s | 4 | 1 | 5 | 0.7219 | ||
| Expected entropy | 0.6016 | 0.3167 | ||||
| Income | GE200 | 4 | 2 | 6 | 0.9183 | |
| LT200 | 0 | 0 | 0 | 0.0000 | ||
| Expected entropy | 0.9183 | 0.0000 | ||||
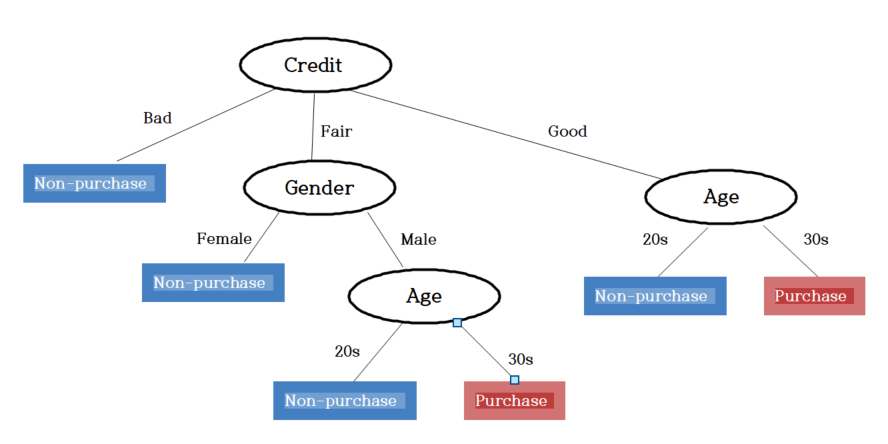
If we combine the above, the decision tree in Figure 6.2.7 is completed. Therefore, the customer who is a 33-year-old man, has a monthly income of 220, and has a good credit is classified as a Purchasing group.
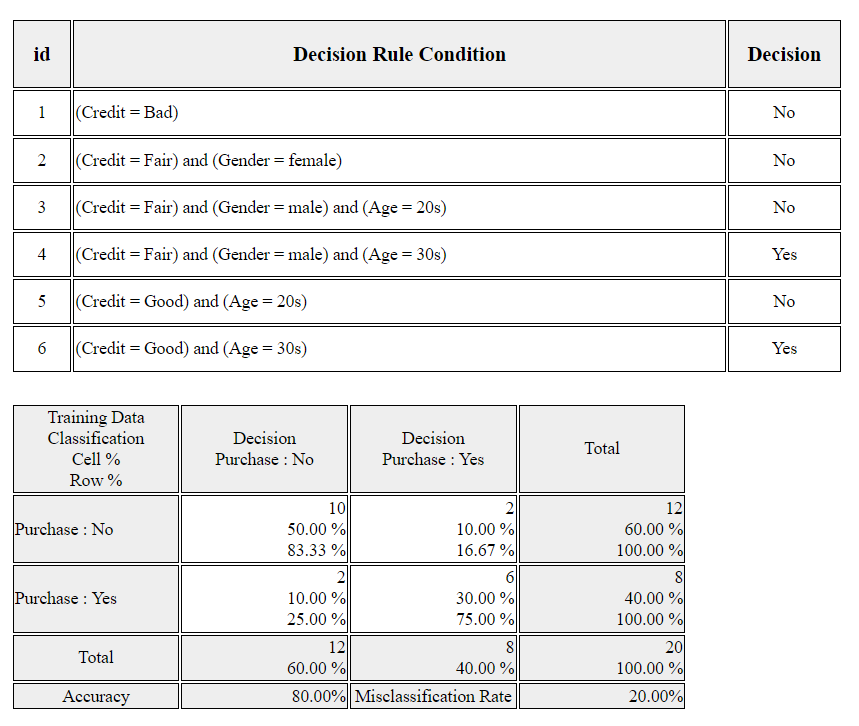
In 『eStatU』 menu, select [Decision Tree] to see the window as follows; Check the criteria for variable selection which is 'Entropy' in this example, enter the maximum tree depth 5 and the minimum number of data 5 for a decision. You can divide the original data set into 'Train' and 'Test' by assigning the percents. Click [Execute] button to see the bar graph matrix and decision tree. Click [Classification Stat] to see the decision rules of this decision tree and the accuracy/misclassification of the classification as in <Figure 6.2.8>. Click [Classification Table] to see the original data and classification result as in <Figure 6.2.9>.
[Decision Tree]
6.2.3 Categorization of a continuous variable
| Table 6.2.14 Survey of customers on income and purchase status | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Purchase | N | N | N | Y | Y | Y | N | N | N | N |
| Income | 100 | 120 | 160 | 180 | 186 | 190 | 210 | 250 | 270 | 300 |
Answer
It is reasonable to examine all middle values of two adjacent incomes as the boundary value, and check how their classification result is made. Then select the boundary value with the least ‘uncertainty’ among them. When a boundary value is examined, if incomes on left side of the boundary value are classified as 'N' group and incomes on the right-side of the boundary value are classified as 'Y' group, a crosstable for classification is summarized as in Table 6.2.15. A boundary value which is smaller than the minimum income or larger than the maximum income is excluded because its division is meaningless. For the first middle value 110 between income 100 and 120 in Table 6.2.11, we classify data using the rule as follows; $$ \small \text{If the income ≤ 110, then classify data as 'N' group, else classify data as 'Y' group} $$ The data 100 is classified correctly using this rule as 'N' group, and the remaining nine data are classified 'Y' group, therefore, three (180, 186, 190) out of nine data are classified correctly as 'Y' group, and six (120, 160, 210, 250, 270, 300) out of nine data are classified incorrectly as 'Y' group as the following crosstable;
Using the Gini coefficient as the uncertainty measure, the expected Gini coefficient when the middle value is 110 calculated as follows; $$ \small \frac{1}{10} \times \left\{ 1 - ( \frac{1}{1} )^2 - ( \frac{0}{1} )^2 \right\} \;+\; \frac{9}{10} \times \left\{ 1 - ( \frac{6}{9} )^2 - ( \frac{3}{9} )^2 \right\} = 0.4000 $$ The expected Gini coefficients for all remaining middle values can be calculated in the same way as Table 6.2.15. The boundary value with the least uncertainty is 200.
| Table 6.2.15 Expected Gini coefficient using the middle value of two adjacent incomes | |||||
|---|---|---|---|---|---|
| Actual group | |||||
| Middle value = 110 | \(N\) | \(Y\) | Total | Expected Gini coefficient | |
| Classified group | \(N\) | 1 | 0 | 1 | |
| \(Y\) | 6 | 3 | 9 | ||
| Total | 10 | 0.400 | |||
| Actual group | |||||
| Middle value = 135 | \(N\) | \(Y\) | Total | Expected Gini coefficient | |
| Classified group | \(N\) | 2 | 0 | 2 | |
| \(Y\) | 5 | 3 | 8 | ||
| Total | 10 | 0.375 | |||
| Actual group | |||||
| Middle value = 170 | \(N\) | \(Y\) | Total | Expected Gini coefficient | |
| Classified group | \(N\) | 3 | 0 | 3 | |
| \(Y\) | 4 | 3 | 7 | ||
| Total | 10 | 0.343 | |||
| Actual group | |||||
| Middle value = 183 | \(N\) | \(Y\) | Total | Expected Gini coefficient | |
| Classified group | \(N\) | 3 | 1 | 4 | |
| \(Y\) | 4 | 2 | 6 | ||
| Total | 10 | 0.417 | |||
| Actual group | |||||
| Middle value = 188 | \(N\) | \(Y\) | Total | Expected Gini coefficient | |
| Classified group | \(N\) | 3 | 2 | 5 | |
| \(Y\) | 4 | 1 | 5 | ||
| Total | 10 | 0.400 | |||
| Actual group | |||||
| Middle value = 200 | \(N\) | \(Y\) | Total | Expected Gini coefficient | |
| Classified group | \(N\) | 3 | 3 | 6 | |
| \(Y\) | 4 | 0 | 4 | ||
| Total | 10 | 0.300 | |||
| Actual group | |||||
| Middle value = 230 | \(N\) | \(Y\) | Total | Expected Gini coefficient | |
| Classified group | \(N\) | 4 | 3 | 7 | |
| \(Y\) | 3 | 0 | 3 | ||
| Total | 10 | 0.343 | |||
| Actual group | |||||
| Middle value = 260 | \(N\) | \(Y\) | Total | Expected Gini coefficient | |
| Classified group | \(N\) | 5 | 3 | 8 | |
| \(Y\) | 2 | 0 | 2 | ||
| Total | 10 | 0.375 | |||
| Actual group | |||||
| Middle value = 285 | \(N\) | \(Y\) | Total | Expected Gini coefficient | |
| Classified group | \(N\) | 6 | 3 | 9 | |
| \(Y\) | 1 | 0 | 1 | ||
| Total | 10 | 0.400 | |||
| Table 6.2.16 crosstable of two interval divisions by purchase status | |||
|---|---|---|---|
| Purchase status | |||
| Age interval 1 | Purchasing group | Non-purchasing group | Total |
| < 25 | 1 | 5 | 6 |
| \(\ge\) 25 | 6 | 8 | 14 |
| Total | 7 | 13 | 20 |
| Age interval 2 | Purchasing group | Non-purchasing group | Total |
| < 35 | 3 | 12 | 15 |
| \(\ge\) 35 | 4 | 1 | 5 |
| Total | 7 | 13 | 20 |
Answer
Let us compare the two crosstables to see which interval division is better. (Age interval 1) has many Non-purchasing groups in both '< 25' and '\(\ge 25\) intervals. (Age unterval 2) has 12 customers in Non-purchasing group out of 15 customers who are '< 35' which is a high proportion, and 4 customers in Purchasing group out of 5 customers who are '\(\ge 35\) which is also a high proportion. Therefore, among the two interval division methods, (Age interval 2) provides more information on purchase. Let us confirm this using the entropy measure.
The expected entropy for the total distribution (\( \frac{7}{20} , \frac{13}{20}\)) of Purchasing group and Non-purchasing group is calculated as follows. $$ \small - (\frac{7}{20}) \; log_{2} ( \frac{7}{20} ) \; - \;(\frac{13}{20} ) \; log_{2} (\frac{13}{20} ) \;=\; 0.9341 $$ The expected entropy and information gain for the two interval divisions are calculated as in Table 6.2.17.
| Table 6.2.17 Expected entropy and information gain of two interval divisions | |||||
|---|---|---|---|---|---|
| Purchase status | |||||
| Age interval 1 | Purchasing group | Non-purchasing group | Total | Entropy | |
| < 25 | 1 | 5 | 6 | \(\small - (\frac{1}{6}) log_{2} ( \frac{1}{6} )^2 - (\frac{5}{6} ) log_{2} (\frac{5}{6} ) = 0.6500\) | |
| \(\ge\) 25 | 6 | 8 | 14 | \(\small - (\frac{6}{14}) log_{2} ( \frac{6}{14} )^2 - (\frac{8}{14} ) log_{2} (\frac{8}{14} ) = 0.9852\) | |
| Total | 7 | 13 | 20 | Expected entropy = \(\small \frac{6}{20} \times 0.6500 + \frac{14}{20} \times 0.9852\) = 0.8847 |
Information gain = \(\small 0.9341 - 0.8847\) = 0.0494 |
| Age interval 2 | Purchasing group | Non-purchasing group | Total | Entropy | |
| < 35 | 3 | 12 | 15 | \(\small - (\frac{3}{15}) log_{2} ( \frac{3}{15} )^2 - (\frac{12}{15} ) log_{2} (\frac{12}{15} ) = 0.7219\) | |
| \(\ge\) 35 | 4 | 1 | 5 | \(\small - (\frac{4}{5}) log_{2} ( \frac{4}{5} )^2 - (\frac{1}{5} ) log_{2} (\frac{1}{5} ) = 0.7219\) | |
| Total | 7 | 13 | 20 | Expected entropy = \(\small \frac{15}{20} \times 0.7219 + \frac{5}{20} \times 0.7219\) = 0.7219 |
Information gain = \(\small 0.9341 - 0.7219\) = 0.2121 |
(Age interval 2) that divides into '< 35' and '\(\ge\) 35' has a large information gain, so this interval division is selected.
6.2.4 Overfitting and pruning decision tree
Post-pruning is a method of removing branches from a completed tree. For example, when pruning subtrees for each node, the expected error rate is calculated, and if this value is the maximum expected error rate, the subtrees are maintained. Otherwise, they are pruned. Pre-pruning and post-pruning are sometimes used in combination.
Characteristics of decision tree model
6.2.5 R and Python practice
R practice
[Colab]
File > Change Directory > C: > Rwork
If you read the data file in R, it looks like as follows.
| # read the data file |
| card <- read.csv("http://estat.me/estat/Example/DataScience/PurchaseByCredit20.csv", header=T, as.is=FALSE) |
card
id Gender Age Income Credit Purchase
1 1 male 20s LT2000 Fair Yes
2 2 female 30s GE2000 Good No
3 3 female 20s GE2000 Fair No
4 4 female 20s GE2000 Fair Yes
5 5 female 20s LT2000 Bad No
6 6 female 30s GE2000 Fair No
7 7 female 30s GE2000 Good Yes
8 8 male 20s LT2000 Fair No
9 9 female 20s GE2000 Good No
10 10 male 30s GE2000 Fair Yes
11 11 female 30s GE2000 Good Yes
12 12 female 20s LT2000 Fair No
13 13 male 30s GE2000 Fair No
14 14 male 30s LT2000 Fair Yes
15 15 female 30s GE2000 Good Yes
16 16 female 30s GE2000 Fair No
17 17 female 20s GE2000 Bad No
18 18 male 20s GE2000 Bad No
19 19 male 30s GE2000 Good Yes
20 20 male 20s LT2000 Fair No
|
| attach(card) |
| Fit a Recursive Partitioning and Regression Trees |
|
|---|---|
| rpart(formula, data, weights, subset, na.action = na.rpart, method, model = FALSE, x = FALSE, y = TRUE, parms, control, cost, ...) | |
| formula | a formula, with a response but no interaction terms. If this a a data frame, that is taken as the model frame (see model.frame). |
| data | an optional data frame in which to interpret the variables named in the formula. |
| method | one of "anova", "poisson", "class" or "exp". If method is missing then the routine tries to make an intelligent guess. If y is a survival object, then method = "exp" is assumed, if y has 2 columns then method = "poisson" is assumed, if y is a factor then method = "class" is assumed, otherwise method = "anova" is assumed. It is wisest to specify the method directly, especially as more criteria may added to the function in future. |
| parms | optional parameters for the splitting function. Anova splitting has no parameters. Poisson splitting has a single parameter, the coefficient of variation of the prior distribution on the rates. The default value is 1. Exponential splitting has the same parameter as Poisson. For classification splitting, the list can contain any of: the vector of prior probabilities (component prior), the loss matrix (component loss) or the splitting index (component split). The priors must be positive and sum to 1. The loss matrix must have zeros on the diagonal and positive off-diagonal elements. The splitting index can be gini or information. The default priors are proportional to the data counts, the losses default to 1, and the split defaults to gini. |
| control | a list of options that control details of the rpart algorithm. See rpart.control. |
| rpart.control(minsplit = 20, minbucket = round(minsplit/3), cp = 0.01, maxcompete = 4, maxsurrogate = 5, usesurrogate = 2, xval = 10, surrogatestyle = 0, maxdepth = 30, ...) | |
| minsplit | the minimum number of observations that must exist in a node in order for a split to be attempted. |
| minbucket | the minimum number of observations in any terminal |
| cp | complexity parameter. Any split that does not decrease the overall lack of fit by a factor of cp is not attempted. For instance, with anova splitting, this means that the overall R-squared must increase by cp at each step. The main role of this parameter is to save computing time by pruning off splits that are obviously not worthwhile. Essentially,the user informs the program that any split which does not improve the fit by cp will likely be pruned off by cross-validation, and that hence the program need not pursue it. |
| maxdepth | Set the maximum depth of any node of the final tree, with the root node counted as depth 0. Values greater than 30 rpart will give nonsense results on 32-bit machines. |
An example of R commands for a decision tree using the dataset card is as follows. The results of practicing a decision tree in R with purchase as the dependent variable of card data and other variables as independent variables are as follows. In Example 6.2.5, the information gain of credit status was the largest, so this variable was the root node. However, since some of the number of data belonging to credit status variable value was small (‘bad’ = 3, ‘good’ = 6, ), the next largest information gain, which is age, was selected as the root node in R.
| install.packages('rpart') |
| library(rpart) |
| fit <- rpart(Purchase ~ Gender + Age + Income + Credit, data = card) |
fit
n= 20
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 20 8 No (0.6000000 0.4000000)
2) Age=20s 10 2 No (0.8000000 0.2000000) *
3) Age=30s 10 4 Yes (0.4000000 0.6000000)
|
However, the analysis result is simple because the minimum number of pruning data of the rpart function is 20 or more by default. Let's change this default setting and prune it. The results of practicing decision trees in R with purchase as the dependent variable of card data and other variables as independent variables are as follows.
| fit2 <- rpart(Purchase ~ Gender + Age + Income + Credit, data = card, control = rpart.control(minsplit = 6)) |
fit2
n= 20
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 20 8 No (0.6000000 0.4000000)
2) Age=20s 10 2 No (0.8000000 0.2000000) *
3) Age=30s 10 4 Yes (0.4000000 0.6000000)
6) Credit=Fair 5 2 No (0.6000000 0.4000000) *
7) Credit=Good 5 1 Yes (0.2000000 0.8000000) *
|
| plot(fit2,compress=T,uniform=T,margin=0.1) |
text(fit2,use.n=T,col='blue')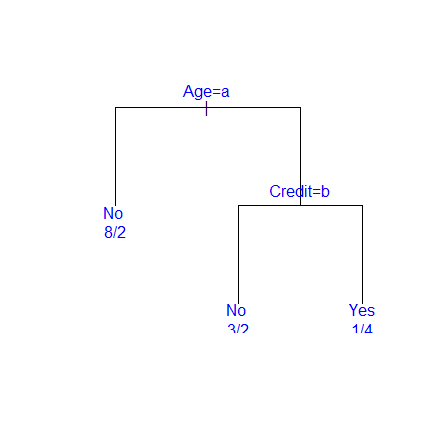
<Figure 6.2.12> Decision tree using R
|
Python practice
[Colab]
|
# Import required libraries import pandas as pd import matplotlib.pyplot as plt # Read the data file url = 'https://raw.githubusercontent.com/ogut77/DataScience/refs/heads/main/PurchaseByCredit40.csv' card = pd.read_csv(url) # Display the data print(card)
id Gender Age Income Credit Purchase
0 1 male 20s LT2000 Fair Yes
1 2 female 30s GE2000 Good No
2 3 female 20s GE2000 Fair No
3 4 female 20s GE2000 Fair Yes
4 5 female 20s LT2000 Bad No
5 6 female 30s GE2000 Fair No
6 7 female 30s GE2000 Good Yes
7 8 male 20s LT2000 Fair No
8 9 female 20s GE2000 Good No
9 10 male 30s GE2000 Fair Yes
10 11 female 30s GE2000 Good Yes
11 12 female 20s LT2000 Fair No
12 13 male 30s GE2000 Fair No
13 14 male 30s LT2000 Fair Yes
14 15 female 30s GE2000 Good Yes
15 16 female 30s GE2000 Fair No
16 17 female 20s GE2000 Bad No
17 18 male 20s GE2000 Bad No
18 19 male 30s GE2000 Good Yes
19 20 male 20s LT2000 Fair No
20 21 male 20s LT2000 Fair Yes
21 22 female 30s GE2000 Good No
22 23 female 20s GE2000 Fair No
23 24 female 20s GE2000 Fair Yes
24 25 female 20s LT2000 Bad No
25 26 female 30s GE2000 Fair No
26 27 female 30s GE2000 Good Yes
27 28 male 20s LT2000 Fair No
28 29 female 20s GE2000 Good No
29 30 male 30s GE2000 Fair Yes
30 31 female 30s GE2000 Good Yes
31 32 female 20s LT2000 Fair No
32 33 male 30s GE2000 Fair No
33 34 male 30s LT2000 Fair Yes
34 35 female 30s GE2000 Good Yes
35 36 female 30s GE2000 Fair No
36 37 female 20s GE2000 Bad No
37 38 male 20s GE2000 Bad No
38 39 male 30s GE2000 Good Yes
39 40 male 20s LT2000 Fair No
# Prepare the data y=card['Purchase'] X=card.drop(['Purchase'], axis=1) # X=pd.get_dummies(X,drop_first=True) # Prepare the data for column in X.select_dtypes(include=['object']).columns: X[column] = label_encoder.fit_transform(X[column]) # Create and train the decision tree model dt = DecisionTreeClassifier() fit = dt.fit(X, y) fit DecisionTreeClassifier() In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org. dt = DecisionTreeClassifier(min_samples_split=6, random_state=42) #Added random_state for reproducibility fit2 = dt.fit(X, y) #Fit on the training data fit2 DecisionTreeClassifier(min_samples_split=6, random_state=42) In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org. # prompt: plot(fit2,compress=T,uniform=T,margin=0.1) # text(fit2,use.n=T,col='blue') in python import matplotlib.pyplot as plt from sklearn.tree import plot_tree # Assuming 'fit2' is your trained DecisionTreeClassifier object and X, y are defined as in your previous code plt.figure(figsize=(20,10)) # Adjust figure size as needed plot_tree(fit2, filled=True, feature_names=X.columns, class_names=True, rounded=True) #filled=True is similar to compress=T, rounded=True is similar to uniform=T plt.show() 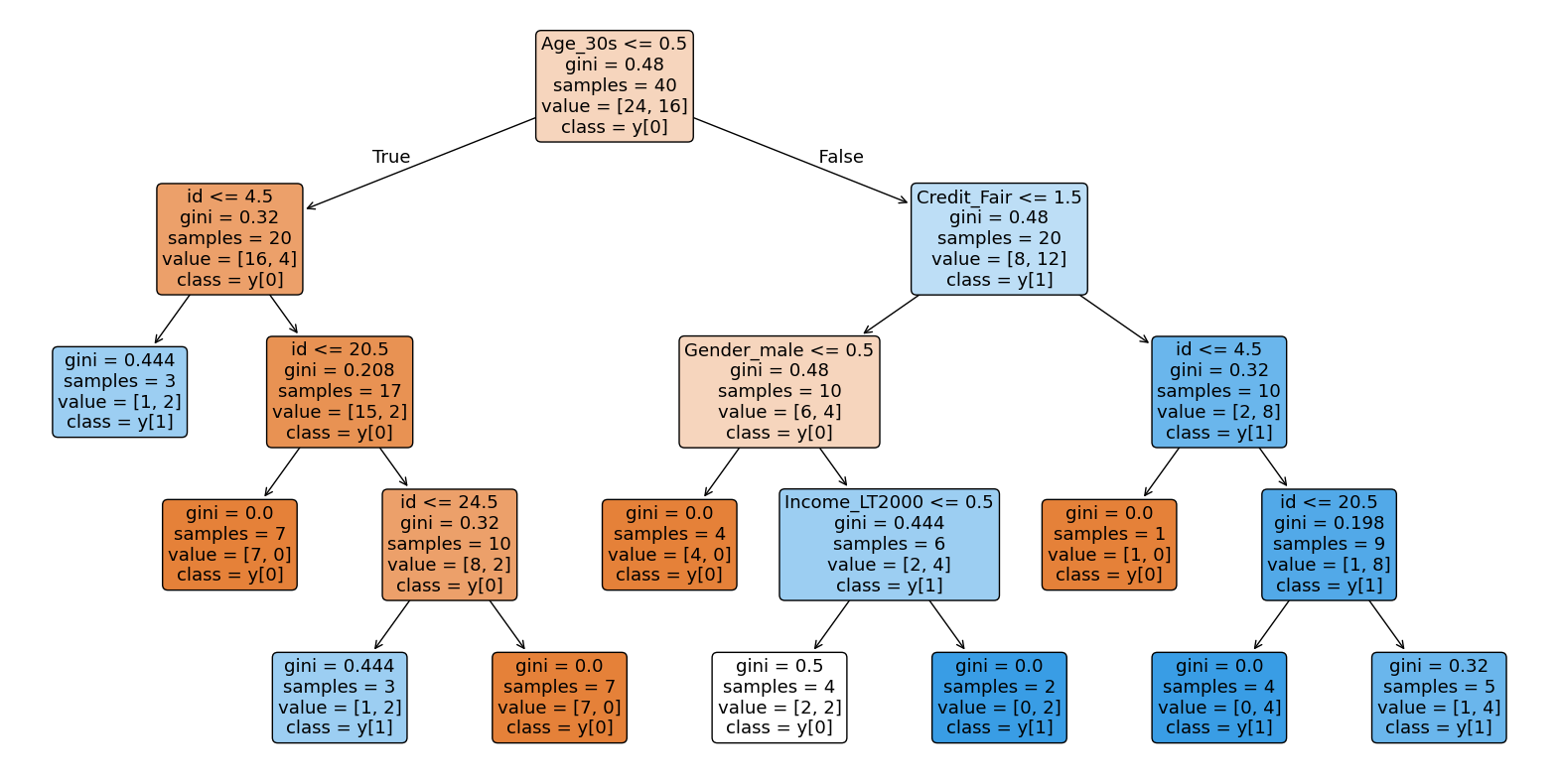
|
6.3 Naive Bayes classification model
6.3.1 Bayes classification
When 20 customers who visited a computer store were surveyed, 8 customers purchased a computer, and 12 customers did not purchase a computer. Based on this information, classify a customer who visited this store on a day whether he would purchase a computer or not.
Answer
Among the 20 customers who visited the store, only 8 (40%) purchased a computer, and 12 (60%) did not purchase a computer. This information, the probability of the purchasing group is 40% and the probability of the non-purchasing group is 60% by surveying past data, are called prior probabilities. If a decision is made based on these prior probabilities, since the probability of the non-purchasing group is higher than the purchasing group, it is reasonable to classify a customer who visited on a day as into the non-purchasing group.
\(\qquad\)‘If \(P(G_{1})\) ≥ \(P(G_{2})\), classify the data into group \(G_{1}\), otherwise classify it into \(G_{2}\)’
In Example 6.3.1, the classification decision was made using simple prior information such as the probability of the purchasing group and the non-purchasing group. One of the additional information that can be obtained is a customer's age. Suppose there are 10 customers in their age 20's among 20 customers and 10 customers in their age 30's. Among the 8 purchasing groups, 2 customers in their age 20's and 6 are in their age 30's. If a customer who visited the store on a day is in his age 20's, classify the customer whether he purchases the computer or not by calculating the posterior probability.
Answer
The customer's age by the purchasing group (\(\small G_{1}\)) and the non-purchasing group (\(\small G_{2}\)) are summarized in the following table.
| Table 6.3.1 crosstable on Age by Purchasing status | |||
|---|---|---|---|
| Age | Purchasing group \(\small G_{1}\) |
Non-purchasing group \(\small G_{2}\) |
Total |
| 20's | 2 | 8 | 10 |
| 30's | 6 | 4 | 10 |
| Total | 8 | 12 | 20 |
Looking at this table, we can see that the purchasing group (\(\small G_{1}\)) has a higher proportion of customers in age 30's, and the non-purchasing group (\(\small G_{2}\)) has a higher proportion of customers in their age 20's. The age distribution of each group is called the likelihood probability distribution. When the age of 20's is represented as \(\small X\), the probability of age 20s in the purchasing group is 2/8, which is denoted as the conditional probability \(\small P( X | G_{1} ) \) and the probability of age 20's in the non-purchasing group is 8/12, which is denoted as \(\small P( X | G_{2} ) \). If a customer who visited on a day was in his age 20's, the probability that this customer would purchase the computer is called the posterior probability of the purchasing group and is denoted as \(\small P( G_{1} | X ) \). This posterior probability can be obtained as follows using Bayes' theorem. $$ \small \begin{align} P( G_{1} | X ) &= \frac {P( G_{1} ) \times P(X|G_{1}) }{P( G_{1} ) \times P(X|G_{1}) + P( G_{2} ) \times P(X|G_{2})} \\ &= \frac{ \frac{8}{20} \times \frac{2}{8} }{ \frac{8}{20} \times \frac{2}{8} + \frac{12}{20} \times \frac{8}{12} } = 0.2 \end{align} $$ Here, the denominator is the probability of all age 20's, \(\small P( X ) \) = 10/20, and the numerator means the proportion of age 20's who purchased the computer, 2/20. In the same way, the posterior probability of non-purchasing goup among age 20's is denoted as \(\small P( G_{2} | X ) \), and is calculated as follows using Bayes' theorem. $$ \small \begin{align} P( G_{2} | X ) &= \frac {P( G_{2} ) \times P(X|G_{2}) }{P( G_{1} ) \times P(X|G_{1}) + P( G_{2} ) \times P(X|G_{2})} \\ &= \frac{ \frac{12}{20} \times \frac{8}{12} }{ \frac{8}{20} \times \frac{2}{8} + \frac{12}{20} \times \frac{8}{12} } = 0.8 \end{align} $$ Therefore, since the posterior probability that a customer in age 20's belongs to the non-purchasing group is 0.8, which is higher than the posterior probability of belonging to the purchasing group of 0.2, this customer is classified as a non-purchasing group. As a result, when we obtain additional information that the visitor is in age 20's, we can see that the probability that this person belongs to the purchasing group of 0.2 is lower than the prior probability of 0.4.
\(\qquad\) ‘If \(\small P( G_{1} | X ) \) ≥ \(\small P( G_{2} | X ) \), classify data as \(\small G_{1}\), otherwise classify as \(\small G_{2}\)’
Here, \(\small P( G_{1} | X ) \) and \(\small P( G_{2} | X ) \) have the same denominator in the calculation of the posterior probability, so the classification rule can be written as follows.
\(\qquad\) ‘If \(\small \frac{P( X | G_{1} )}{P( X | G_{2} )} \) ≥ \(\small \frac{P(G_{2})}{P(G_{1})} \), classify data as \(\small G_{1}\), otherwise classify as \(\small G_{2}\)’
Suppose that prior probabilities of \(k\) number of groups, \(\small G_{1}, G_{2}, ... , G_{k}\), are \(\small P(G_{1}), P(G_{2}), ... , P(G_{k})\), and likelihood probability distribution functions for each group are \(\small P( \boldsymbol X | G_{1}), P( \boldsymbol X | G_{2}), ... , P( \boldsymbol X | G_{k})\). Given the observation data \(\small \boldsymbol x\) for classification, let the posterior probabilities that \(\small \boldsymbol x\) comes from each group be \(\small P(G_{1} | \boldsymbol x), P(G_{2} | \boldsymbol x), ... , P(G_{k} | \boldsymbol x)\). The Bayes classification rule is as follows.
\(\qquad\) 'Classify \(\boldsymbol x\) into a group with the highest posterior probability'
If we denote the likelihood probability functions as \(\small f_{1}(\boldsymbol x), f_{2}(\boldsymbol x), ... , f_{k}(\boldsymbol x)\), since the denominators in the calculation of posterior probabilities are the same, the Bayes classification rule can be written as follows.
\(\qquad\) 'If \(\small P(G_{k}) f_{k}(\boldsymbol x) ≥ P(G_{i}) f_{i}(\boldsymbol x) \) for all \(k\) ≠ \(i\), classify \(\boldsymbol x\) into group \(\small G_{k}\)'
If there are only two groups \(\small G_{1}\)and \(\small G_{2}\), the Bayes classification rule is expressed as follows.
\(\qquad\) 'if \( \frac{f_{1}(\boldsymbol x)}{f_{2}(\boldsymbol x)} ≥ \frac{P(G_{2})}{P(G_{1})} \), classify \(\boldsymbol x\) into group \(\small G_{1}\), else into group \(\small G_{2}\)'
6.3.2 Naive Bayes classification model for categorical data
| Table 6.3.2 Survey of customers on age, income, credit status and purchasing status | |||||
|---|---|---|---|---|---|
| Number | Age | Income (unit USD) |
Credit | Purchase | |
| 1 | 20s | LT2000 | Fair | Yes | |
| 2 | 30s | GE2000 | Good | No | |
| 3 | 20s | GE2000 | Fair | No | |
| 4 | 20s | GE2000 | Fair | Yes | |
| 5 | 20s | LT2000 | Bad | No | |
| 6 | 30s | GE2000 | Fair | No | |
| 7 | 30s | GE2000 | Good | Yes | |
| 8 | 20s | LT2000 | Fair | No | |
| 9 | 20s | GE2000 | Good | No | |
| 10 | 30s | GE2000 | Fair | Yes | |
| 11 | 30s | GE2000 | Good | Yes | |
| 12 | 20s | LT2000 | Fair | No | |
| 13 | 30s | GE2000 | Fair | No | |
| 14 | 30s | LT2000 | Fair | Yes | |
| 15 | 30s | GE2000 | Good | Yes | |
| 16 | 30s | GE2000 | Fair | No | |
| 17 | 20s | GE2000 | Bad | No | |
| 18 | 20s | GE2000 | Bad | No | |
| 19 | 30s | GE2000 | Good | Yes | |
| 20 | 20s | LT2000 | Fair | No | |
If a customer who visited this store one day is 33 years old, has a monthly income of 1900 USD, and has a good credit status, classify him using the posterior probability of whether he will buy a computer or not.
Answer
The one-dimensional likelihood probability distributions, \(\small P(X_{1} | G_{i}),\; P(X_{2} | G_{i}),\; P(X_{3} | G_{i})\), of each variable by purchasing group (\(\small G_{1}\)) and non-purchasing group (\(\small G_{1}\)) are summarized as in Table 6.3.3, and the multidimensional likelihood probability distribution of three variables, \(\small P((X_{1}, X_{2}, X_{3}) | G_{i})\), is summarized as in Table 6.3.4.
| Table 6.3.3 One-dimensional likelihood probability distributions on Age, Income and Credit | |||
|---|---|---|---|
| Age | Purchasing group \(\small G_{1}\) |
Non-purchasing group \(\small G_{2}\) |
Total |
| 20's | 2 | 8 | 10 |
| 30's | 6 | 4 | 10 |
| Total | 8 | 12 | 20 |
| Income | Purchasing group \(\small G_{1}\) |
Non-purchasing group \(\small G_{2}\) |
Total |
| LT2000 | 2 | 4 | 6 |
| GE2000 | 6 | 8 | 14 |
| Total | 8 | 12 | 20 |
| Credit | Purchasing group \(\small G_{1}\) |
Non-purchasing group \(\small G_{2}\) |
Total |
| Bad | 0 | 3 | 3 |
| Fair | 4 | 7 | 11 |
| Good | 4 | 2 | 6 |
| Total | 8 | 12 | 20 |
| Table 6.3.4 Multi-dimensional likelihood probability distributions on Age, Income and Credit | |||||
|---|---|---|---|---|---|
| Age | Income | Credit | Purchasing group \(\small G_{1}\) |
Non-purchasing group \(\small G_{2}\) |
Total |
| 20's | LT2000 | Bad | 1 | 1 | |
| Fair | 1 | 3 | 4 | ||
| Good | |||||
| GE2000 | Bad | 2 | 2 | ||
| Fair | 1 | 1 | 2 | ||
| Good | 1 | 1 | |||
| 30's | LT2000 | Bad | |||
| Fair | 1 | 1 | |||
| Good | |||||
| GE2000 | Bad | ||||
| Fair | 1 | 3 | 4 | ||
| Good | 4 | 1 | 5 | ||
| Total | 8 | 12 | 20 | ||
If a customer who visited the computer store is represented as \( \boldsymbol x\) = (\(\small x_{1}, x_{2}, x_{3}\)) = (30s, LT2000, Fair), the posterior probability that this customer belongs to the purchasing group \(\small G_{1}\) is \(\small P(G_{1} | \boldsymbol x )\) and the posterior probability that this customer belongs to the non-purchasing group \(\small G_{2}\) is \(\small P(G_{2} | \boldsymbol x )\). However, in the multidimensional likelihood distribution for the three variables in Table 6.3.4, the probability of a customer being in their 30s, with an income of LT2000, and with fair credit is \(\small P(G_{1} | \boldsymbol x )\) = 1/8 and \(\small P(G_{2} | \boldsymbol x )\) = 0. If the number of samples is insufficient, it is difficult to correctly estimate the likelihood probability distribution. In this case, if variables, age, income, and credit status, can be assumed to be independent, the one-dimensional likelihood probability distribution of each variable is used approximately to estimate the multidimensional likelihood probability distribution as follows.
\( \qquad \small P(\boldsymbol X = (X_{1}, X_{2}, X_{3})\; |\; G_{i}) ≈ P(X_{1} | G_{i}) \; P(X_{2} | G_{i}) \; P(X_{3} | G_{i}) \)
For this problem, the approximate likelihood of customer \(\boldsymbol x\) = (30s, LT2000, Fair) is as follows.
\( \qquad \small P(\boldsymbol x = (30s, LT2000, Fair) \;|\; G_{1}) ≈ \frac{6}{8} \times \frac{2}{8} \times \frac{4}{8} = 0.0938 \)
\( \qquad \small P(\boldsymbol x = (30s, LT2000, Fair) \;|\; G_{2}) ≈ \frac{4}{12} \times \frac{4}{12} \times \frac{7}{12} = 0.0648 \)
Therefore, the posterior probability for each group is as follows.
\( \qquad \small \begin{align} P( G_{1} | \boldsymbol x ) &= \frac {P( G_{1} ) \times P(\boldsymbol x | G_{1}) }{P( G_{1} ) \times P(\boldsymbol x | G_{1}) + P( G_{2} ) \times P(\boldsymbol x | G_{2})} \\ &= \frac{ 0.4 \times 0.0938 }{ 0.4 \times 0.0938 + 0.6 \times 0.0648 } = 0.4911 \end{align} \)
\( \qquad \small \begin{align} P( G_{2} | \boldsymbol x ) &= \frac {P( G_{2} ) \times P(\boldsymbol x | G_{2}) }{P( G_{1} ) \times P(\boldsymbol x | G_{1}) + P( G_{2} ) \times P(\boldsymbol x | G_{2})} \\ &= \frac{ 0.6 \times 0.0648 }{ 0.4 \times 0.0938 + 0.6 \times 0.0648 } = 0.5089 \end{align} \)
Since the posterior probability of belonging to the non-purchasing group is 0.5089, which is greater than the probability of belonging to the purchasing group, which is 0.4911, the customer is classified as the non-purchasing group. Lift chart, confusion matrix and ROC graph are to evaluate the classification model, and they will be explained in the next section.
[]
To compensate for the problem of assuming that all variables are independent, subsets of variables can be assumed to be independent, and the likelihood probability distribution can be obtained. This classification model is called a Bayes belief network. In this method, it is necessary to first investigate which variables are related to each other and which variables are independent. For more information, please refer to the references.
6.3.3 Stepwise variable selection
If there are many variables in the data, in general, we use variables that can best explain group variables, that is, variables with high discriminatory power between groups. A stepwise variable selection can be helpful in classifying data to increase accuracy. There are two methods to select variables: forward selection and backward elimination. The forward selection of variables is similar to the variable selection in a decision tree, which selects a variable with the highest information gain using the uncertainty measures or chi-square test. After selecting a variable for classification, add another variable with the next highest information gain in the selection step-by-step until finding a set of variables with the highest classification accuracy.
The backward elimination initially includes all variables for classification and selects a variable to remove from the set of all variables, which can improve classification accuracy. Continue removing a variable from the set of variables until there is no improvement in classification accuracy. The chi-square test, which we discussed in section 6.2.2 is often used for this backward selection of variables in naive Bayes classification. A stepwise method also selects variables using the forward selection method while examining whether the variables already selected can be removed. However, it is not easy to verify whether the ‘optimal’ variable selection was made regardless of the method used. For more information, please refer to the references.
Characteristics of Bayes classification model
6.3.4 R and Python practice - Naive Bayes classification
R practice
[Colab]
| Fit naive Bayes model in which predictors are assumed to be independent within each class label. |
|
|---|---|
|
## Default S3 method: naive_bayes(x, y, prior = NULL, laplace = 0, usekernel = FALSE, usepoisson = FALSE, ...) ## S3 method for class 'formula' naive_bayes(formula, data, prior = NULL, laplace = 0, usekernel = FALSE, usepoisson = FALSE, subset, na.action = stats::na.pass, ...) |
|
| x | matrix or dataframe with categorical (character/factor/logical) or metric (numeric) predictors. |
| y | class vector (character/factor/logical) |
| formula | an object of class "formula" (or one that can be coerced to "formula") of the form: class ~ predictors (class has to be a factor/character/logical). |
| data | matrix or dataframe with categorical (character/factor/logical) or metric (numeric) predictors. |
| prior | vector with prior probabilities of the classes. If unspecified, the class proportions for the training set are used. If present, the probabilities should be specified in the order of the factor levels. |
| laplace | value used for Laplace smoothing (additive smoothing). Defaults to 0 (no Laplace smoothing). |
| usekernel | logical; if TRUE, density is used to estimate the class conditional densities of metric predictors. This applies to vectors with class "numeric". For further details on interaction between usekernel and usepoisson parameters please see Note below. |
| usepoisson | logical; if TRUE, Poisson distribution is used to estimate the class conditional PMFs of integer predictors (vectors with class "integer"). |
| subset | an optional vector specifying a subset of observations to be used in the fitting process. |
| na.actioncp | a function which indicates what should happen when the data contain NAs. By default (na.pass), missing values are not removed from the data and are then omited while constructing tables. Alternatively, na.omit can be used to exclude rows with at least one missing value before constructing tables. |
An example of R commands for a naive Bayes classification in R with purchase as the dependent variable of card data and other variables as independent variables is as follows.
| install.packages('naivebayes') |
| library(naivebayes) |
| nbfit <- naive_bayes(Purchase ~ Gender + Age + Income + Credit, data = card) |
nbfit
Call: naive_bayes.formula(formula = Purchase ~ Gender + Age + Income + Credit, data = card) -------------------------------------------------------- Laplace smoothing: 0 -------------------------------------------------------- A priori probabilities: No Yes 0.6 0.4 -------------------------------------------------------- Tables: -------------------------------------------------------- :: Gender (Bernoulli) -------------------------------------------------------- Gender No Yes Female 0.6666667 0.5000000 Male 0.3333333 0.5000000 -------------------------------------------------------- :: Age (Bernoulli) -------------------------------------------------------- Age No Yes 20s 0.6666667 0.2500000 30s 0.3333333 0.7500000 -------------------------------------------------------- :: Income (Bernoulli) -------------------------------------------------------- Income No Yes GE2000 0.6666667 0.7500000 LT2000 0.3333333 0.2500000 -------------------------------------------------------- :: Credit (Categorical) -------------------------------------------------------- Credit No Yes Bad 0.2500000 0.0000000 Fair 0.5833333 0.5000000 Good 0.1666667 0.5000000 -------------------------------------------------------- |
| pred <- predict(nbfit, card, type = 'prob')" |
pred
No Yes
[1,] 0.8057554 0.1942446043
[2,] 0.2084691 0.7915309446
[3,] 0.8468809 0.1531190926
[4,] 0.8468809 0.1531190926
[5,] 0.9994378 0.0005621838
[6,] 0.4796574 0.5203426124
[7,] 0.2084691 0.7915309446
[8,] 0.8057554 0.1942446043
[9,] 0.6124402 0.3875598086
[10,] 0.3154930 0.6845070423
[11,] 0.2084691 0.7915309446
[12,] 0.8924303 0.1075697211
[13,] 0.3154930 0.6845070423
[14,] 0.4087591 0.5912408759
[15,] 0.2084691 0.7915309446
[16,] 0.4796574 0.5203426124
[17,] 0.9991570 0.0008430387
[18,] 0.9983153 0.0016846571
[19,] 0.1163636 0.8836363636
[20,] 0.8057554 0.1942446043
|
| pred2 <- predict(nbfit, card) |
pred2
[1] No Yes No No No Yes Yes No No Yes Yes No Yes Yes Yes Yes No No Yes [20] No Levels: No Yes |
| classtable <- table(Purchase, pred2) |
classtable
pred2
Purchase No Yes
No 8 4
Yes 2 6
|
| sum(diag(classtable)) / sum(classtable) [1] 0.7 |
Python practice
[Colab]
|
# Import required libraries import pandas as pd from sklearn.naive_bayes import GaussianNB from sklearn import preprocessing label_encoder = preprocessing.LabelEncoder() # Load the dataset url = 'https://raw.githubusercontent.com/ogut77/DataScience/refs/heads/main/PurchaseByCredit40.csv' card = pd.read_csv(url) # Prepare the data X = card.drop('Purchase', axis=1) y = card['Purchase'] # X = pd.get_dummies(X, drop_first=True) for column in X.select_dtypes(include=['object']).columns: X[column] = label_encoder.fit_transform(X[column]) # Create and train the Naive Bayes model nbfit = GaussianNB() nbfit.fit(X, y) # Now you can use nbfit to make predictions: # predictions = nbfit.predict(X_test) nbfit GaussianNB() In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org. X id Gender Age Income Credit 0 1 1 0 1 1 1 2 0 1 0 2 2 3 0 0 0 1 3 4 0 0 0 1 4 5 0 0 1 0 5 6 0 1 0 1 6 7 0 1 0 2 7 8 1 0 1 1 8 9 0 0 0 2 9 10 1 1 0 1 10 11 0 1 0 2 11 12 0 0 1 1 12 13 1 1 0 1 13 14 1 1 1 1 14 15 0 1 0 2 15 16 0 1 0 1 16 17 0 0 0 0 17 18 1 0 0 0 18 19 1 1 0 2 19 20 1 0 1 1 20 21 1 0 1 1 21 22 0 1 0 2 22 23 0 0 0 1 23 24 0 0 0 1 24 25 0 0 1 0 25 26 0 1 0 1 26 27 0 1 0 2 27 28 1 0 1 1 28 29 0 0 0 2 29 30 1 1 0 1 30 31 0 1 0 2 31 32 0 0 1 1 32 33 1 1 0 1 33 34 1 1 1 1 34 35 0 1 0 2 35 36 0 1 0 1 36 37 0 0 0 0 37 38 1 0 0 0 38 39 1 1 0 2 39 40 1 0 1 1 # prompt: pred <- predict(nbfit, card, type = 'prob') # pred in python # Predict probabilities using the trained Naive Bayes model pred = nbfit.predict_proba(X) # Print or further process the predictions pred
array([[0.84828263, 0.15171737],
[0.16545941, 0.83454059],
[0.86877169, 0.13122831],
[0.86893468, 0.13106532],
[0.99576268, 0.00423732],
[0.45305897, 0.54694103],
[0.16658356, 0.83341644],
[0.84973975, 0.15026025],
[0.61725121, 0.38274879],
[0.2831043 , 0.7168957 ],
[0.16797331, 0.83202669],
[0.9236716 , 0.0763284 ],
[0.28492091, 0.71507909],
[0.41739315, 0.58260685],
[0.16980815, 0.83019185],
[0.46020741, 0.53979259],
[0.99268741, 0.00731259],
[0.98470712, 0.01529288],
[0.08941323, 0.91058677],
[0.85496654, 0.14503346],
[0.85555067, 0.14444933],
[0.17412572, 0.82587428],
[0.87604521, 0.12395479],
[0.87661948, 0.12338052],
[0.99606019, 0.00393981],
[0.47219023, 0.52780977],
[0.1781103 , 0.8218897 ],
[0.86023739, 0.13976261],
[0.63794767, 0.36205233],
[0.30223529, 0.69776471],
[0.18186659, 0.81813341],
[0.93044127, 0.06955873],
[0.30658426, 0.69341574],
[0.44384514, 0.55615486],
[0.18615261, 0.81384739],
[0.48903735, 0.51096265],
[0.99350584, 0.00649416],
[0.98645826, 0.01354174],
[0.10032986, 0.89967014],
[0.87048142, 0.12951858]])
# prompt: pred2 <- predict(nbfit, card) # pred2 in python # Predict probabilities using the trained Naive Bayes model pred2 = nbfit.predict(X) # Print or further process the predictions pred2
array(['No', 'Yes', 'No', 'No', 'No', 'Yes', 'Yes', 'No', 'No', 'Yes',
'Yes', 'No', 'Yes', 'Yes', 'Yes', 'Yes', 'No', 'No', 'Yes', 'No',
'No', 'Yes', 'No', 'No', 'No', 'Yes', 'Yes', 'No', 'No', 'Yes',
'Yes', 'No', 'Yes', 'Yes', 'Yes', 'Yes', 'No', 'No', 'Yes', 'No'],
dtype='U3')
from sklearn.metrics import confusion_matrix import seaborn as sns # Assuming 'y' contains the true labels and 'pred2' contains the predicted labels cm = confusion_matrix(y, pred2) # Plot the confusion matrix using seaborn plt.figure(figsize=(8, 6)) sns.heatmap(cm, annot=True, fmt="d", cmap="Blues") plt.xlabel("Predicted") plt.ylabel("Actual") plt.title("Confusion Matrix") plt.show() 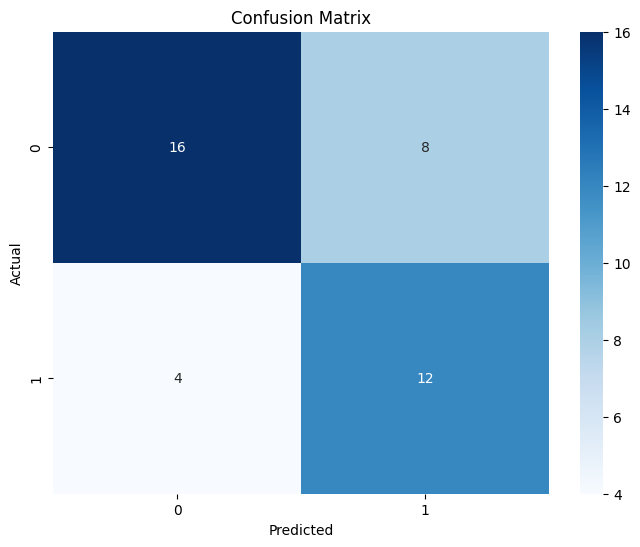
from sklearn.metrics import accuracy_score Accuracy: 0.7 |
6.4 Evaluation and comparison of a classification model
6.4.1 Evaluation of a classification model
| Table 6.4.1 Table for the test results of the actual group and the classified group | ||||
|---|---|---|---|---|
| Classified group | ||||
| \(\small G_1\) | \(\small G_2\) | Total | ||
| Actual group | \(\small G_1\) | \(\small f_{11}\) | \(\small f_{12}\) | \(\small f_{11} + f_{12}\) |
| \(\small G_2\) | \(\small f_{21}\) | \(\small f_{22}\) | \(\small f_{21} + f_{22}\) | |
| Total | \(n\) | |||
Here, \(f_{ij}\) means the number of data of the group \(G_i\) classified into the group \(G_j\). The number of data correctly classified out of the total data is \(f_{11} + f_{22}\), and the number of data incorrectly classified is \(f_{12} + f_{21}\). As we defined in the section 6.1.1, the accuracy of the classification model is the ratio of the number of correctly classified data out of the total number of data, and the error rate is the ratio of the number of incorrectly classified data out of the total number of data. $$ \begin{align} \text{Accuracy} &= \frac{f_{11} + f_{22}}{n} \\ \text{Error rate} &= \frac{f_{12} + f_{21}}{n} \end{align} $$ The accuracy and error rate can be considered reasonable measures if the risk of misclassification of the group \(G_{1}\), \(f_{12}\), and the risk of misclassification of the group \(G_{2}\), \(f_{21}\), are the same. However, in real problems, the risk of misclassification may be different for each group. For example, consider two types of misclassification that a doctor misclassifies a cancer patient as a healthy person and a doctor misclassifies a healthy person as a cancer patient. The former case has a greater risk of misclassification than the latter because it carries the risk of shortening life. When the risk of misclassification is different, the following measures called sensitivity, specificity, and precision are used. $$ \begin{align} \text{Sensitivity} &= \frac{f_{11}}{f_{11} + f_{12}} \\ \text{Specificity} &= \frac{f_{22}}{f_{21} + f_{22}} \\ \text{Precision} &= \frac{f_{11}}{f_{11} + f_{21}} \end{align} $$ In the example above, sensitivity is the rate at which actual cancer patients are classified as cancer patients, specificity is the rate at which healthy people are classified as healthy people, and precision is the rate at which actual cancer patients are classified among classified as cancer patients. Accuracy can be expressed as the weighted sum of sensitivity and specificity. $$ \text{Accuracy} = \frac{f_{11} + f_{12}}{n} \text{(Sensitivity)} + \frac{f_{21} + f_{22}}{n} \text{(Specificity)} $$
Lift chart, confusion matrix, expected profit and ROC curve are graphs that evaluate classification models using sensitivity and specificity.
Lift Chart
| Table 6.4.2 Survey data and classification results with posterior probability of each group | |||||||
|---|---|---|---|---|---|---|---|
| Number | Age | Income (unit USD) |
Credit | Purchase | Classification | Posterior Group 1: No |
Posterior Group 2: Yes |
| 1 | 20s | LT2000 | Fair | Yes | No | 0.862 | 0.138 |
| 2 | 30s | GE2000 | Good | No | Yes | 0.165 | 0.835 |
| 3 | 20s | GE2000 | Fair | No | No | 0.806 | 0.194 |
| 4 | 20s | GE2000 | Fair | Yes | No | 0.806 | 0.194 |
| 5 | 20s | LT2000 | Bad | No | No | 1.000 | 0.000 |
| 6 | 30s | GE2000 | Fair | No | Yes | 0.409 | 0.591 |
| 7 | 30s | GE2000 | Good | Yes | Yes | 0.165 | 0.835 |
| 8 | 20s | LT2000 | Fair | No | No | 0.862 | 0.138 |
| 9 | 20s | GE2000 | Good | No | No | 0.542 | 0.458 |
| 10 | 30s | GE2000 | Fair | Yes | Yes | 0.409 | 0.591 |
| 11 | 30s | GE2000 | Good | Yes | Yes | 0.165 | 0.835 |
| 12 | 20s | LT2000 | Fair | No | No | 0.862 | 0.138 |
| 13 | 30s | GE2000 | Fair | No | Yes | 0.409 | 0.591 |
| 14 | 30s | LT2000 | Fair | Yes | No | 0.509 | 0.491 |
| 15 | 30s | GE2000 | Good | Yes | Yes | 0.165 | 0.835 |
| 16 | 30s | GE2000 | Fair | No | Yes | 0.409 | 0.591 |
| 17 | 20s | GE2000 | Bad | No | No | 1.000 | 0.000 |
| 18 | 20s | GE2000 | Bad | No | No | 1.000 | 0.000 |
| 19 | 30s | GE2000 | Good | Yes | Yes | 0.165 | 0.835 |
| 20 | 20s | LT2000 | Fair | No | No | 0.862 | 0.138 |
Answer
In order to make the lift table, we need first to arrange all data in descending order of the 1st group posterior probability, and then organize them into 10 data categories (2 data each category is 10%). Since there are 12 data in group 1 and 8 data in group 2 out of the total 20 data, the baseline response rate of this data is \(\frac{12}{20}\) which is 60%. In each data category, the number of the 1st group data, the cumulated number of data, and the cumulated number of the 1st group data are counted to calculate the response rate, cumulated response rate, and lift of each category. The captured column is the ratio of the number of the 1st group out of the number of data in each category. The % response and Lift of the 1st category which is the upper 10% of data are calculated as follows. $$ \small \begin{align} \text{upper 10% Response} &= \frac{\text{Number of 1st group classified as group 1 in upper 10%}}{\text{Number of data in upper 10%}} \times 100 \\ \text{upper 10% Lift} &= \frac{\text{upper 10% Response}}{\text{Baseline response}} \times 100 \\ \end{align} $$ Table 6.4.3 is the lift table and, and the lift chart is as in <Figure 6.4.1>.
| Table 6.4.3 Lift table for training data using the data in Table 6.4.2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Category upper % |
Number of data | Number of 1st group | Cumulated num. of data | Cumulated num. of 1st group | Captured | Response | Cumulated response | Lift |
| upper (0,10%] | 2 | 2 | 2 | 2 | 1.0 | 1.00 | 1.00 | 1.67 |
| (10,20%] | 2 | 2 | 4 | 4 | 1.0 | 1.00 | 1.00 | 1.67 |
| (20,30%] | 2 | 1 | 6 | 5 | 0.5 | 0.50 | 0.83 | 0.83 |
| (30,40%] | 2 | 2 | 8 | 7 | 1.0 | 1.00 | 0.88 | 1.67 |
| (40,50%] | 2 | 1 | 10 | 8 | 0.5 | 0.50 | 0.80 | 0.83 |
| (50,60%] | 2 | 1 | 12 | 9 | 0.5 | 0.50 | 0.75 | 0.83 |
| (60,70%] | 2 | 2 | 14 | 11 | 1.0 | 1.00 | 0.79 | 1.67 |
| (70,80%] | 2 | 0 | 16 | 11 | 0.0 | 0.00 | 0.69 | 0.00 |
| (80,90%] | 2 | 1 | 18 | 12 | 0.5 | 0.50 | 0.67 | 0.83 |
| (90,100%] | 2 | 0 | 20 | 12 | 0.0 | 0.00 | 0.60 | 0.00 |
<Figure 6.4.1> is a chart using the lift table in Table 6.4.3. The upper percentile of of the data is on the x-axis, and the response rate, which is the rate of actually group 1 when the data corresponding to the upper percentile category are considered as group 1, is plotted on the y-axis.
Since there is a small number of data in this example, we cannot see a general pattern of response rate. In general, response rates show a decreasing pattern by upper % categories and a response rate becomes below of the baseline response at one upper % category. We can also observe a category which the lift becomes below 1. This upper % category can be used which value of the posterior probability will be the boundary to decide a group. A lift chart is also drawn for both training and test data, which is called a cross-lift chart. If it is a stable classification model, the lift charts of the training and test data should not be significantly different.
Confusion matrix
Answer
Consider a classification table created by dividing the posterior probability value into 0.1 units by the cut-off value. For each cut-off value, data smaller than this value are classified into group 2, and data larger than this value are classified into group 1. Table 6.4.4 is the confusion matrix which shows the correct classification, misclassification, accuracy, sensitivity, and specificity of the entire data for each cut-off value. <Figure 6.4.3> is the confusion matrix graph.
| Table 6.4.4 Confusion matrix | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Number | Posterior probability | Number of data | f11 | f12 | f21 | f22 | Accuracy | Sensitivity | Specificity |
| 1 | 0.00 | 20 | 12 | 0 | 8 | 0 | 0.600 | 1.000 | 0.000 |
| 2 | 0.10 | 20 | 12 | 0 | 8 | 0 | 0.600 | 1.000 | 0.000 |
| 3 | 0.20 | 20 | 11 | 1 | 4 | 4 | 0.750 | 0.917 | 0.500 |
| 4 | 0.30 | 20 | 11 | 1 | 4 | 4 | 0.750 | 0.917 | 0.500 |
| 5 | 0.40 | 20 | 11 | 1 | 4 | 4 | 0.750 | 0.917 | 0.500 |
| 6 | 0.50 | 20 | 8 | 4 | 3 | 5 | 0.650 | 0.667 | 0.625 |
| 7 | 0.60 | 20 | 7 | 5 | 2 | 6 | 0.650 | 0.583 | 0.750 |
| 8 | 0.70 | 20 | 7 | 5 | 2 | 6 | 0.650 | 0.583 | 0.750 |
| 9 | 0.80 | 20 | 7 | 5 | 2 | 6 | 0.650 | 0.583 | 0.750 |
| 10 | 0.90 | 20 | 3 | 9 | 0 | 8 | 0.550 | 0.250 | 1.000 |
| 11 | 1.00 | 20 | 0 | 12 | 0 | 8 | 0.400 | 0.000 | 1.000 |
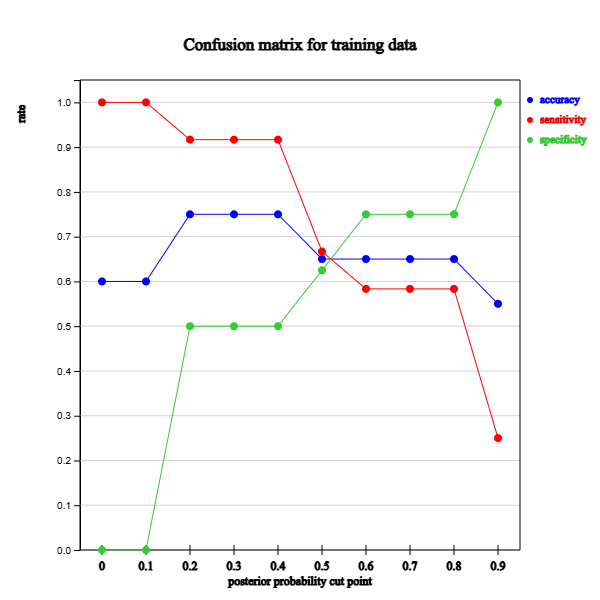
ROC graph
<Figure 6.4.4> is a ROC graph of two classification models, \(\small M_{1}\) and \(\small M_{2}\). In the ROC graph, the point (FPR=0, TPR=0) represents a classification model that classifies all points into group 2, the point (FPR=1, TPR=1) classifies all data into group 1, and the point (FPR=0, TPR=1) represents an ideal model that does not misclassify group 2 data into group 1 and correctly classifies all group 1 data. Therefore, a good classification model should have the classification results located in the upper left corner of the ROC graph. The diagonal line in the figure shows an exceptional model in which both the TPR and FPR ratios are the same, that means a special case in which data are randomly classified into groups 1 and 2 with a fixed probability. In this case, group 1 data is classified into group 1 with probability \(p\) (TPR = \(p\)), and group 2 data is also classified into group 1 with probability \(p\) (FPR = \(p\)). The ROC graph is helpful in comparing the performance of several classification models. In <Figure 6.4.4>, the ROC graph of classification model \(\small M_{1}\) is located upper on the left than that of classification model \(\small M_{2}\). This means that \(\small M_{1}\) has the correct classification rate TPR is always better than the misclassification rate FPR for group 1, so model \(\small M_{1}\) can be said to be better than model \(\small M_{2}\). In this case, one classification model is always better than another classification model, but there are also cases where the ROC graphs of the two models intersect so that neither model can always be said to be better.
The area under the ROC graph is also called the c-statistic, and it can be used to compare how good the performance of the model is on average. In the case of an ideal model (FPR=0, TPR=1), the area is 1, and in the case of a random classification where the classification result of the model is located on the diagonal, the area is \(\frac{1}{2}\). If the area under the ROC graph of one model is larger than that of another model, it can be said to be a better model on average.
To draw a ROC graph, first, sort in ascending order of the posterior probability of group 1 and classify the entire data using each posterior probability value as the cut-off value for classifying the two groups, calculate the sensitivity and specificity, and then draw a connecting line using each sensitivity as the y-axis and (1 - specificity) as the x-axis. If you draw a ROC graph in this way, the area under the curve, c-statistic, can be easily obtained. Let's look at the following example to see how to draw a ROC graph.
Answer
To draw a ROC graph, sort in ascending order of the posterior probability of group 1. First, if we classify all data into group 1, the number of group 1 data classified into group 1 is \(\small f_{11}\) = 12, and the number of group 2 data classified into group 1 is \(\small f_{21}\) = 8. Next, if we classify the first data into group 2 and the second data and above into group 1, we get \(\small f_{11}\) = 11, \(\small f_{12}\) = 1,\(\small f_{21}\) = 8. Next, if we classify the first and second data into group 2 and the third data and above into group 1, we get \(\small f_{11}\) = 11, \(\small f_{12}\) = 1,\(\small f_{21}\) = 7, \(\small f_{22}\) = 1. If we classify in a similar way and obtain TPR and FPR, they are as shown in Table 6.4.5. The rightmost column in the table is the case where all data is classified into group 2. If you draw an ROC graph using the TPR and FPR in this table, it will look like <Figure 6.4.5>.
| Table 6.4.5 Calculation of TPR and FPR for ROC graph | ||||||||
|---|---|---|---|---|---|---|---|---|
| Number | Group | Posterior probability | f11 | f12 | f21 | f22 | TPR | FPR |
| 0 | 12 | 0 | 8 | 0 | 1.000 | 1.000 | ||
| 1 | No | 0.165 | 11 | 1 | 8 | 0 | 0.917 | 1.000 |
| 2 | Yes | 0.165 | 11 | 1 | 7 | 1 | 0.917 | 0.875 |
| 3 | Yes | 0.165 | 11 | 1 | 6 | 2 | 0.917 | 0.750 |
| 4 | Yes | 0.165 | 11 | 1 | 5 | 3 | 0.917 | 0.625 |
| 5 | Yes | 0.165 | 11 | 1 | 4 | 4 | 0.917 | 0.500 |
| 6 | No | 0.409 | 10 | 2 | 4 | 4 | 0.833 | 0.500 |
| 7 | Yes | 0.409 | 10 | 2 | 3 | 5 | 0.833 | 0.375 |
| 8 | No | 0.409 | 9 | 3 | 3 | 5 | 0.750 | 0.375 |
| 9 | No | 0.409 | 8 | 4 | 3 | 5 | 0.667 | 0.375 |
| 10 | Yes | 0.509 | 8 | 4 | 2 | 6 | 0.667 | 0.250 |
| 11 | No | 0.542 | 7 | 5 | 2 | 6 | 0.583 | 0.250 |
| 12 | No | 0.806 | 6 | 6 | 2 | 6 | 0.500 | 0.250 |
| 13 | Yes | 0.806 | 6 | 6 | 1 | 7 | 0.500 | 0.125 |
| 14 | No | 0.862 | 5 | 7 | 1 | 7 | 0.417 | 0.125 |
| 15 | No | 0.862 | 4 | 8 | 1 | 7 | 0.333 | 0.125 |
| 16 | Yes | 0.862 | 4 | 8 | 0 | 8 | 0.333 | 0.000 |
| 17 | No | 0.862 | 3 | 9 | 0 | 8 | 0.250 | 0.000 |
| 18 | No | 1.000 | 2 | 10 | 0 | 8 | 0.167 | 0.000 |
| 19 | No | 1.000 | 1 | 11 | 0 | 8 | 0.083 | 0.000 |
| 20 | No | 1.000 | 0 | 12 | 0 | 3 | 0.000 | 0.000 |
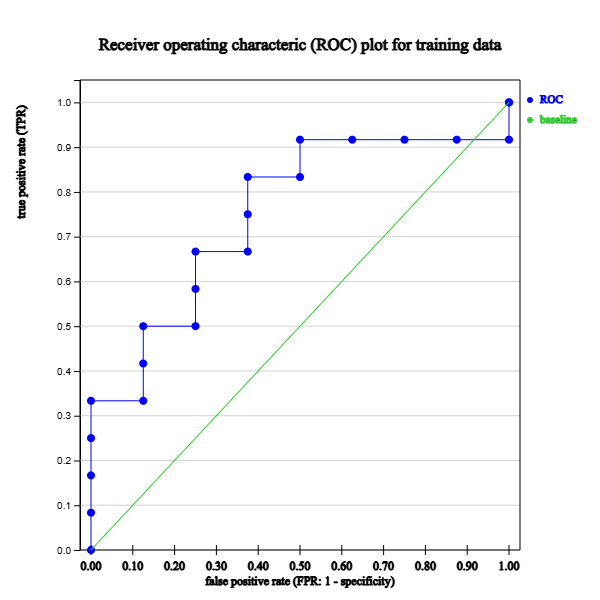
6.4.2 Comparison of classification models
In addition to accuracy, the comparison of two classification models should also consider the speed of processing the algorithm on a computer, robustness for evaluating the impact of noisy data or missing values, scalability for efficiently building the model even when a large amount of data is given, and interpretability of the model results.
Confidence interval for accuracy
Answer
When the confidence level is 95%, \(\alpha\) = 0.05, so Z_{\frac{0.05}{2}} = 1.96. The accuracy of the experiment \(\hat p\) = 0.8, and the number of data \(n\) = 100, so by substituting the confidence interval formula, we get the following. $$ \frac { ( 2 \times 100 \times 0.8 + {1.96}^2 ) \; ± \; 1.96 \sqrt{ {1.96}^2 + 4 \times 100 \times 0.8 - 4 \times 100 \times {0.8}^2 } }{2 \times 100 + 2 \times {1.96}^2} $$ That is, the 95% confidence interval of the actual accuracy is (71.1%, 86.7%).
Comparison of accuracy of two models
Answer
The number of data applied to model \(\small M_{1}\) is \(\small n_{1}\) = 50 and the accuracy is \(\small \hat p_{1}\) = 0.85, the number of data applied to model \(\small M_{2}\) is \(\small n_{2}\) = 500 and the accuracy is \(\small \hat p_{2}\) = 0.75, Therefore, the 95% confidence interval is as follows.
\( \qquad (0.85 - 0.75) \; ± \; 1.96 \sqrt{ \frac{ 0.85 (1-0.85)}{50} + \frac{ 0.75 (1-0.75)}{500}} \)
\( \qquad 0.10 ± 1.96×0.0541 \)
Therefore, the 95% confidence interval is (-0.2060, 0.0060). This confidence interval includes 0, so the difference in observed accuracy is not statistically significant. In other words, the true accuracies of model \(\small M_{1}\) and model \(\small M_{2}\) are not statistically significant, so we cannot say which classification model is better.
Generalized error considering model overfitting
6.5 Exercise
6.1 Ten data of two groups (+ group or - group) for two binary variables (A and B) are as follows.
| A | B | Group |
|---|---|---|
| T | F | + |
| T | T | + |
| T | T | + |
| T | F | - |
| T | T | + |
| F | F | - |
| F | F | + |
| F | F | - |
| T | T | + |
| T | F | - |
6.2 When we surveyed 20 people who visited a particular department store, 10 people made purchases, and 10 people did not make purchases. The survey results of these 20 people's gender (M: male, F: female, car ownership (S: small, M: medium, L: large), house ownership (Y: yes, N: no), and purchases (Y: yes, N: no) were as follows.
| Gender | Car | House | Purchase |
|---|---|---|---|
| M | M | N | Y |
| F | M | Y | N |
| F | L | Y | Y |
| F | L | Y | N |
| F | M | N | N |
| F | M | N | N |
| F | L | Y | Y |
| M | M | Y | Y |
| F | L | Y | N |
| M | L | N | Y |
| F | M | Y | Y |
| F | M | Y | N |
| M | M | N | N |
| F | M | N | Y |
| F | S | Y | N |
| F | S | N | N |
| M | S | N | Y |
| M | M | N | N |
| M | M | N | Y |
| M | S | N | N |
| F | L | Y | Y |