Chapter 7. Supervised machine learning for continuous data
[presentation] [book]
- 7.1 Bayes classification model - Continous data
- 7.1.1 R and Python practice - Bayes classification
- 7.2 Logistic regression model
- 7.2.1 R and Python practice - Logistic regression
- 7.3 Nearest neighbor classification model
- 7.3.1 R and Python practice - Nearest neighbor classification
- 7.4 Neural network model
- 7.4.1 Single-layer neural network
- 7.4.2 Multilayer neural network
- 7.4.3 Artificial intelligence
- 7.4.5 R and Python practice - Neural network
- 7.5 Support vector machine model
- 7.5.1 Linear support vector machine
- 7.5.2 Nonlinear support vector machine
- 7.5.3 R and Python practice - Support vector machine
- 7.6 Ensemble model
- 7.6.1 Bagging
- 7.6.2 R and Python practice - Bagging
- 7.6.3 Boosting
- 7.6.4 R and Python practice - Boosting
- 7.6.5 Random Forest
- 7.6.6 R and Python practice - Random forest
- 7.7 Classification of multiple groups
- 7.8 Exercise
CHAPTER OBJECTIVES
7.1 Bayes Classification Model - Continuous data
Suppose that prior probabilities of \(k\) number of groups, \(\small G_{1}, G_{2}, ... , G_{k}\), are \(\small P(G_{1}), P(G_{2}), ... , P(G_{k})\), and likelihood probability distribution functions for each group are \(\small P(X | G_{1}), P(X | G_{2}), ... , P(X | G_{k})\). Given the observation data \(\small \boldsymbol x\) for classification, let the posterior probabilities that \(\small \boldsymbol x\) comes from each group be \(\small P(G_{1} | \boldsymbol x), P(G_{2} | \boldsymbol x), ... , P(G_{k} | \boldsymbol x)\). The Bayes classification rule is as follows.
\(\qquad\) 'Classify \(\boldsymbol x\) into a group with the highest posterior probability'
If we denote the likelihood probability functions as \(\small f_{1}(\boldsymbol x), f_{2}(\boldsymbol x), ... , f_{k}(\boldsymbol x)\), since the denominators in the calculation of posterior probabilities are the same, the Bayes classification rule can be written as follows.
\(\qquad\) 'If \(\small P(G_{k}) f_{k}(\boldsymbol x) ≥ P(G_{i}) f_{i}(\boldsymbol x) \) for all \(k\) ≠ \(i\), classify \(\boldsymbol x\) into group \(\small G_{k}\)'
If there are only two groups \(\small G_{1}\)and \(\small G_{2}\), the Bayesian classification rule is expressed as follows.
\(\qquad\) 'if \( \frac{f_{1}(\boldsymbol x)}{f_{2}(\boldsymbol x)} ≥ \frac{P(G_{2})}{P(G_{1})} \), classify \(\boldsymbol x\) into group \(\small G_{1}\), else into group \(\small G_{2}\)'
A survey of customers at a computer store showed the prior probabilities of the purchasing group (\(\small G_{1}\)) and the non-purchasing group (\(\small G_{2}\)) are \(\small P(G_{1})\) = 0.4 and \(\small P(G_{2})\) = 0.6, respectively. Suppose that the likelihood distribution of the age in the purchasing group is a normal distribution with a mean of 35 and a standard deviation of 2, \(\small N(35, 2^{2})\), and the non-purchasing group is a normal distribution with a mean of 25 and a standard deviation of 2, \(\small N(25, 2^{2})\).
If a customer who visited this store on a certain day is 30 years old, classify the customer using the Bayes classification model whether he will purchase the product or not.
Answer
The functional form of the likelihood probability distribution of the purchasing group \(\small G_{1}\) and the non-purchasing group \(\small G_{2}\) are as follows. $$ \small \begin{align} P(x | G_{1}) = f_1 (x) &= \frac{1}{\sqrt{2 \pi} \; 2} \; exp \{ - \; \frac{(x - 35)^2}{2 \times 2^2} \} \\ P(x | G_{2}) = f_2 (x) &= \frac{1}{\sqrt{2 \pi} \; 2} \; exp \{ - \; \frac{(x - 25)^2}{2 \times 2^2} \} \end{align} $$ Therefore, the Bayes classification rule is as follows. $$ \small \text{If} \;\; \frac{f_1 (x)}{f_2 (x)} \;=\; exp \{ - \; \frac{(x - 35)^2}{2 \times 2^2} - \; \frac{(x - 25)^2}{2 \times 2^2} \} \; \ge \; \frac{P(G_2)}{P(G_1)} \;=\; \frac{0.6}{0.4}, \; \text{classify} \; x \; \text{into} \; G_{1}, \; \text{else} \; G_{2}. $$ If we organize the above equation by taking the log, the classification rule is as follows. $$ \small \text{If} \;\; x \ge \; 30.16, \; \text{classify} \; x \; \text{into} \; G_{1}, \; \text{else} \; G_{2}. $$ Therefore, the customer whose age is 30 is classified as a non-purchasing group (\(G_{2}\)).
| Table 7.1.1 Survey of customers on age, income, and purchasing status | |||
|---|---|---|---|
| Number | Age | Income (unit 10,000 won) |
Purchase |
| 1 | 25 | 150 | Yes |
| 2 | 34 | 220 | No |
| 3 | 27 | 210 | No |
| 4 | 28 | 250 | Yes |
| 5 | 21 | 100 | No |
| 6 | 31 | 220 | No |
| 7 | 36 | 300 | Yes |
| 8 | 20 | 100 | No |
| 9 | 29 | 220 | No |
| 10 | 32 | 250 | Yes |
| 11 | 37 | 400 | Yes |
| 12 | 24 | 120 | No |
| 13 | 33 | 350 | No |
| 14 | 30 | 180 | Yes |
| 15 | 38 | 350 | Yes |
| 16 | 32 | 250 | No |
| 17 | 28 | 240 | No |
| 18 | 22 | 220 | No |
| 19 | 39 | 450 | Yes |
| 20 | 26 | 150 | No |
Answer
The sample means of age and income of each group, \( \overline {\boldsymbol x}_1\) and \( \overline {\boldsymbol x}_2\), and sample covariance matrix \(\small \boldsymbol S\) are calculated as follows. $$ \small \qquad \overline {\boldsymbol x}_1 \; = \; \left[ \matrix{27.250 \cr 200.000} \right], \qquad \overline x_2 \; = \; \left[ \matrix{33.125 \cr 291.250} \right], \qquad \boldsymbol S \; = \; \left[ \matrix{31.621 & 470.105 \cr 470.105 & 9129.211} \right] $$ \(\small \overline {\boldsymbol x}_1 - \overline {\boldsymbol x}_2\), \(\small \boldsymbol S^{-1}\) and \(\small ( \overline {\boldsymbol x}_1 - \overline {\boldsymbol x}_2 )' \boldsymbol S^{-1}\) is as follows. $$ \small \qquad \overline {\boldsymbol x}_1 - \overline {\boldsymbol x}_2 \; = \; \left[ \matrix{-5.875 \cr -91.25} \right], \qquad \boldsymbol S^{-1} = \left[ \matrix{0.134895 & -0.006946 \cr -0.006946 & 0.000467} \right], \qquad ( \overline {\boldsymbol x}_1 - \overline {\boldsymbol x}_2 )' \boldsymbol S^{-1} = \left [ \matrix{ -0.15865 \cr -0.00182} \right ] $$ Assume that the prior probability of non-purchasing group is \(\small P(G_{1})\) = 0.6, and the prior probability of purchasing group \(\small P(G_{2})\) = 0.4, the sample linear classification function is as follows. $$ \small \text{If}\;\; (-0.15865) \times x_{1} + (-0.00182) \times x_{2} + 5.64297 \; \ge \; 0, \; \text{classify} \; \boldsymbol x = (x_{1}, x_{2}) \; \text{into} \; G_{1}, \; \text{or} \; G_{2}. $$ If the visiting customer's age is 33 and income is 200, the classification function becomes as follows. $$ \small (-0.15865)*(33) + (0.00182) * (200) + (5.64297) = 0.04251 $$ Therefore, the customer is classified into the non-purchasing group \(\small G_{1}\).
[]
Variable selection
Characteristics of Bayes classification
7.1.1 R and Python practice - Bayes classification
R practice
[Colab]
| Fit a linear discriminant analysis model. |
|
|---|---|
|
lda(x, ...) ## S3 method for class 'formula' lda(formula, data, ..., subset, na.action) ## Default S3 method: lda(x, grouping, prior = proportions, tol = 1.0e-4,method, CV = FALSE, nu, ...) ## S3 method for class 'data.frame' lda(x, ...) ## S3 method for class 'matrix' lda(x, grouping, ..., subset, na.action) |
|
| formula | A formula of the form groups ~ x1 + x2 + ... That is, the response is the grouping factor and the right hand side specifies the (non-factor) discriminators. |
| data | Data frame from which variables specified in formula are preferentially to be taken. |
| x | (required if no formula is given as the principal argument.) a matrix or data frame or Matrix containing the explanatory variables. |
| grouping | (required if no formula principal argument is given.) a factor specifying the class for each observation. |
| prior | the prior probabilities of class membership. If unspecified, the class proportions for the training set are used. If present, the probabilities should be specified in the order of the factor levels. |
| tol | A tolerance to decide if a matrix is singular; it will reject variables and linear combinations of unit-variance variables whose variance is less than tol^2. |
| subset | An index vector specifying the cases to be used in the training sample. (NOTE: If given, this argument must be named.) |
| na.action | A function to specify the action to be taken if NAs are found. The default action is for the procedure to fail. An alternative is na.omit, which leads to rejection of cases with missing values on any required variable. |
| method | "moment" for standard estimators of the mean and variance, "mle" for MLEs, "mve" to use cov.mve, or "t" for robust estimates based on a t distribution. |
An example of R commands for a Bayes classification with purchase as the dependent variable of card data and other variables as independent variables is as follows.
| install.packages('MASS') |
| library(MASS) |
| customer <- read.csv('http://estat.me/estat/Example/DataScience/PurchaseByCredit20_Continuous.csv', header=T, as.is=FALSE) |
| attach(customer) |
Purchase[1] Yes No No Yes No No Yes No No Yes Yes No No Yes Yes No No No Yes [20] No Levels: No Yes |
| ldamodel <- lda(Purchase ~ ., customer) |
ldamodel
Call: lda(Purchase ~ ., data = customer)
Prior probabilities of groups:
No Yes
0.6 0.4
Group means:
Age Income
No 27.250 200.00
Yes 33.125 291.25
Coefficients of linear discriminants:
LD1
Age 0.173328870
Income 0.001994526
|
| pred <- predict(ldamodel, customer)" |
pred$class
$class [1] No Yes No No No No Yes No No No Yes No Yes No Yes No No No Yes [20] No Levels: No Yes |
classtable <- table(Purchase,pred$class)
Purchase No Yes
No 10 2
Yes 4 4
|
sum(diag(classtable)) / sum(classtable)
[1] 0.7 |
Python practice
[Colab]
|
# Import required libraries import pandas as pd customer = pd.read_csv('https://raw.githubusercontent.com/ogut77/DataScience/refs/heads/main/PurchaseByCredit20_Continuous.csv')
Age Income Purchase
0 25 150 Yes
1 34 220 No
2 27 210 No
3 28 250 Yes
4 21 100 No
5 31 220 No
6 36 300 Yes
7 20 100 No
8 29 220 No
9 32 250 Yes
10 37 400 Yes
11 24 120 No
12 33 350 No
13 30 180 Yes
14 38 350 Yes
15 32 250 No
16 28 240 No
17 22 220 No
18 39 450 Yes
19 26 150 No
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis # Separate features (X) and target variable (y) X = customer.drop('Purchase', axis=1) y = customer['Purchase'] # Initialize and train the Linear Discriminant Analysis model lda = LinearDiscriminantAnalysis() lda.fit(X, y) # Make predictions on the test set y_pred = lda.predict(X) # Evaluate the model (example: accuracy) # You would typically use more comprehensive evaluation metrics # depending on your specific needs. from sklearn.metrics import accuracy_score from sklearn.metrics import confusion_matrix accuracy = accuracy_score(y, y_pred) cm=confusion_matrix(y, y_pred) print(f"Accuracy: {accuracy}") print(f"Confusion Matrix: \n{cm}") Accuracy: 0.7 Confusion Matrix: [[10 2] [ 4 4]] |
7.2 Logistic regression model
When the target variable has the values 1 and 0, the logistic regression model is a linear regression of the log value of the odds ratio, which is the ratio of the probability \(\small P(Y = 1 \;| x) \) and the probability \(\small P(Y = 0 \;| x) \) given that \(\small X = x \), as shown below. $$ \small ln \; \frac{P(Y = 1 \;| x)}{P(Y = 0 \;| x)} = \alpha + \beta x $$ Here, \(ln\) is the natural logarithm and \(\small P(Y = 0 \;| x) = 1 - P(Y = 1 \;| x) \). If we rearrange the above equation using \(\small P(Y = 1 \;| x) \), it can be written as follows. $$ \small P(Y = 1 \;| x) = \frac {exp(\alpha + \beta x)}{1 + exp(\alpha + \beta x)} $$ It means that, if the coefficients \(\small \alpha\) and \(\small \beta\) of this regression model can be estimated using the least squares method, \(\small P(Y = 1 \;| x) \) can also be estimated. The estimated probability \(\small P(Y = 1 \;| x) \) is called the posterior probability of the group 1, and \(\small P(Y = 0 \;| x) \) is called the posterior probability of the group 0. Data is classified into the group 1 if this posterior probability value is greater than a critical value selected by the analyst, such as 0.5, otherwise it is classified as group 0. The maximum likelihood estimation method is frequently used to estimate the coefficient of the logistic regression model.
The above simple logistic regression model with one variable can be extended to have \(m\) variables as follow. $$ \small ln \; \frac{P(Y = 1 \;|\; \boldsymbol x = (x_{1},x_{2}, ... , x_{m}) )}{1 - P(Y = 1 \;|\; \boldsymbol x = (x_{1},x_{2}, ... , x_{m}))} = \beta_{0} + \beta_{1} X_{1} + \beta_{2} X_{2} + \cdots \beta_{m} X_{m} $$ If we rearrange the above equation using \(\small P(Y = 1 \;|\; \boldsymbol x = (x_{1},x_{2}, ... , x_{m}) ) \), it can be written as follow. $$ \small P(Y = 1 \;|\; \boldsymbol x = (x_{1}, x_{2}, ... ,x_{m}) ) = \frac {exp(\beta_{0} + \beta_{1} X_{1} + \beta_{2} X_{2} + \cdots + \beta_{m} X_{m})}{1 + exp(\beta_{0} + \beta_{1} X_{1} + \beta_{2} X_{2} + \cdots + \beta_{m} X_{m})} $$ Given the data \(\small \boldsymbol x = (x_{1}, x_{2}, ... ,x_{m})\) to be classified, the posterior probability \(\small P(Y = 1 \;|\; \boldsymbol x = (x_{1},x_{2}, ... , x_{m}) ) \) is estimated using the estimated regression coefficients of \(\small \beta_{0}, \beta_{1}, ... ,\beta_{m}\). If the estimated posterior probability is greater than the critical value selected by the analyst, it is classified as group 1, otherwise it is classified as group 0.
Let us examine the effect of independent variable \(\small X_{i}\) on the classification of groups in the logistic regression model. If all other variables are constant and only the variable value \(\small x_{i}\) is increased by 1 unit (\(\small x_{i} + 1\)), the incremental odds ratio is as follows. $$ \small \begin{align} \text{Incremental odds ratio} &= \frac{exp(\beta_{0} + \beta_{1} x_{1} + \cdots + \beta_{i} (x_{i}+1) + \cdots + \beta_{m} x_{m})}{exp(\beta_{0} + \beta_{1} x_{1} + \cdots + \beta_{i} x_{i} + \cdots + \beta_{m} x_{m})} \\ &= exp(\beta_{i}) \end{align} $$ Therefore, when the variable \(\small X_{i}\) increases by 1 unit, if \(\small \beta_{i}\) is positive, the odds ratio increase rate is greater than 1, so \(\small P(Y = 1 \;|\; \boldsymbol x = (x_{1},x_{2}, ... , x_{m}) ) \) also increases. On the other hand, if \(\small \beta_{i}\) is negative, the odds ratio increase rate is less than 1, so \(\small P(Y = 1 \;|\; \boldsymbol x = (x_{1},x_{2}, ... , x_{m}) ) \) decreases. For example, monthly income \(\small X\) is an independent variable and customer purchasing status \(\small Y\) is the target variable, such as purchasing a product (\(\small Y = 1\)) or not (\(\small Y = 0\)). The estimated logistic regression model is as follow. $$ \small ln \; \frac{P(Y = 1 \;| x)}{1 - P(Y = 1 \;| x)} = 0.21 + 1.34 x $$ In this case, if the monthly income \(\small X\) increases by 1 unit, the odds ratio increase rate becomes \(exp(1.34)\) = 3.82. That is, if monthly income increases by 1 unit, the odd ratio of the probability of purchasing a product to the probability of not purchasing it increases by 3.82 times.
In the case of a logistic regression model with many independent variables, the variable that best explains the target variable must be selected. In order to select variables, a model selection criterion that can compare several models is needed, and the Akaike Information Criteria (AIC) is commonly used. Specific selection methods include forward selection, backward elimination, and stepwise methods, as in the Bayes classification variable selection method. For more information, please refer to a related statistics book.
Answer
If we perform a logistic regression analysis using R with age (\(\small X_{1}\)) and monthly income (\(\small X_{2}\)) as independent variables and purchasing status as a target variable (\(\small Y\)), we will get the results in the following table.
| Coefficients: | ||
| (Intercept) | Age | Income |
| -7.629959 | 0.223517 | 0.001918 |
This means that the logistic regression model is as follows. $$ \small ln \; \frac{P(Y = 1 \;|\; \boldsymbol X = (X_{1}, X_{2}) )}{1 - P(Y = 1 \;|\; \boldsymbol X = (X_{1}, X_{2}))} = -7.629959 + 0.223517 X_{1} + 0.001918 X_{2} $$ If we rearrange the above equation using \(\small P(Y = 1 \;|\; \boldsymbol X = (X_{1}, X_{2}) ) \), it can be written as follows. $$ \small P(Y = 1 \;|\; \boldsymbol X = (X_{1}, X_{2}) ) = \frac {exp(-7.629959 + 0.223517 X_{1} + 0.001918 X_{2} )}{1 + exp(-7.629959 + 0.223517 X_{1} + 0.001918 X_{2} )} $$ If a customer whose age is 20 and income is 200, \(\small \boldsymbol X = (20, 200) \), the posterior probability \(\small P(Y = 1 \;|\; \boldsymbol X ) \) is as follows. $$ \small \begin{align} P(Y = 1 \;|\; \boldsymbol X = (20, 200) ) &= \frac {exp(-7.629959 + 0.223517 \times 20 + 0.001918 \times 200 )}{1 + exp(-7.629959 + 0.223517 \times 20 + 0.001918 \times 200 )} \\ &= \frac{0.062286}{1 + 0.062286 } \\ &= 0.058634 \end{align} $$ If the critical value of the posterior probability is 0.5, then the customer is classified by group 0, which is the non-purchasing group.
7.2.1 R and Python practice - Logistic regression
R practice
[Colab]
File > Change Directory > C: > Rwork
If we read the data file in R, it looks like as follows.
| # read the data file |
| customer <- read.csv('http://estat.me/estat/Example/DataScience/PurchaseByCredit20_Continuous.csv', header=T, as.is=FALSE) |
customer
Age Income Purchase
1 25 150 Yes
2 34 220 No
3 27 210 No
4 28 250 Yes
5 21 100 No
6 31 220 No
7 36 300 Yes
8 20 100 No
9 29 220 No
10 32 250 Yes
11 37 400 Yes
12 24 120 No
13 33 350 No
14 30 180 Yes
15 38 350 Yes
16 32 250 No
17 28 240 No
18 22 220 No
19 39 450 Yes
20 26 150 No
|
| attach(customer) |
Purchase
[1] Yes No No Yes No No Yes No No Yes Yes No No Yes Yes No No No Yes [20] No Levels: No Yes |
| logitmodel <- glm(Purchase ~.,family=binomial(link='logit'),data=card) |
logitmodel
Call: glm(formula = Purchase ~ ., family = binomial(link = "logit"), data = card) Coefficients: (Intercept) Age Income -7.629959 0.223517 0.001918 Degrees of Freedom: 19 Total (i.e. Null); 17 Residual Null Deviance: 26.92 Residual Deviance: 20.68 AIC: 26.68 |
Python practice
[Colab]
|
# Import required libraries import pandas as pd from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score, confusion_matrix # Load the dataset (assuming it's already loaded as 'customer') # If not, uncomment the line below customer = pd.read_csv('https://raw.githubusercontent.com/ogut77/DataScience/refs/heads/main/PurchaseByCredit20_Continuous.csv') # Separate features (X) and target variable (y) X = customer.drop('Purchase', axis=1) y = customer['Purchase'] # Initialize and train the Logistic Regression model logreg = LogisticRegression() # Specify a solver logreg.fit(X, y) print(logreg) # Make predictions on the test set y_pred = logreg.predict(X) # Evaluate the model accuracy = accuracy_score(y, y_pred) cm = confusion_matrix(y, y_pred) print(f"Accuracy: {accuracy}") print(f"Confusion Matrix:\n{cm}") |
7.3 Nearest neighbor classification model
<Figure 7.3.1> shows two-dimensional continuous data divided into + and - groups. When the data marked with \(\small X\) in the Figure is to be classified, it shows the 1-nearest neighbor (innermost circle), 2-nearest neighbor (middle circle), and 7-nearest neighbor (outer circle) data points using the two-dimensional Euclidean distance.
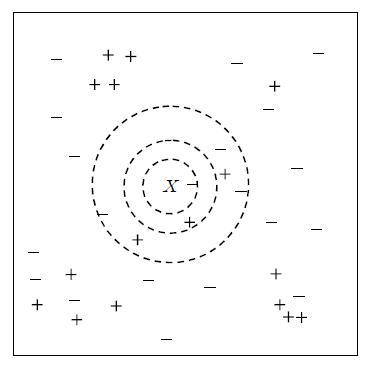
If only 1-nearest neighbor is used for classification, there is one - group, and the data \(\small X\) is classified as the - group. If 2-nearest neighbors are used, there are one + group and one - group data, so it is difficult to classify the data \(\small X\) and it can be classified into either group. If 7-nearest neighbors are used, since there are three + groups and four - groups, the majority rule is used to classify \(\small X\) into the - group. As seen in these cases, the appropriate selection of \(k\) has a great influence on the classification result. If \(k\) is too small, the data may be incorrectly classified due to the noise of the data. If \(k\) is too large, the data may not be classified into a group close to the data.
An algorithm for the nearest neighbor classification model can be summarized as follows.
Suppose there are \(n\) number of training data with \(m\) variables \(\boldsymbol x_{i}\) and group variable \(y_i\) as \(\small D = \{(\boldsymbol x_{1}, y_{1}),(\boldsymbol x_{2}, y_{2}), ... , (\boldsymbol x_{n}, y_{n}) \}\). The algorithm first calculates the similarity distance between the test data \(\boldsymbol x\) to be classified and all training data. If there is a lot of training data, the calculation of the similarity distance may take a lot of time. After finding the \(k\) adjacent neighbors \(\small D_{\boldsymbol x}\) using the calculated distance, the test data \(\boldsymbol x\) is classified into a majority group of these adjacent neighbors, which can be expressed in the following formula. $$ \small y = {argmax}_{v} \; \sum_{(\boldsymbol x_{i}, y_{i}) \in D_{\boldsymbol x}} \; I (v=y_{i}) $$
| Step 1 | Let \(\boldsymbol x\) be the test data, and \(D = \{(\boldsymbol x_{1}, y_{1}),(\boldsymbol x_{2}, y_{2}), ... , (\boldsymbol x_{n}, y_{n}) \}\) be the training data. |
| Step 2 | for test data \(\boldsymbol x\) do |
| Step 3 | \(\qquad\)for i = 1 to n do |
| Step 4 | \(\qquad \qquad\)Calculate the distance \(d(\boldsymbol x, \boldsymbol x_{i})\) between \(\boldsymbol x\) and \(\boldsymbol x_{i}\) |
| Step 5 | \(\qquad\)end for |
| Step 6 | \(\qquad\)Find the training data set \(D_{\boldsymbol x}\) that is the \(k\) nearest neighbor of \(\boldsymbol x\) |
| Step 7 | \(\qquad\)Classify \(\boldsymbol x\) into the majority group of \(D_{\boldsymbol x}\), that is \(\qquad\qquad y = {argmax}_{v} \; \sum_{(\boldsymbol x_{i}, y_{i}) \in D_{\boldsymbol x}} \; I (v=y_{i})\) |
| Step 8 | end for |
Answer
Age and monthly income have different measurement units, so they must be converted to the same unit. Here, the standardization transformation was used using the sample average of age 29.6 and its sample standard deviation of 5.623, and the sample average of monthly income 236.5, and sample standard deviation 95.547 as Table 7.3.1. The standardized value of the customer's data (33, 190) becomes (0.605, -0.487), and Table 7.3.1 shows the squared Euclidean distance between the customer data and all data. 5-nearest neighbors were colored as yellow background which included 3 of 'No's and 2 of 'Yes's. Therefore, the customer is classified into 'No" which means he will not purchase a product.
| Table 7.3.1 Standardized data of age and income, and squared Euclid distance of the customer | ||||||
|---|---|---|---|---|---|---|
| Number | Age | Income (unit 10,000 won) |
Purchase | Standardized Age |
Standardized Income |
Squared Euclid Distance of customer |
| 1 | 25 | 150 | Yes | -0.818 | -0.905 | 2.199 |
| 2 | 34 | 220 | No | 0.782 | -0.173 | 0.130 |
| 3 | 27 | 210 | No | -0.462 | -0.277 | 1.182 |
| 4 | 28 | 250 | Yes | -0.285 | 0.141 | 1.185 |
| 5 | 21 | 100 | No | -1.529 | -1.429 | 5.441 |
| 6 | 31 | 220 | No | 0.249 | -0.173 | 0.225 |
| 7 | 36 | 300 | Yes | 1.138 | 0.665 | 1.610 |
| 8 | 20 | 100 | No | -1.707 | -1.429 | 6.232 |
| 9 | 29 | 220 | No | -0.107 | -0.173 | 0.605 |
| 10 | 32 | 250 | Yes | 0.427 | 0.141 | 0.426 |
| 11 | 37 | 400 | Yes | 1.316 | 1.711 | 5.337 |
| 12 | 24 | 120 | No | -0.996 | -1.219 | 3.098 |
| 13 | 33 | 350 | No | 0.605 | 1.188 | 2.804 |
| 14 | 30 | 180 | Yes | 0.071 | -0.591 | 0.296 |
| 15 | 38 | 350 | Yes | 1.494 | 1.188 | 3.595 |
| 16 | 32 | 250 | No | 0.427 | 0.141 | 0.426 |
| 17 | 28 | 240 | No | -0.285 | 0.037 | 1.064 |
| 18 | 22 | 220 | No | -1.352 | -0.173 | 3.925 |
| 19 | 39 | 450 | Yes | 1.672 | 2.235 | 8.543 |
| 20 | 26 | 150 | No | -0.640 | -0.905 | 1.725 |
Selection of \(k\) on the neighbor classification
[Nearest neighbor classification]
Characteristics of the neighbor classification model
7.3.1 R and Python practice - Nearest neighbor classification
R practice
[Colab]
| k-nearest neighbor classification model. This function provides a formula interface to the existing knn() function of package class. On top of this type of convinient interface, the function also allows standardization of the given data. |
|
|---|---|
| kNN(form, train, test, stand = TRUE, stand.stats = NULL, ...) | |
| form | An object of the class formula describing the functional form of the classification model. |
| train | The data to be used as training set. |
| test | The data set for which we want to obtain the k-NN classification, i.e. the test set. |
| stand | A boolean indicating whether the training data should be previously normalized before obtaining the k-NN predictions (defaults to TRUE). |
| stand.stats | This argument allows the user to supply the centrality and spread statistics that will drive the standardization. If not supplied they will default to the statistics used in the function scale(). If supplied they should be a list with two components, each beig a vector with as many positions as there are columns in the data set. The first vector should contain the centrality statistics for each column, while the second vector should contain the spread statistc values. |
An example of R commands for a k-neares neighbor classification with customer data as both training and testing when k= 5 is as follows.
| install.packages('DMwR2') |
| library(DMwR2) |
| customer <- read.csv('http://estat.me/estat/Example/DataScience/PurchaseAgeIncome_Continuous.csv', header=T, as.is=FALSE) |
| attach(customer) |
Purchase
[1] Yes No No Yes No No Yes No No Yes Yes No No Yes Yes No No No Yes [20] No Levels: No Yes |
| nn <- kNN(Purchase ~ ., customer, customer, k=5) |
nn
[1] No No No No No No Yes No No No Yes No Yes No Yes No No No Yes No Levels: No Yes |
To make a classification cross table, we can use a vector of Purchase and nn which is the predicted class with table command as below. Using this classification table, accuracy of the model is calculated as 0.75 which is (11+4) / (11+1+4+4).
classtable <- table(Purchase, nn)
Purchase No Yes
No 11 1
Yes 4 4
|
sum(diag(classtable)) / sum(classtable)
[1] 0.75 |
Python practice
[Colab]
|
# Import required libraries import pandas as pd from sklearn.metrics import accuracy_score, confusion_matrix from sklearn.neighbors import KNeighborsClassifier customer = pd.read_csv('https://raw.githubusercontent.com/ogut77/DataScience/refs/heads/main/PurchaseByCredit20_Continuous.csv') # Separate features (X) and target variable (y) X = customer.drop('Purchase', axis=1) y = customer['Purchase'] # Initialize and train the KNN model knn = KNeighborsClassifier(n_neighbors=5) # You can adjust the number of neighbors knn.fit(X, y) # Make predictions on the test set y_pred = knn.predict(X) # Evaluate the model accuracy = accuracy_score(y, y_pred) cm = confusion_matrix(y, y_pred) print(f"KNN Accuracy: {accuracy}") print(f"KNN Confusion Matrix:\n{cm}") |
7.4 Artificial neural network model
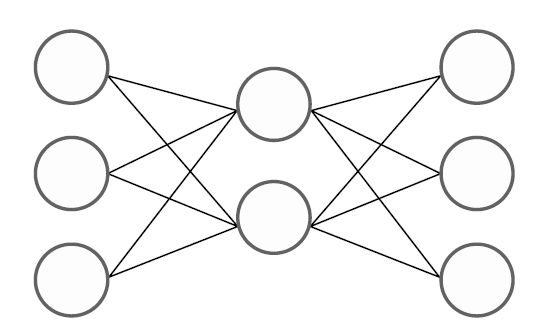
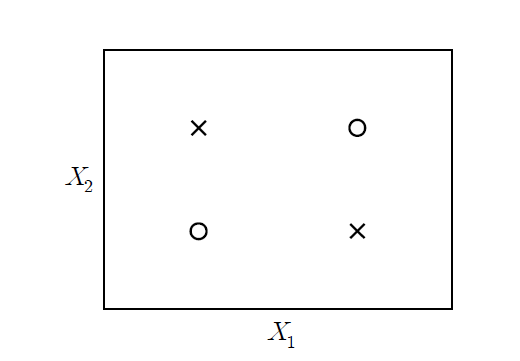
The artificial neural network model is a model that uses a generalized nonlinear function as a classification function. The motivation for studying this model is the simple two-group (denoted as o and x) two-dimensional data as in <Figure 7.4.2>. This data cannot be separated into two groups o and x by a single straight line (not linearly separable), and can only be separated by two straight lines or nonlinear functions.
7.4.1 Single-layer neural network
Suppose \(y\) is a group variable where there are two groups, denoted '+1' and '-1', and there are three binary variables \(x_{1}, x_{2}, x_{3}\) which have values either 0 or 1. If two or more of the three binary variables have the value 1, classify them as the group ‘+1’, and if they have one or fewer 1 value, classify them as the group ‘-1’ as in Table 7.4.1. Create a single-layer neural network model that can perform such classification and classify this data.
| Table 7.4.1 Possible values of three binary variables \(x_{1}, x_{2}, x_{3}\) and their group \(y\) | ||||
|---|---|---|---|---|
| Number | \(x_{1}\) | \(x_{2}\) | \(x_{3}\) | \(y\) |
| 1 | 0 | 0 | 0 | -1 |
| 2 | 0 | 0 | 1 | -1 |
| 3 | 0 | 1 | 0 | -1 |
| 4 | 0 | 1 | 1 | +1 |
| 5 | 1 | 0 | 0 | -1 |
| 6 | 1 | 0 | 1 | +1 |
| 7 | 1 | 1 | 0 | +1 |
| 8 | 1 | 1 | 1 | +1 |
Answer
If the predicted value of the group is \(\hat y\), the above data can be classified using the following linear function model. $$ \small \hat y = \{ \array {\; +1 \quad & if \;\; 0.3 x_{1} + 0.3 x_{2} + 0.3 x_{3} - 0.4 > 0 \cr \; -1 \quad & if \;\; 0.3 x_{1} + 0.3 x_{2} + 0.3 x_{3} - 0.4 < 0 } \ $$ For example, if \(\small x_{1} = 1, \; x_{2} = 1, \; x_{3} = 0 \), then \(\small 0.3 x_{1} + 0.3 x_{2} + 0.3 x_{3} - 0.4 = 0.2\), so \(\hat y\) = +1. If \(\small x_{1} = 0, \; x_{2} = 1, \; x_{3} = 0 \), then \(\small 0.3 x_{1} + 0.3 x_{2} + 0.3 x_{3} - 0.4 = -0.1 \), so \(\hat y\) = -1. Let us put aside the discussion of how to create such a linear classification model for a moment and if we represent the above model as a neural network in an easy-to-understand way, it is as in <Figure 7.4.3>. This is called a single-layer neural network or perceptron.
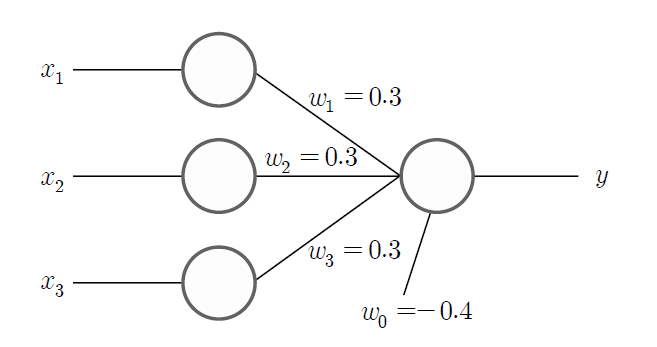
As you can see in the figure, there is an input node to display the value of three variables \(\small x_{1}, \; x_{2}, \; x_{3} \) and the output node of the model to display the value of the group variable \(\small y\). The nodes are also called neurons in neural networks as the human brain. Each input node is connected to the output node with a weight coefficient, which describes the connections between neurons in the brain. Just as neurons in the brain can learn and make decisions, neural networks use data to train the optimal weight coefficients (in the figure, \(\small w_{1} = 0.3, w_{2} = 0.3, w_{3} = 0.3 \)) that connect the relationship between input nodes and output nodes. The output node of the neural network calculates the value \(\hat y\) of the group by adding a constant \(\small w_{0} = -0.4\) to the linear combination using the weight coefficients of each input node to calculate the value \(\small w_{0} + w_{1}x_{1} + w_{2}x_{2} + w_{3}x_{3}\), which is called a linear combination function. The constant \(\small w_{0}\) is called a bias factor. The sign function \(sign(x)\) is used to investigate the sign of the calculated linear combination function value which is called an activation function.
In the example above, a weighted sum of input information was used as the combination function, but there are other combination functions such as simple sums of input information, maximum values, minimum values, or logical ANDs and ORs, but the weighted sum is the most commonly used. In addition to the sign function \(sign(x)\), examples of frequently used activation functions are as in Table 7.4.2, and <Figure 7.4.4> shows shapes of these activation functions.
| Table 7.4.2 Examples of activation functions | ||
|---|---|---|
| Name | Activation fuction | Range |
| \(sign\) function | \(y = sign(x)\) | -1, +1 |
| \(sigmoid\) fuction | \(y = \frac{1}{1+e^{-x}}\) | (0, 1) |
| \(tanh\) function | \(y = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}\) | (-1, 1) |
| \(Gauss\) function | \(y = e^{-\frac{x^2}{2}}\) | (0, 1) |
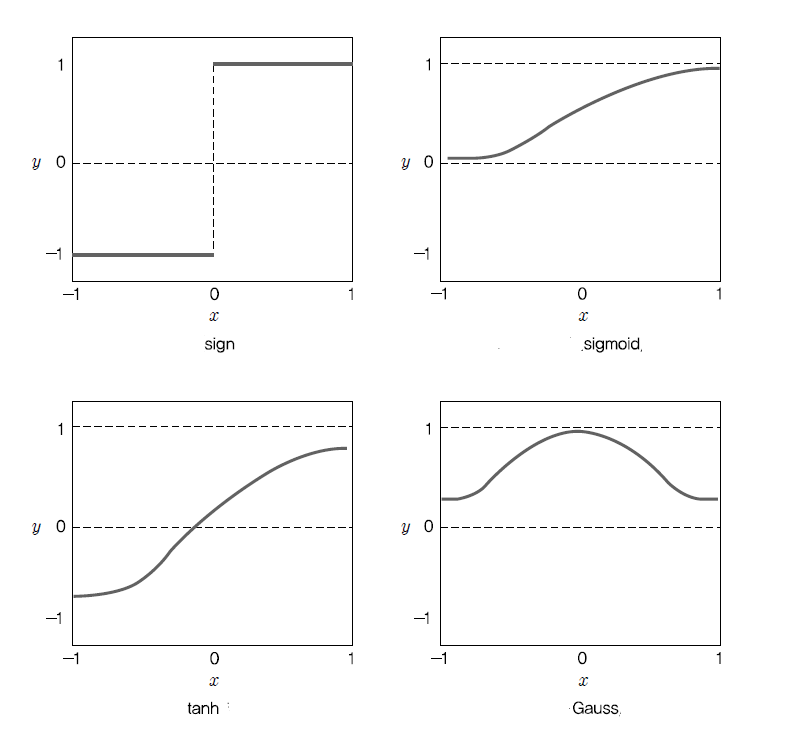
Learning algorithm for single layer neural network
| Step 1 | Let \(D = \{ (x_{i1}, x_{i2}, ... , x_{im}, y_{i}),\; i=1,2,..., n \}\) be the training data |
| Step 2 | \(w_{1}^{(0)}, w_{2}^{(0)}, ... , w_{m}^{(0)}\) be the initial estimated value of the coefficients and \(\lambda\) is the learning rate |
| Step 3 | for i = 1 to n do |
| Step 4 | \(\qquad\)for j = 1 to m do |
| Step 5 | \(\qquad \qquad\)Estimate \(y_{i}^{(i)}\) using \(w_{1}^{(i-1)}, w_{2}^{(i-1)}, ... , w_{m}^{(i-1)}\) |
| Step 6 | \(\qquad \qquad\)\(w_{j}^{(i)} = w_{j}^{(i-1)} + \lambda (y_{i} - y_{i}^{(i)}) x_{ij} \) |
| Step 7 | \(\qquad\)end for |
| Step 8 | end for |
The above search method is an algorithm that finds weighting coefficients which minimize the sum of square errors when the estimated value \(\hat y_{i}\) for each data group is found using the linear combination function \(w_{0} + w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{m}x_{m} \) and the sigmoid activation function. The sum of squared errors in a single-layer neural network with \(m+1\) weighting coefficients \(\boldsymbol w = (w_{0}, w_{1}, w_{2}, ... , w_{m})\) is as follows. $$ E(\boldsymbol w) = \sum_{i=1}^{n} \; (y_{i} - \hat y_{i})^2 $$ In order to find \(\boldsymbol w = (w_{0}, w_{1}, w_{2}, ... , w_{m})\) that minimizes the sum of squared errors, we can differentiate \(E(\boldsymbol w)\) partially with respect to each \(w_{j}\) as follows. $$ \frac{\partial E(\boldsymbol w)}{\partial w_{j}} = -2 \; \sum_{i=1}^{n} \; (y_{i} - \hat y_{i}) \frac{\partial \hat y_{i}}{\partial w_{j}} $$ Therefore, one way to search for the weight coefficient \(w_{j}\) that minimizes the sum of squared errors is to move in the direction of the partial derivatives as follows. $$ w_{j} \;←\; w_{j} \;-\; \lambda \; \frac{\partial E(\boldsymbol w)}{\partial w_{j}} $$ In the case of the linear combination function and sigmoid activation function, the algorithm for searching weight coefficients can be created as follows. $$ w_{j} \;←\; w_{j} \;-\; \lambda \; (y_{i} - \hat y_{i}) x_{ij} $$ For more information on the algorithm, please refer to the relevant literature, and let us examine the learning of a single-layer neural network using the following example.
Answer
Table 7.4.3 is the application of the learning algorithm to the single-layer neural network, which calculates the weighted linear combination \(\small \boldsymbol w^{(i)} = w_{0} + w_{1}^{(i-1)}x_{1} + w_{2}^{(i-1)}x_{2} + w_{3}^{(i-1)}x_{3}\) and the estimation of group value \(\small \hat y_{i} = sign(\boldsymbol w^{(i)})\) using the given initial values.
| Table 7.4.3 Application of learning algorithm to the sigle-layer neural network | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| iteration | data | linear combination function | activation function | modified coefficients | |||||
| i | \(x_{i1}\) | \(x_{i2}\) | \(x_{i3}\) | \(y_{i}\) | \(\small \boldsymbol w^{(i)} = w_{0} + w_{1}^{(i-1)}x_{1} + w_{2}^{(i-1)}x_{2} + w_{3}^{(i-1)}x_{3}\) | \(\small \hat y_{i} = sign(\boldsymbol w^{(i)})\) | \(w_{1}^{(i)}\) | \(w_{2}^{(i)}\) | \(w_{3}^{(i)}\) |
| 1 | 0 | 0 | 0 | -1 | -0.4 | -1 | 0.2 | 0.1 | 0.1 |
| 2 | 0 | 0 | 1 | -1 | -0.3 | -1 | 0.2 | 0.1 | 0.1 |
| 3 | 0 | 1 | 0 | -1 | -0.3 | -1 | 0.2 | 0.1 | 0.1 |
| 4 | 0 | 1 | 1 | +1 | -0.2 | -1 | 0.2 | 0.3 | 0.3 |
| 5 | 1 | 0 | 0 | -1 | -0.2 | -1 | 0.2 | 0.3 | 0.3 |
| 6 | 1 | 0 | 1 | +1 | 0.1 | +1 | 0.2 | 0.3 | 0.3 |
| 7 | 1 | 1 | 0 | +1 | 0.1 | +1 | 0.2 | 0.3 | 0.3 |
| 8 | 1 | 1 | 1 | +1 | 0.4 | +1 | 0.2 | 0.3 | 0.3 |
Looking at the table, if the actual group value \(\small y_{i}\) and the estimated value \(\small \hat y_{i}\) are the same, there is no change in the weight coefficient (iterations 1, 2, and 3). In iteration 4, since the error is (\(\small y_{4} - \hat y_{4}\)) = 2, the weight coefficient of the variable with \(\small x_{2}\) = 1 and \(\small x_{3}\) = 1 is increased by \(\small \lambda \times (y_{4} - \hat y_{4}) \times x_{4j}\) = 0.2. Since the other data have the same group value and predicted value, there is no change in the weight coefficient, so the estimated final weight coefficient is \(w_{1}\) = 0.2, \(w_{2}\) = 0.3, \(w_{3}\) = 0.3. That is, the final neural network model is \(\small \hat y = sign( -0.4 + 0.2 x_{1} + 0.3 x_{2} + 0.3 x_{3} )\). If this estimation formula is applied to all data, the groups are accurately classified.
It should be noted that the estimation algorithm for the weight coefficients of a single-layer neural network can have different solutions depending on the initial value and learning rate. For example, if the initial values are the same and the learning rate is \(\lambda\) = 0.05, the final weight coefficients are \(w_{1}\) = 0.2, \(w_{2}\) = 0.25, \(w_{3}\) = 0.25, and this solution also correctly classifies all data.
7.4.2 Multilayer neural network
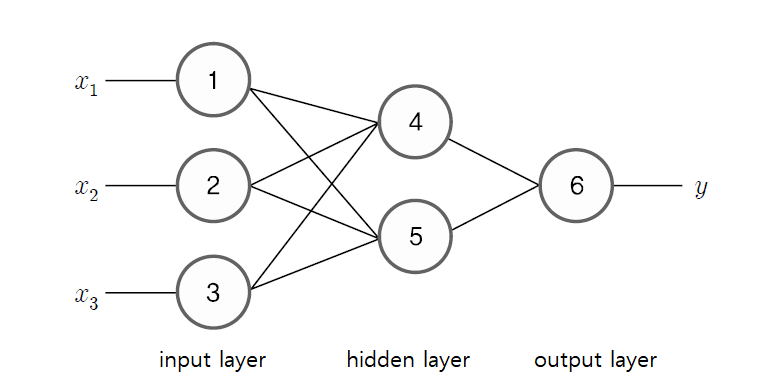
The neural network in <Figure 7.4.5> can be expressed as a formula as follows. Let the weight coefficients from the input node ① to the hidden nodes ④ and ⑤ be \(w_{14}\) and \(w_{15}\), let the weight coefficients from the input node ② to the hidden nodes ④ and ⑤ be \(w_{24}\) and \(w_{25}\), and let the weight coefficients from the input node ③ to the hidden nodes ④ and ⑤ be \(w_{34}\) and \(w_{35}\). In the same way, let the weight coefficient from the hidden node ④ to the output node ⑥ be \(w_{46}\), and let the weight coefficient from the hidden node ⑤ to the output node ⑥ be \(w_{56}\). And if the bias constants of nodes ④, ⑤, and ⑥ are \(w_{04}, w_{05}, w_{06}\) and the activation function is \(f_{4}, f_{5}, f_{6}\), then the output values \(O_{4}\) and \(O_{5}\) calculated from hidden nodes ④ and ⑤ are as follows. $$ \begin{align} O_{4} &= f_{4} ( w_{04} + w_{14} x_{1} + w_{24} x_{2} + w_{34} x_{3} ) \\ O_{5} &= f_{5} ( w_{05} + w_{15} x_{1} + w_{25} x_{2} + w_{35} x_{3} ) \end{align} $$ The value of the output node ⑥, i.e., the estimated value of \(y\), is the value of the activation function for linear combination of \(O_{4}\) and \(O_{5}\) as follows. $$ \hat y = f_{6} ( w_{06} + w_{46} O_{4} + w_{56} O_{6} ) $$ If we combine the above equations, the estimated value of \(y\) becomes the following complex nonlinear function. $$ \hat y = f_{6} ( w_{06} + w_{46} f_{4} ( w_{04} + w_{14} x_{1} + w_{24} x_{2} + w_{34} x_{3} ) + w_{56} f_{5} ( w_{05} + w_{15} x_{1} + w_{25} x_{2} + w_{35} x_{3} ) ) $$
- How many hidden layers should there be?
- How many nodes should each hidden layer have?
- Is there a nonlinear function represented by these hidden layers and hidden nodes?
When a continuous function \(f(\boldsymbol x)\) is defined on \([0,1]^{m}\), this function can be expressed as follows. $$ f(\boldsymbol x) = \sum_{k=1}^{2m+1} \; \Theta_{k} \left[ \sum_{j=1}^{m} \; \phi_{jk} (x_{j}) \right] $$ Here, \(\Theta_{k}\) and \(\phi_{jk}\) are appropriately chosen functions.
Design of multilayer neural network model
In the case of continuous variables, units of variables may be different, so the variable values are usually converted to be between 0 and 1. A simple conversion method is to subtract the minimum value from the actual data value and then divide it by the possible range of the variable (maximum value - minimum value). For ordinal variables, the smallest ordinal value is set to 0, the larger ordinal value is set to 1, and the ordinal values in between are converted proportionally. In the case of categorical variables, each category value is usually treated as one variable, and a binomial value of 0 or 1 is used depending on the presence or absence of the category value. It is desirable to have a certain number of data for each category value, but if the number of data is small, it is sometimes combined with adjacent category values. Missing values are either removed or replaced by estimating a value appropriate for the data.
2) Number of input nodes
If the variable is binomial or continuous data, assign one input node to each variable. If the variable
is categorical, assign one input node to each categorical value.
3) Number of output nodes
If there are two groups, one output node is sufficient. If there are \(K\) groups, assign \(K\) output nodes.
4) Number of hidden layers and number of hidden nodes
Determining the number of hidden layers and number of hidden nodes is a problem of determining
the nonlinear function of the neural network model. If the number of hidden layers and hidden nodes increases,
the model may be overfitted, so if possible, it is good to have a model that can classify satisfactorily
with a small number of hidden layers and hidden nodes. However, there is no exact method to find
the optimal number of hidden layers and hidden nodes. Usually, after setting the number of hidden layers and
hidden nodes sufficiently, we reduce them one by one and select a model with high accuracy and
a small number of hidden layers and hidden nodes. At this time, model selection criteria such as
AIC (Akaike information criteria) can be used.
If possible, it is good to obtain the classification function by setting the number of hidden layers to 1.
However, if too many nodes are created in one hidden layer, the number of hidden layers is set to two,
and the number of nodes in each layer is reduced. It is usually done so that the number of nodes in each layer
does not exceed twice the number of nodes in the input layer. Experiments to determine the number of
hidden layers and nodes take the most time in artificial neural network models.
5) Selection of activation function
Among the activation functions in Table 7.4.2, the sigmoid function, which is useful for the estimation algorithm
of weight coefficients, is often used. The activation function is known to affect the algorithm speed
during the training process of a neural network but does not have a significant effect on the results.
6) Initial value problem
Algorithms that estimate the weight coefficients of a multilayer neural network model require initial values,
and most of them randomly generate values between -1 and 1. Since there is a possibility that a given initial value
will find a local solution, it is necessary to experiment several times to find the same weight coefficients
by trying various initial values.
7) Interpretation of output variables
If there are two groups and one output node, the output value is a continuous value, so it can be classified
based on an appropriate boundary value. If there are multiple groups, the number of output nodes is usually
the same as the number of groups, and the group is classified based on the value of the output node
that is large (or small).
8) Sensitivity analysis
After obtaining the solution of the neural network using training data, it is a good idea to conduct
sensitivity analysis to determine the relative importance of the input variables. Change the value of
the input variable from the minimum to the maximum and examine the change in the output value.
Learning algorithm of multilayer neural networks
Let the input node values of a multilayer neural network with \(m\) input variables be \(\boldsymbol x = (x_{1}, x_{2}, ... , x_{m})\). Let the weight coefficient connecting node \(j\) to node \(k\) in the neural network be \(w_{jk}\), the constant coefficient at this time be \(w_{0k}\), and let all the weight coefficients appearing in this neural network be \(\boldsymbol w\). The output of the neural network can be expressed as \(\hat y = f(\boldsymbol x : \boldsymbol w )\), where the function \(f\) is a composite function of several combination functions and activation functions as in Theorem 7.4.1. In order to find the weight coefficient \(\boldsymbol w\) of the multilayer neural network, it is reasonable to minimize the distance \(d(y_{i}, \hat y_{i})\) between the observed group value \(y_{i}\) of all data and the estimated value \(\hat y_{i}\) of the neural network. If we use the Euclidean square distance, we find the weight coefficient that minimizes the error sum of squares \(\small E(\boldsymbol w )\) as follows. $$ E(\boldsymbol w ) = \sum_{i=1}^{n} \; ( y_{i} - \hat y_{i} )^2 $$ To find \(\boldsymbol w\) that minimizes the error sum of squares, we differentiate \(\small E(\boldsymbol w )\) with respect to each \(w_{jk}\) as follows. $$ \frac{\partial E(\boldsymbol w )}{\partial w_{jk}} = -2 \sum_{i=1}^{n} \; ( y_{i} - \hat y_{i} ) \; \frac{\partial \hat y_{i}}{\partial w_{jk} } $$ If \(\hat y_{i}\) is estimated using the sigmoid activation function, the rate of change of the estimated value, \(\small \frac{\partial \hat y_{i}}{\partial w_{jk} }\), is proportional to \(\hat y_{i} (1 - \hat y_{i}) \) due to the differentiation characteristic of the sigmoid function. Therefore, we can create an algorithm to search for weight coefficients as follows. $$ w_{jk} \;←\; w_{jk} \;-\; \lambda \; \frac{\partial E(\boldsymbol w )}{\partial w_{jk} } $$ Here, \(\lambda\) is the learning rate, which has a value between 0 and 1. \(\frac{\partial E(\boldsymbol w )}{\partial w_{jk} }\) means the gradient descent rate, which implies that the estimation of weight coefficients should be adjusted in the direction that decreases the total error sum of squares. If the output value of input node \(j\) is \(O_{j}\) and the error at output node \(k\) is \(E_{k}\), the above update of weight coefficients is as follows. $$ w_{jk} \;←\; w_{jk} \;-\; \lambda \; E_{k} O_{j} $$ Here, \(\small \lambda \; E_{k} O_{j}\) is the change amount of the weight coefficient, which is the same concept as the estimation of the weight coefficient of the single-layer neural network. That is, the weight coefficient is updated as a learning rate \(\lambda\) proportional to the input \(O_{j}\) from node \(j\) by considering the error \(E_{k}\) of node \(k\). In a similar way, the bias constant \(w_{0k}\) is updated as follows. $$ w_{0k} \;←\; w_{0k} \;-\; \lambda \; E_{k} $$ In this algorithm, the estimation of \(E_{k}\) and \(O_{j}\) is not easy when applied to the hidden nodes in the multilayer neural network model, so the back-propagation algorithm developed by Hopefield is used. The back-propagation algorithm sets a criterion for optimizing the initial weight coefficients and the objective function, and divides it into the forward step and the backward step to repeatedly update the weight coefficients. In the forward step, the estimated weight coefficients are used to calculate the output values of all nodes, and the output values of the nodes in the layer \(l\) are used to calculate the output values of the nodes in the layer \(l+1\). In the backward step, the output values and error values for the nodes in the calculated layer \(l+1\) are used to estimate the error values for the nodes in the layer \(l\) and the weight coefficients are updated. This method is repeatedly applied until the weight coefficients hardly change or the objective function value is optimized, and the algorithm is stopped.
When the sigmoid activation function is used in the multilayer neural network in <Figure 7.4.5>, let us estimate the weight coefficients by applying the back-propagation algorithm. First, the initial weight coefficients are used to obtain the output values \(O_{1}, O_{2}, ..., O_{6}\) of each node. Here, \(O_{1}, O_{2}, O_{3}\) are the values of the input variable \(x_{1}, x_{2}, x_{3}\). The key is how to obtain the error \(E_{k}\) of each node. In the back-propagation algorithm, it is estimated by considering the weighted sum of the errors of all nodes connected to node \(k\). In the case of a sigmoid function, the rate of change \(\small \frac{\partial \hat y_{i}}{\partial w_{jk} }\) is proportional to \(\hat y_{i} (1 - \hat y_{i}) \), so the error \(E_{6}\) of the output node ⑥ is estimated as follows. $$ E_{6} \;=\; O_{6}(1-O_{6})(y_{i} - O_{6}) $$ Here, \(O_{6}(1-O_{6})\) denotes the rate of change \(\hat y_{i}(1 - \hat y_{i})\), and the \((y_{i}-O_{6})\) term denotes the estimation error \((y_{i} - \hat y_{i})\). That is, the meaning of the error \(E_{6}\) is the estimation error \((y_{i} - O_{6})\) multiplied by the error change rate \(O_{6}(1-O_{6})\). The error \(E_{5}\) of hidden node ⑤ is calculated by multiplying the error change rate \(O_{5}(1-O_{5})\) by the weighted sum of errors of all nodes connected to node ⑤, which is called the back-propagation of the error. That is, $$ E_{5} \;=\; O_{5}(1-O_{5}) \sum_{k} \; w_{5k} E_{k} $$ After calculating the error \(E_{4}\) of hidden node ④ in a similar way, the weight coefficients are updated. Let us look at the back-propagation algorithm for estimating the weight coefficient of a multilayer neural network through the following example.
For the multilayer neural network model in Figure 7.4.5, let the input data be group 1 and the variable values be (\(x_{1}, x_{2}, x_{3}\) ) = (1, 0, 1). Let us find the weight coefficient and bias of the model equation using the back-propagation algorithm of the gradient descent method. The same sigmoid function, f(x), is used for all activation functions, and the initial values of the weight coefficient and bias are set as follows using a random number between (-1,1). Let the learning rate be \(\lambda\) = 0.1.
| Table 7.4.4 Initial values of the weight coefficients for the multilayer neural network in Figure 7.4.5 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \(w_{14}\) | \(w_{15}\) | \(w_{24}\) | \(w_{25}\) | \(w_{34}\) | \(w_{35}\) | \(w_{46}\) | \(w_{56}\) | \(w_{04}\) | \(w_{05}\) | \(w_{06}\) |
| -0.51 | -0.99 | 0.35 | -0.45 | 0.39 | 0.19 | 0.27 | 0.71 | -0.75 | -0.09 | 0.18 |
Answer
The forward step of the back-propagation algorithm calculates the output values of all nodes using the given initial values. In the neural network of <Figure 7.4.5>, the output values \(O_{1}, O_{2}, O_{3}\) of nodes ①, ②, and ③ are the values of the input variables \(x_{1}, x_{2}, x_{3}\), and the output values of nodes ④, ⑤, and ⑥ are as follows, using the given initial weight coefficients. $$ \small \begin{align} O_{4} &= f( w_{14} x_{1} + w_{24} x_{2} + w_{34} x_{3} + w_{04} ) \\ &= f( -0.51 \times 1 \;+\; 0.35 \times 0 \;+\; 0.39 \times 1 \;-\; 0.75 \\ &= f(-0.87) = 0.2953 \\ O_{5} &= f( w_{15} x_{1} + w_{25} x_{2} + w_{35} x_{3} + w_{05} ) \\ &= f( -0.99 \times 1 \;-\; 0.45 \times 0 \;+\; 0.19 \times 1 \;-\; 0.09 \\ &= f(-0.89) = 0.2911 \\ O_{6} &= f( w_{46} O_{4} + w_{56} O_{6} + w_{06} ) \\ &= f( 0.27 \times 0.2953 \;+\; 0.71 \times 0.2911 \;+\; 0.18 \\ &= f(0.4664) = 0.6145 \\ \end{align} $$ The backward step of the back-propagation algorithm first estimates the error \(\small E_{6}\) of node ⑥, and then estimates the errors of nodes ④ and ⑤. The estimation of the error \(\small E_{6}\) of node ⑥ is as follows. $$ \small \begin{align} E_{6} \;&=\; O_{6}(1-O_{6})(y_{i} - O_{6}) \\ &=\; 0.6145 \times (1-0.6145) \times (1 - 0.6145) = 0.0913 \end{align} $$ Here, the \(\small O_{6}(1-O_{6})\) term is the rate of change from the differentiation of the sigmoid function and \(y\) is the actual group value. The meaning of the error \(\small E_{6}\) is the estimation error, \(\small y_{i} - O_{6}\), multiplied by the error change rate \(\small O_{6}(1-O_{6})\). The error \(\small E_{5}\) of hidden node ⑤ is calculated by multiplying the error change rate \(\small O_{5}(1-O_{5})\) by the error weighted sum of all nodes connected to node ⑤, which is called back-propagation of the error. That is, $$ E_{5} \;=\; O_{5}(1-O_{5}) \sum_{k} \; w_{5k} E_{k} $$ In this problem, since there is only node ⑥ connected to node ⑤, \(\small E_{5}\) is as follows. The error \(\small E_{4}\) of node ④ is also calculated in the same way. $$ \small \begin{align} E_{5} \;&=\; O_{5}(1-O_{5}) w_{56} E_{6}) \\ &=\; 0.2911 \times (1-0.2911) \times 0.71 \times 0.0913 = 0.0134 \\ E_{4} \;&=\; O_{4}(1-O_{4}) w_{46} E_{6}) \\ &=\; 0.2953 \times (1-0.2953) \times 0.27 \times 0.0913 = 0.0051 \\ \end{align} $$ Therefore, the updated weight coefficients and biases are as follows. $$ \small \begin{align} w_{46} \;&←\; w_{46} + \lambda E_{6} O_{4} \;=\; 0.27 + 0.1 \times 0.0913 \times 0.2953 \;=\; 0.2727 \\ w_{56} \;&←\; w_{56} + \lambda E_{6} O_{5} \;=\; 0.71 + 0.1 \times 0.0913 \times 0.2911 \;=\; 0.7127 \\ w_{14} \;&←\; w_{14} + \lambda E_{4} x_{1} \;=\; -0.51 + 0.1 \times 0.0051 \times 1 \;=\; -0.5095 \\ w_{15} \;&←\; w_{15} + \lambda E_{5} x_{1} \;=\; -0.99 + 0.1 \times 0.0134 \times 1 \;=\; -0.9887 \\ w_{24} \;&←\; w_{24} + \lambda E_{4} x_{2} \;=\; +0.35 + 0.1 \times 0.0051 \times 0 \;=\; 0.3500 \\ w_{25} \;&←\; w_{25} + \lambda E_{5} x_{2} \;=\; -0.99 + 0.1 \times 0.0134 \times 0 \;=\; -0.4500 \\ w_{34} \;&←\; w_{34} + \lambda E_{4} x_{3} \;=\; +0.39 + 0.1 \times 0.0051 \times 1 \;=\; 0.3905 \\ w_{35} \;&←\; w_{35} + \lambda E_{5} x_{3} \;=\; +0.19 + 0.1 \times 0.0134 \times 1 \;=\; 0.1913 \\ w_{04} \;&←\; w_{04} + \lambda E_{4} \;=\; -0.75 + 0.1 \times 0.0051 \;=\; -0.7495 \\ w_{05} \;&←\; w_{06} + \lambda E_{5} \;=\; -0.09 + 0.1 \times 0.0134 \;=\; -0.0887 \\ w_{06} \;&←\; w_{06} + \lambda E_{6} \;=\; +0.18 + 0.1 \times 0.0913 \;=\; 0.1891 \\ \end{align}\; $$
When the back-propagation algorithm is repeated as many times as the number of data, it is said that the ‘neural network has learned’, but if the neural network is complex, the global optimal solution of the objective function may not be obtained, but a local optimal solution may be obtained, so caution is required. In algorithms that handle nonlinear functions, the final solution may be a local optimal value or a global optimal value depending on the initial value, so experiments should be conducted repeatedly through trial and error. Usually, as an initial value, a random number is selected from a uniform distribution in a certain area, and after an experiment, the initial value that shows the best result is selected.
Deep learning
Characteristics of neural network models
7.4.3 R and Python practice - Neural network
R practice
[Colab]
| nnet {nnet} | Fit Neural Networks Fit single-hidden-layer neural network, possibly with skip-layer connections. |
|---|---|
|
## S3 method for class 'formula' nnet(formula, data, weights, ..., subset, na.action, contrasts = NULL) ## Default S3 method: nnet(x, y, weights, size, Wts, mask, linout = FALSE, entropy = FALSE, softmax = FALSE, censored = FALSE, skip = FALSE, rang = 0.7, decay = 0, maxit = 100, Hess = FALSE, trace = TRUE, MaxNWts = 1000, abstol = 1.0e-4, reltol = 1.0e-8, ...) |
|
| formula | A formula of the form class ~ x1 + x2 + ... |
| x | matrix or data frame of x values for examples. |
| y | matrix or data frame of target values for examples. |
| weights | (case) weights for each example – if missing defaults to 1. |
| size | number of units in the hidden layer. Can be zero if there are skip-layer units. |
| data | Data frame from which variables specified in formula are preferentially to be taken. |
| subset | An index vector specifying the cases to be used in the training sample. |
| na.action | A function to specify the action to be taken if NAs are found. The default action is for the procedure to fail. An alternative is na.omit, which leads to rejection of cases with missing values on any required variable. |
| contrasts | a list of contrasts to be used for some or all of the factors appearing as variables in the model formula. |
| Wts | initial parameter vector. If missing chosen at random. |
| mask | logical vector indicating which parameters should be optimized (default all). |
| linout | switch for linear output units. Default logistic output units. |
| entropy | switch for entropy (= maximum conditional likelihood) fitting. Default by least-squares. |
| softmax | switch for softmax (log-linear model) and maximum conditional likelihood fitting. linout, entropy, softmax and censored are mutually exclusive. |
| censored | A variant on softmax, in which non-zero targets mean possible classes. Thus for softmax a row of (0, 1, 1) means one example each of classes 2 and 3, but for censored it means one example whose class is only known to be 2 or 3. |
| skip | switch to add skip-layer connections from input to output. |
| rang | Initial random weights on [-rang, rang]. Value about 0.5 unless the inputs are large, in which case it should be chosen so that rang * max(|x|) is about 1. |
| decay | parameter for weight decay. Default 0. |
| maxit | maximum number of iterations. Default 100. |
| Hess | If true, the Hessian of the measure of fit at the best set of weights found is returned as component Hessian. |
| trace | switch for tracing optimization. Default TRUE. |
| MaxNWts | The maximum allowable number of weights. There is no intrinsic limit in the code, but increasing MaxNWts will probably allow fits that are very slow and time-consuming. |
| abstol | Stop if the fit criterion falls below abstol, indicating an essentially perfect fit. |
| reltol | Stop if the optimizer is unable to reduce the fit criterion by a factor of at least 1 - reltol. |
An example of R commands for the single-layer neural network model using the data as in Example 7.4.2 is as follows.
| install.packages('nnet') |
| library(nnet) |
| singleNNdata <- read.csv('http://estat.me/estat/Example/DataScience/SingleNN.csv', header=T, as.is=FALSE) |
| attach(signleNNdata) |
singleNNdata
x1 x2 x3 y 1 0 0 0 -1 2 0 0 1 -1 3 0 1 0 -1 4 0 1 1 1 5 1 0 0 -1 6 1 0 1 1 7 1 1 0 1 8 1 1 1 1 |
| # create a training data using the 8 data. train <- singleNNdata[1:8,] |
| # create a testing data using the same 8 data test <- singleNNdata[1:8,] |
train.nnet <- nnet(y~x1+x2+x3,data=train, size=2, rang=0.1, decay=5e-4, maxit=100)
# weights: 11 initial value 10.068006 iter 10 value 7.626637 iter 20 value 4.217955 iter 30 value 4.133499 iter 40 value 4.129743 iter 50 value 4.129625 iter 60 value 4.129609 iter 70 value 4.129607 iter 80 value 4.129601 final value 4.129595 converged |
summary(train.nnet)
a 3-2-1 network with 11 weights options were - decay=5e-04 b->h1 i1->h1 i2->h1 i3->h1 4.14 -3.06 -3.06 -3.06 b->h2 i1->h2 i2->h2 i3->h2 4.05 -3.01 -3.01 -3.01 b->o h1->o h2->o 4.63 -7.37 -7.17 |
In the summary, 3-2-1 network implies that there are 3 input layers (i1, i2, i3) - 2 hidden layers (h1, h2) - 1 output layer (o). There are 11 weights and b->h1 implies the bias constant to the hidden layer h1 which is 4.14. i1->h1 implies the weight coefficient from input layer i1 to the hidden layer h1 which is -3.06 etc. Therefore, the linear combination function to h1 is 4.14 - 3.06 × i1 - 3.06 × i2 - 3.06 × i3, the linear combination function to h2 is 4.05 - 3.01 × i1 - 3.01 × i2 - 3.01 × i3, and the linear combination function to o is 4.63 - 7.37 × h1 - 7.17 × h2.
The R command to classify the groups by testing all 8 data using the above model is as follows. First, if we classify the test data using the predict command with default activation function, the result will be a number.
predict(train.nnet,test)
[,1]
1 0.0000619568
2 0.0020718984
3 0.0020859221
4 0.9453979298
5 0.0020719570
6 0.9452023418
7 0.9453977511
8 0.9893836166
|
| nnetpred <- (predict(train.nnet,test) >= 0.01) |
table(nnetpred,y)
y
nnetpred -1 1
FALSE 4 0
TRUE 0 4
|
Python practice
[Colab]
|
# Import required libraries import pandas as pd import numpy as np from sklearn.neural_network import MLPClassifier # Load data singleNNdata = pd.read_csv('https://raw.githubusercontent.com/ogut77/DataScience/refs/heads/main/singleNN.csv') # Create training and testing data using the first 8 rows train = singleNNdata.iloc[:8] test = singleNNdata.iloc[:8] # Prepare features and target for training X_train = train[['x1', 'x2', 'x3']] y_train = train['y'] # Initialize and train the neural network # size=2 (2 hidden neurons), decay=5e-4 (weight decay), maxit=100 (max iterations) nn_model = MLPClassifier(hidden_layer_sizes=(2,), alpha=5e-4, max_iter=100, random_state=0, learning_rate_init=0.1) # rang=0.1 maps to initial learning rate nn_model.fit(X_train, y_train) # Print model summary print("Number of layers:", nn_model.n_layers_) print("Number of neurons in hidden layer:", nn_model.hidden_layer_sizes) print("Output layer activation:", nn_model.out_activation_) print("Loss:", nn_model.loss_) print("Number of iterations:", nn_model.n_iter_) print("Weights:", nn_model.coefs_) print("Biases:", nn_model.intercepts_) # Neural Network - Predictions and Confusion Matrix y_pred_nn = nn_model.predict(X_test) y_pred_prob = nn_model.predict_proba(X_test) accuracy_nn = accuracy_score(y_test, y_pred_nn) cm_nn = confusion_matrix(y_test, y_pred_nn) print(f"Neural Network Probability Prediction:\n {y_pred_prob}") print(f"Neural Network Accuracy: {accuracy_nn}") print(f"Neural Network Confusion Matrix:\n{cm_nn}") |
7.5 Support vector machine model
7.5.1 Linear support vector machine
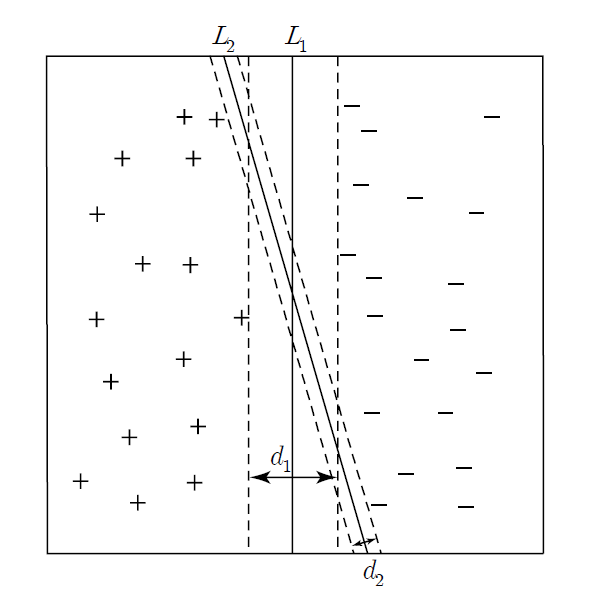
The distance \(d_{1}\) of \(L_{1}\) is larger than \(d_{2}\) of \(L_{2}\), so \(L_{1}\) has less possibility of misclassification.
Linear SVM can be explained by dividing the data of two groups into cases where they can be linearly separable using a linear classification function as shown in <Figure 7.5.1> and cases where they cannot be linearly separable.
A. Linearly separable case
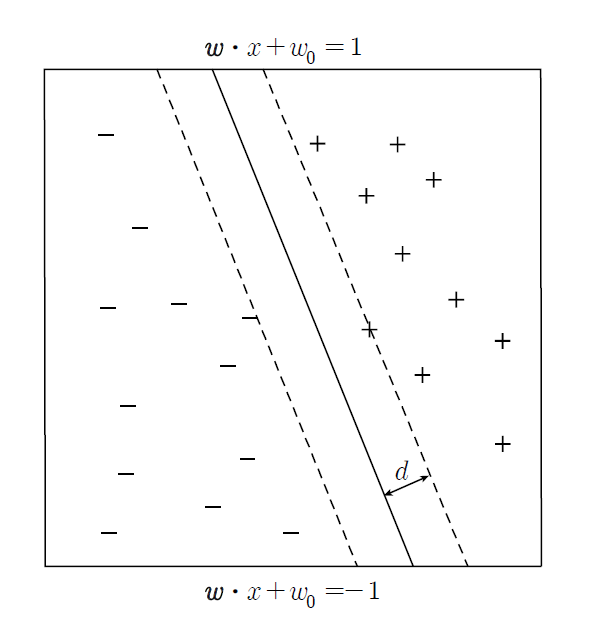
The hyperplane that maximizes the distance (margin \(d\)) is likely to have less misclassification in actual classification.
If \(\boldsymbol x_{1}\) lies in the hyperplane \(\boldsymbol w \;\cdot\; \boldsymbol x_{i} \;+\; w_{0} \;=\; 1\), then \(\boldsymbol w \;\cdot\; \boldsymbol x_{1} \;+\; w_{0} \;=\; 1\), and if \(\boldsymbol x_{2}\) lies in the hyperplane \(\boldsymbol w \;\cdot\; \boldsymbol x_{i} \;+\; w_{0} \;=\; -1\), then \(\boldsymbol w \;\cdot\; \boldsymbol x_{2} \;+\; w_{0} \;=\; -1\). Therefore, we have the followings. $$ \boldsymbol w \;\cdot\; ( \boldsymbol x_{1} \;-\; \boldsymbol x_{2}) \;=\; 2 $$
When there are eight data for two variables \(x_{1}\) (age), \(x_{2}\) (monthly income) and group variable \(y\) (+1: purchase, -1: non-purchase) as in Table 7.5.1, find the classification equation using a linear support vector model.
| Table 7.5.1 Eight data with two variables and their group | |||
|---|---|---|---|
number |
Age \(x_{1}\) |
Income \(x_{2}\) |
Group \(y\) |
| 1 | 25 | 150 | -1 |
| 2 | 34 | 220 | +1 |
| 3 | 26 | 210 | -1 |
| 4 | 28 | 250 | +1 |
| 5 | 21 | 100 | -1 |
| 6 | 31 | 220 | +1 |
| 7 | 36 | 300 | +1 |
| 8 | 20 | 100 | -1 |
Answer
If we draw a scatter plot for the data in Table 7.5.1, it is a case where linear separation is possible as in <Figure 7.5.3>. In the figure, o means + group and r means - group, and we can see that there are many straight lines that can classify the two groups.
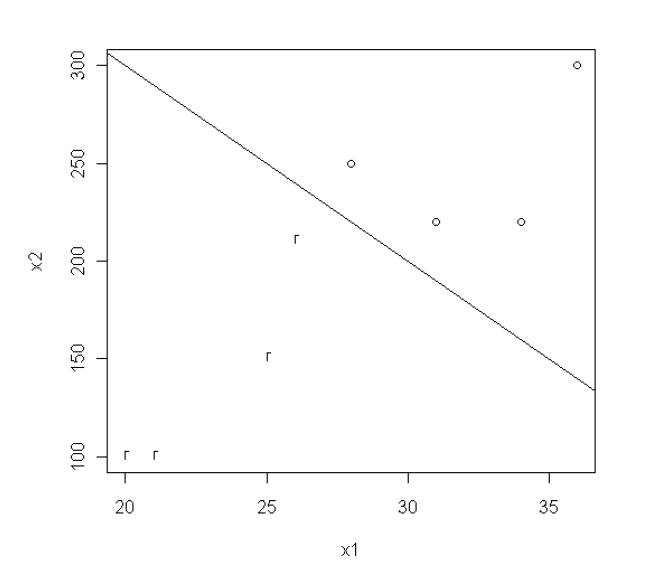
If we find the solution to the quadratic programming of the linear support vector, the classification function is 0.333 \(x_{1}\) + 0.033 \(x_{2}\) - 16.667 = 0 which is the line in <Figure 7.5.3> Therefore, the decision rule is as follows. $$ \small \text{If} \;\; 0.333 x_{1} + 0.033x_{2} - 16.667 \;≥\; 0, \;\; \text{classify}\; '+1' \; \text{group, else}\; '-1' \text{group}. $$
B. Linearly not separable case
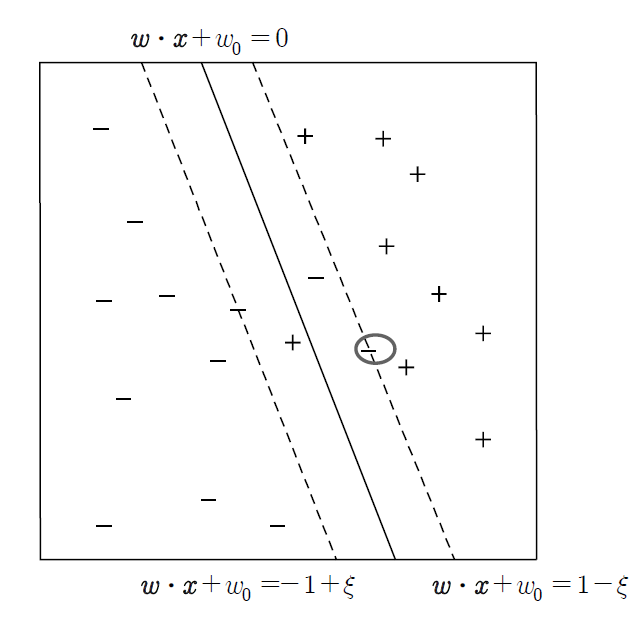
In <Figure 7.5.4>, the slack variable \(\xi\) means that the hyperplane (\( \boldsymbol w \;\cdot\; \boldsymbol x \;+\; w_{0} = -1 \)) where linear classification is possible has moved parallel to the hyperplane \( \boldsymbol w \;\cdot\; \boldsymbol x \;+\; w_{0} = -1 + \xi \) that can include the data of the - group, which is indicated by a circle. The distance between these two hyperplanes can be shown to be \(\frac{\xi}{|| \boldsymbol w ||}\), and the nonlinear optimization problem to minimize misclassification in the case of linearly non-separable is as follows. $$ \begin{multline} \shoveleft \qquad \text{Find} \;\; \boldsymbol w, w_{0}, \xi_{i} \;\text{which} \;\; \text{minimize} \frac{|| \boldsymbol w ||^2}{2^2} + C(\sum_{i=1}^{n} \; \xi_{i} )^k \\ \shoveleft \qquad \text{subject to} \\ \shoveleft \qquad y_{i} \;( \boldsymbol w \;\cdot\; \boldsymbol x_{i} \;+\; w_{0}) \;≥\; 1 - \xi_{i}, \;\; i=1,2,...,n \end{multline} $$ Here, the function \(C(x)\) is a penalty function that minimizes the slack variable, which means an error, and \(C(x)\) and \(k\) can be selected arbitrarily by the user. This nonlinear optimization problem can also be solved by the Lagrangian multiplier method, but the details are beyond the level of this book, so we will omit them.
In this section, we introduce the SVM model for the case of two groups, but it can be extended to the case of multiple groups.
7.5.2 Nonlinear support vector machine
Characteristics of the support vector machine model
7.5.3 R and Python practice - Support vector machine
R practice
[Colab]
| svm {e1071} | Fit support vector machine |
|---|---|
|
# S3 method for formula, svm(formula, data = NULL, ..., subset, na.action =na.omit, scale = TRUE) # S3 method for default svm(x, y = NULL, scale = TRUE, type = NULL, kernel = "radial", degree = 3, gamma = if (is.vector(x)) 1 else 1 / ncol(x), coef0 = 0, cost = 1, nu = 0.5, class.weights = NULL, cachesize = 40, tolerance = 0.001, epsilon = 0.1, shrinking = TRUE, cross = 0, probability = FALSE, fitted = TRUE, ..., subset, na.action = na.omit) |
|
| formula | A formula of the form class ~ x1 + x2 + ... |
| data | an optional data frame containing the variables in the model. By default the variables are taken from the environment which ‘svm’ is called from. |
| x | a data matrix, a vector, or a sparse matrix (object of class Matrix provided by the Matrix package, or of class matrix.csr provided by the SparseM package, or of class simple_triplet_matrix provided by the slam package). |
| y | a response vector with one label for each row/component of x. Can be either a factor (for classification tasks) or a numeric vector (for regression). |
| scale | A logical vector indicating the variables to be scaled. If scale is of length 1, the value is recycled as many times as needed. Per default, data are scaled internally (both x and y variables) to zero mean and unit variance. The center and scale values are returned and used for later predictions. |
| type |
svm can be used as a classification machine, as a regression machine, or for novelty detection. Depending of whether y is a factor or not, the default setting for type is C-classification or eps-regression, respectively, but may be overwritten by setting an explicit value. Valid options are: C-classification nu-classification one-classification (for novelty detection) eps-regression nu-regression |
| kernel | the kernel used in training and predicting. We might consider changing some of the following parameters, depending on the kernel type. linear: polynomial: radial basis: sigmoid: |
| degree | parameter needed for kernel of type polynomial (default: 3) |
| gamma | parameter needed for all kernels except linear (default: 1/(data dimension)) |
| coef0 | parameter needed for kernels of type polynomial and sigmoid (default: 0) |
| cost | cost of constraints violation (default: 1)---it is the ‘C’-constant of the regularization term in the Lagrange formulation |
| nu | parameter needed for nu-classification, nu-regression, and one-classification |
| class.weights | a named vector of weights for the different classes, used for asymmetric class sizes. Not all factor levels have to be supplied (default weight: 1). All components have to be named. Specifying "inverse" will choose the weights inversely proportional to the class distribution. |
| cachesize | cache memory in MB (default 40) |
| tolerance | tolerance of termination criterion (default: 0.001) |
| epsilon | epsilon in the insensitive-loss function (default: 0.1) |
| shrinking | option whether to use the shrinking-heuristics (default: TRUE) |
| cross | if a integer value k>0 is specified, a k-fold cross validation on the training data is performed to assess the quality of the model: the accuracy rate for classification and the Mean Squared Error for regression |
| fitted | logical indicating whether the fitted values should be computed and included in the model or not (default: TRUE) |
| probability | logical indicating whether the model should allow for probability predictions. |
| subset | An index vector specifying the cases to be used in the training sample. (NOTE: If given, this argument must be named.) |
| na.action | A function to specify the action to be taken if NAs are found. The default action is na.omit, which leads to rejection of cases with missing values on any required variable. An alternative is na.fail, which causes an error if NA cases are found. (NOTE: If given, this argument must be named.) |
An example of R commands for the single-layer neural network model using the data as in Example 7.4.2 is as follows.
| install.packages('e1071') |
| library(e1071) |
| svmdata <- read.csv('http://estat.me/estat/Example/DataScience/Svmdata.csv', header=T, as.is=FALSE) |
| attach(svmdata) |
svmdata
x1 x2 y 1 25 150 -1 2 34 220 1 3 26 210 -1 4 28 250 1 5 21 100 -1 6 31 220 1 7 36 300 1 8 20 100 -1 |
| # create a training data using the 8 data. train <- svmdata[1:8,] |
| # create a testing data using the same 8 data test <- svmdata[1:8,] |
| train.svm = svm(y~x1+x2,type="C-classification", data=train) |
train.svm
Call:
svm(formula = y ~ x1 + x2, data = train, type = "C-classification")
Parameters:
SVM-Type: C-classification
SVM-Kernel: radial
cost: 1
Number of Support Vectors: 6
|
The R command to reclassify the entire 8 data into groups using the above model is as follows. Classifying the test data shows that all data are classified correctly.
| svmpred = predict(train.svm,test) > svmpred 1 2 3 4 5 6 7 8 -1 1 -1 1 -1 1 1 -1 Levels: -1 1 |
| z = table(svmpred,y) |
z
y
svmpred -1 1
-1 4 0
1 0 4
|
The R command to draw a scatter plot of x1, x2, labeled with the values of y, and a classification line 500 - 10 x1 on the scatter plot is as follows.
| plot(x1,x2,pch=y) |
abline(500,-10)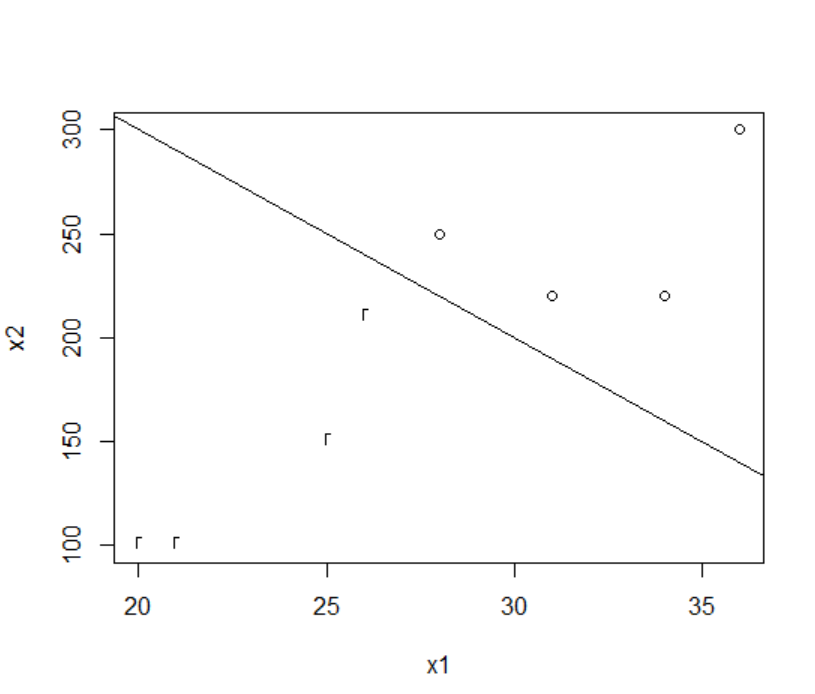
|
Python practice
[Colab]
|
# Import required libraries import pandas as pd import numpy as np from sklearn.svm import SVC import matplotlib.pyplot as plt # Load data svmdata = pd.read_csv('https://raw.githubusercontent.com/ogut77/DataScience/refs/heads/main/svmdata.csv') # Create training and testing data using the first 8 rows train = svmdata.iloc[:8] test = svmdata.iloc[:8] # Prepare features and target for training X_train = train[['x1', 'x2']] y_train = train['y'] X_test = test[['x1', 'x2']] y_test = test['y'] # Train SVM model (C-classification) svm_model = SVC(kernel='linear') # R's svm with type="C-classification" defaults to linear kernel svm_model.fit(X_train, y_train) # Print model details print("Support Vectors:", svm_model.support_vectors_) print("Number of Support Vectors:", svm_model.n_support_) # Predict on test data svm_pred = svm_model.predict(X_test) print("Predictions:", svm_pred) # Create confusion matrix z = pd.crosstab(svm_pred, y_test, rownames=['Predicted'], colnames=['Actual']) print("Confusion Matrix:\n", z) # Plot data points with class labels plt.scatter(X_train['x1'], X_train['x2'], c=y_train, cmap='bwr', marker='o') plt.xlabel('x1') plt.ylabel('x2') # Plot the line abline(500, -10), which in Python is y = 500 - 10x x = np.linspace(min(X_train['x1']), max(X_train['x1']), 100) y = 500 - 10 * x plt.plot(x, y, 'k-') plt.show() Support Vectors: [[ 26. 210.] [ 31. 220.]] Number of Support Vectors: [1 1] Predictions: [-1 1 -1 1 -1 1 1 -1] Confusion Matrix: Actual -1 1 Predicted -1 4 0 1 0 4 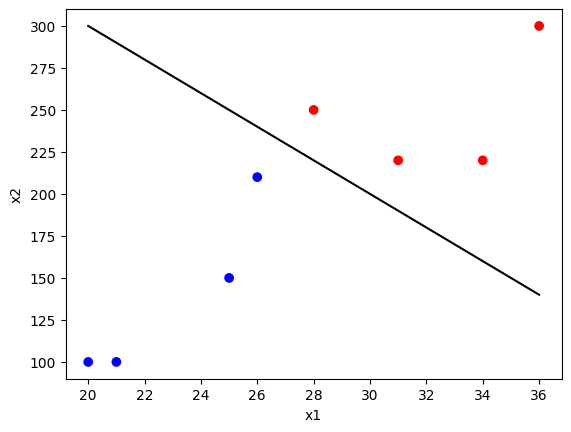
|
7.6 Ensemble model
The ensemble model can obtain better classification results than a single classifier. For example, suppose five classifiers classify two groups, and each has a misclassification rate of 5%. If the five classifiers are independent models, the ensemble model will misclassify if more than half of the classifiers are misclassified. In other words, the misclassification rate \(e_{ensemble}\) of the ensemble model is as follows. $$ e_{ensemble} \;=\; \sum_{i=3}^{5} \; {}_{5} C_{i} \; (0.05)^i (1-0.05)^{5-i} \;=\; 0.0001 $$ Therefore, the misclassification rate of the ensemble model is smaller than that of each classifier. For the ensemble model to have better classification results than each classifier, each classifier must be independent, and the misclassification rate must be at least less than 50%. In practice, it is often difficult to say that each classifier is completely independent, but even in such cases, the classification results of the ensemble model are known to be good.
Each classifier used in the ensemble model can be any classification model. However, while applying one model, we can create multiple classifiers by adjusting the data, adjusting the number of variables, or adjusting the group name.
A. Adjust the number of data
B. Control the number of variables
C. Control group names
D. Adjust classification model assumptions
7.6.1 Bagging
| Step 1 | Let \(R\) be the number of bootstrap samples, and \(n\) be the sample size |
| Step 2 | for k = 1 to R do |
| Step 3 | \(\qquad\)Generate bootstrap samples \(D_{k}\) of size \(n\) |
| Step 4 | \(\qquad\)Create classifier \(C_{k}\) using bootstrap samples \(D_{k}\) |
| Step 5 | end for |
| Step 6 | Classify an unknown data \(\boldsymbol x\) into the majority vote of all classifiers, that is, $$C^{*} (\boldsymbol x ) = {argmax}_{y} \; \sum_{k=1}^{R} \; I(C_{k} (\boldsymbol x) = y ) $$ |
A survey of 10 people who visited a store showed monthly income \(x\) and purchasing status \(y\) (purchasers have a value of 1 and non-purchasers have a value of -1), as shown in Table 7.6.1. We want to use a simple decision tree classifier such that ‘If \(x ≤ c\), classify \(x\) into purchaser group 1, otherwise classify into non-purchaser group -1’. This is called a decision stump, and \(c\) is determined so that the entropy is minimized (see Section 6.2). Classify this data using the bagging method.
| Table 7.6.1 Ten customer data with income \(x\) and purchase status \(y\) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \(x\) | 100 | 120 | 160 | 180 | 186 | 190 | 210 | 250 | 270 | 300 |
| \(y\) | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 |
Answer
In the above data, the branching that minimizes entropy is \(c\) = 170 or 200 (see Section 6.2). In both cases, the classification accuracy is 70%. Table 7.6.2 shows ten bootstrap samples and their classifiers that minimize entropy for applying the bagging method.
| Table 7.6.2 Ten bootstrap samples and each classifier | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| number | Bootstrap sample | Classifier | ||||||||||
| Sample 1 | \(x\) | 100 | 120 | 120 | 160 | 180 | 180 | 186 | 190 | 270 | 270 | If \(x ≤ 170\), then \(y\) = 1, else \(y\) = -1 |
| \(y\) | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | ||
| Sample 2 | \(x\) | 100 | 120 | 160 | 180 | 186 | 250 | 270 | 300 | 300 | 300 | If \(x ≤ 300\), then \(y\) = 1, else \(y\) = -1 |
| \(y\) | 1 | 1 | 1 | -1 | -1 | 1 | 1 | 1 | 1 | 1 | ||
| Sample 3 | \(x\) | 100 | 120 | 160 | 180 | 180 | 186 | 210 | 210 | 250 | 270 | If \(x ≤ 170\), then \(y\) = 1, else \(y\) = -1 |
| \(y\) | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | ||
| Sample 4 | \(x\) | 100 | 100 | 120 | 180 | 180 | 186 | 186 | 210 | 250 | 270 | If \(x ≤ 150\), then \(y\) = 1, else \(y\) = -1 |
| \(y\) | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | ||
| Sample 5 | \(x\) | 100 | 100 | 120 | 186 | 190 | 190 | 190 | 300 | 300 | 300 | If \(x ≤ 153\), then \(y\) = 1, else \(y\) = -1 |
| \(y\) | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | ||
| Sample 6 | \(x\) | 120 | 180 | 186 | 190 | 210 | 210 | 210 | 250 | 270 | 300 | If \(x ≤ 230\), then \(y\) = -1, else \(y\) = 1 |
| \(y\) | 1 | -1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | ||
| Sample 7 | \(x\) | 100 | 180 | 180 | 190 | 210 | 250 | 270 | 270 | 270 | 300 | If \(x ≤ 230\), then \(y\) = -1, else \(y\) = 1 |
| \(y\) | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 | 1 | ||
| Sample 8 | \(x\) | 100 | 120 | 186 | 186 | 186 | 210 | 210 | 250 | 270 | 300 | If \(x ≤ 230\), then \(y\) = -1, else \(y\) = 1 |
| \(y\) | 1 | 1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | ||
| Sample 9 | \(x\) | 100 | 160 | 180 | 180 | 190 | 210 | 210 | 250 | 300 | 300 | If \(x ≤ 230\), then \(y\) = -1, else \(y\) = 1 |
| \(y\) | 1 | 1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | ||
| Sample 10 | \(x\) | 100 | 100 | 100 | 100 | 160 | 160 | 250 | 250 | 270 | 270 | If \(x ≤ 50\), then \(y\) = -1, else \(y\) = 1 |
| \(y\) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
Table 7.6.3 shows the final classification results by majority vote after classifying the original 10 data by classifiers obtained from each sample. we can obtain the final classification results using a majority vote by adding the classified group of each classifier and examining the sign. The ensemble classification results by bagging accurately classify all data.
| Table 7.6.3 Classification results of each data by bagging 10 classifier | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Classifier of each sample | Income data \(x\) | |||||||||||
| 100 | 120 | 160 | 180 | 186 | 190 | 210 | 250 | 270 | 300 | |||
| Classifier 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | ||
| Classifier 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| Classifier 3 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | ||
| Classifier 4 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | ||
| Classifier 5 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | ||
| Classifier 6 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | ||
| Classifier 7 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | ||
| Classifier 8 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | ||
| Classifier 9 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | ||
| Classifier 10 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| Total | 2 | 2 | 2 | -6 | -6 | -6 | -6 | 2 | 2 | 2 | ||
| Sign of Total | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | ||
| Actual group \(y\) | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | ||
7.6.2 R and Python practice - Bagging
R practice
[Colab]
| bagging {adabag} | Applies the Bagging algorithm to a data set Fits the Bagging algorithm proposed by Breiman in 1996 using classification trees as single classifiers. |
|---|---|
| bagging(formula, data, mfinal = 100, control, par=FALSE,...) | |
| formula | a formula, as in the lm function. |
| data | a data frame in which to interpret the variables named in the formula |
| mfinal | an integer, the number of iterations for which boosting is run or the number of trees to use. Defaults to mfinal=100 iterations. |
| control | options that control details of the rpart algorithm. See rpart.control for more details. |
| par | if TRUE, the cross validation process is runned in parallel. If FALSE (by default), the function runs without parallelization. |
| Details: Unlike boosting, individual classifiers are independent among them in bagging | |
| Value: An object of class bagging, which is a list with the following components: | |
| formula | the formula used. |
| trees | the trees grown along the iterations. |
| votes | a matrix describing, for each observation, the number of trees that assigned it to each class. |
| prob | a matrix describing, for each observation, the posterior probability or degree of support of each class. These probabilities are calculated using the proportion of votes in the final ensemble. |
| class | the class predicted by the ensemble classifier. |
| samples | the bootstrap samples used along the iterations. |
| importance | returns the relative importance of each variable in the classification task. This measure takes into account the gain of the Gini index given by a variable in each tree. |
An example of R commands for the bagging ensemble model using the iris data stored in R is as follows.
| install.packages('adabag') |
| library(adabag) |
| data(iris) |
| # mfinal is an integer which is the number of iterations for which boosting is run iris.bagging <- bagging(Species~., data=iris, mfinal = 10)) |
| # list the importance of variable in the classification iris.bagging$importance
Petal.Length Petal.Width Sepal.Length Sepal.Width
79.46481 20.53519 0.00000 0.00000
|
| # list the trees grown along the iterations. iris.bagging$trees
[[1]]
n= 150
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 150 94 virginica (0.32666667 0.30000000 0.37333333)
2) Petal.Length< 2.45 49 0 setosa (1.00000000 0.00000000 0.00000000) *
3) Petal.Length>=2.45 101 45 virginica (0.00000000 0.44554455 0.55445545)
6) Petal.Width< 1.75 49 4 versicolor (0.00000000 0.91836735 0.08163265)
12) Petal.Length< 4.95 42 0 versicolor (0.00000000 1.00000000 0.00000000) *
13) Petal.Length>=4.95 7 3 virginica (0.00000000 0.42857143 0.57142857) *
7) Petal.Width>=1.75 52 0 virginica (0.00000000 0.00000000 1.00000000) *
...
...
...
[[10]]
n= 150
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 150 92 setosa (0.38666667 0.34666667 0.26666667)
2) Petal.Length< 2.6 58 0 setosa (1.00000000 0.00000000 0.00000000) *
3) Petal.Length>=2.6 92 40 versicolor (0.00000000 0.56521739 0.43478261)
6) Petal.Length< 4.75 46 1 versicolor (0.00000000 0.97826087 0.02173913) *
7) Petal.Length>=4.75 46 7 virginica (0.00000000 0.15217391 0.84782609) *
|
| # plot the decision tree after iteration 10 data plot(iris.bagging$trees[[10]]) |
text(iris.bagging$trees[[10]])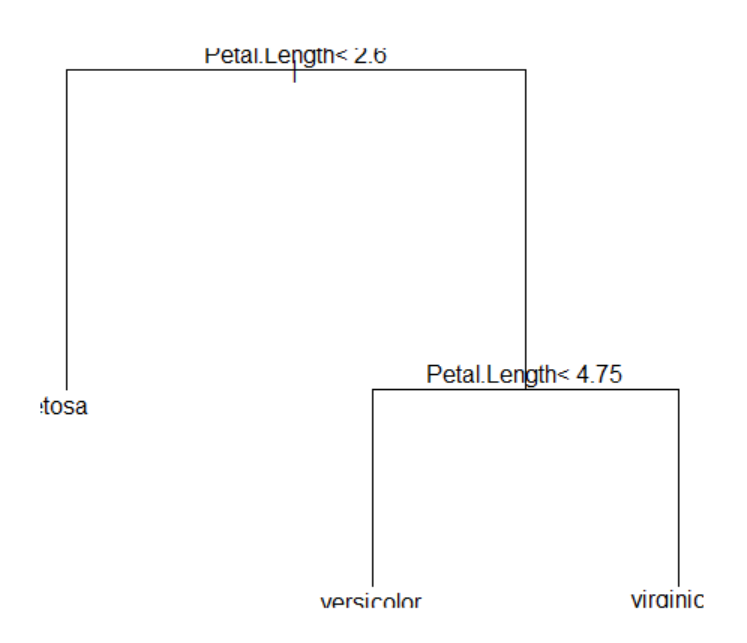
|
The R command to reclassify the entire iris data using the bagging model is as follows.
| # classify the iris data using the bagging model baggingpred <- predict(iris.bagging, newdata=iris) |
table(baggingpred$class, iris[,5])
setosa versicolor virginica
setosa 50 0 0
versicolor 0 47 1
virginica 0 3 49
|
| # calculate the misclassification error baggingtb <- table(baggingpred$class, iris[,5]) |
| baggingerror.rpart <- 1-(sum(diag(baggingtb))/sum(baggingtb)) |
| # misclassification error is 2.67% baggingerror.rpart [1] 0.02666667 |
Python practice
[Colab]
|
# Import required libraries import pandas as pd import numpy as np from sklearn.ensemble import AdaBoostClassifier from sklearn.tree import DecisionTreeClassifier, plot_tree from sklearn.metrics import confusion_matrix import matplotlib.pyplot as plt from sklearn.datasets import load_iris # Load iris dataset iris = load_iris() iris_df = pd.DataFrame(data=iris.data, columns=iris.feature_names) iris_df['Species'] = iris.target species_map = {0: 'setosa', 1: 'versicolor', 2: 'virginica'} iris_df['Species'] = iris_df['Species'].map(species_map) # Bagging with decision trees (mfinal=10 iterations) bagging_model = AdaBoostClassifier(n_estimators=10, random_state=0) X = iris_df.drop('Species', axis=1) y = iris_df['Species'] bagging_model.fit(X, y) # Feature importance importance = bagging_model.feature_importances_ feature_names = iris.feature_names importance_df = pd.Series(importance, index=feature_names) print("Feature Importance:\n", importance_df) # List of trees (equivalent to iris.bagging$trees) trees = bagging_model.estimators_ print("Number of trees:", len(trees)) # Plot the decision tree for the 10th iteration plt.figure(figsize=(10, 6)) plot_tree(trees[9], feature_names=feature_names, class_names=list(species_map.values()), filled=True) plt.title("Decision Tree for Iteration 10") plt.show() # Predict on the iris dataset bagging_pred = bagging_model.predict(X) # Confusion matrix conf_matrix = confusion_matrix(y, bagging_pred, labels=['setosa', 'versicolor', 'virginica']) conf_matrix_df = pd.DataFrame(conf_matrix, index=['setosa', 'versicolor', 'virginica'], columns=['setosa', 'versicolor', 'virginica']) print("Confusion Matrix:\n", conf_matrix_df) # Calculate misclassification error bagging_error = 1 - (np.diag(conf_matrix).sum() / conf_matrix.sum()) print("Misclassification Error:", bagging_error) print("Misclassification Error (%):", bagging_error * 100, "%") Feature Importance: sepal length (cm) 0.000000 sepal width (cm) 0.000000 petal length (cm) 0.599859 petal width (cm) 0.400141 dtype: float64 Number of trees: 10 
Confusion Matrix:
setosa versicolor virginica
setosa 50 0 0
versicolor 0 47 3
virginica 0 2 48
Misclassification Error: 0.033333333333333326
Misclassification Error (%): 3.3333333333333326 %
|
7.6.3 Boosting
When there are \(n\) training data, the boosting method first gives each data an equal probability of being selected as \(\frac{1}{n}\), just like bagging, and then extracts \(n\) bootstrap data with replacement. After creating a classifier using this bootstrap data, the original training data is classified by this classifier, either as a correct classification or a misclassification. If the data is misclassified, the probability of this data being selected is increased, so it is more likely to be selected in the next stage, and if the data is correctly classified, the probability of being selected in the next stage is decreased. Since the data that was not extracted is also likely to be misclassified, the probability of being selected is also increased. If this method is used repeatedly, data that is continuously misclassified will be more focused.
Recently, many types of research on boosting algorithms have been studied, and the algorithms differ depending on (1) ‘How do we modify the probability of extracting data in each boosting round?’ and (2) ‘How do we synthesize the classifiers determined in each boosting round to make the final classification?’. We introduce the widely used adaptive boosting algorithm called AdaBoosting.
AdaBoosting algorithm
The method of synthesizing the classification results of the \(R\) classifiers generated for the data \(\boldsymbol x \) of which the group is unknown does not use majority voting, but uses the result of weighting each classification result by the importance \(\alpha_{k}\). $$ C^{*} (\boldsymbol x ) = {argmax}_{v} \; \sum_{k=1}^{R} \; \alpha_{k} \; I(C_{k} (\boldsymbol x) = v ) $$ The Adaboosting algorithm that synthesizes the above explanations is as follows.
| Step 1 | Let \( D = \{(\boldsymbol x_{1}, y_{1}), (\boldsymbol x_{2}, y_{2}), ... , (\boldsymbol x_{n}, y_{n}) \}\) be the set of training data |
| Step 2 | Let the initial probability being selected be \( p_{i}^{(1)} = \frac{1}{n}, i=1,2, ... , n\). |
| Step 3 | Let \(R\) be the number of bootstrap samples. |
| Step 4 | for k = 1 to Rdo |
| Step 5 | \(\qquad\)Generate bootstrap samples \(D_{k}\) of size \(n\) using \( p_{i}^{(k)}\) |
| Step 6 | \(\qquad\)Create classifier \(C_{k}\) using bootstrap samples \(D_{k}\) |
| Step 7 | \(\qquad\)Apply \(C_{k}\) to each data of \(D\) whether it classifies correctly or not |
| Step 8 | \(\qquad\)calculates the misclassification rate \( \epsilon_{k} \;=\; \frac{1}{n} \; \left [ \; \sum_{i=1}^{n} \; p_{i} \; I \{ C_{k} (\boldsymbol x_{i}) \;\ne\; y_{i} \} \right ] \) |
| Step 9 | \(\qquad\)If \(\epsilon_{k} > 0.5\) then |
| Step 10 | \(\qquad \quad\)Set again initial probability \( p_{i}^{(1)} = \frac{1}{n}, i=1,2, ... , n\) |
| Step 11 | \(\qquad \quad\)Go back to Step 4 |
| Step 12 | \(\qquad\)end if |
| Step 13 | \(\qquad\)\(\alpha_{k} \;=\; \frac{1}{2} \; ln \; \frac{1- \epsilon_{k}}{\epsilon_{k}}\) |
| Step 14 | \(\qquad\)
\(
\begin{align}
p_{i}^{(k+1)} \;&=\; \frac {p_{i}^{(k)}}{Z_{k}} \times e^{-\alpha_{k}} \quad if \; C_{k} (\boldsymbol x_{i}) \;=\; y_{i} \\
\;&=\; \frac {p_{i}^{(k)}}{Z_{k}} \times e^{\alpha_{k}} \quad if \; C_{k} (\boldsymbol x_{i}) \;\ne\; y_{i} \\
\end{align}
\)
\(\qquad Z\) is a constant that makes the sum of probability becomes 1. |
| Step 15 | end for |
| Step 16 | Classify an unknown data \(\boldsymbol x\) into the weighted majority vote of each classifier, \( C^{*} (\boldsymbol x ) = {argmax}_{v} \; \sum_{k=1}^{R} \; \alpha_{k} \; I(C_{k} (\boldsymbol x) = v ) \) |
Classify the data in Table 7.6.1 of Example 7.6.1 below using the Adaboosting ensemble method. The classifier in each round uses a minimum entropy decision stump.
| Table 7.6.1 10 customer data with income \(x\) and purchase status \(y\) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \(x\) | 100 | 120 | 160 | 180 | 186 | 190 | 210 | 250 | 270 | 300 |
| \(y\) | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 |
Answer
Since the number of data is \(n\) = 10, at first, as in bagging, the probability of each data being selected is given equally as \(\frac{1}{10}\) = 0.1, and then 10 new bootstrap sampling data are extracted with replacement. Assume that the data extracted by this method are as follows, the minimum entropy classifier \(C_{1}\) is as shown in Table 7.6.4.
| Table 7.6.4 (Sample 1) 10 bootstrap samples for AdaBoosting and classifier \(C_{1}\) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| number | Bootstrap sample | Classifier \(C_{1}\) | ||||||||||
| Sample 1 | \(x\) | 100 | 180 | 186 | 190 | 190 | 210 | 216 | 210 | 250 | 300 | If \(x ≤ 230\), then \(y\) = -1, else \(y\) = 1 |
| \(y\) | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | ||
The classification results of the original data using the classifier \(C_{1}\) and the process of updating the new probability of selection are as in Table 7.6.5.
| Table 7.6.5 Process of updating the new probability of selection using \(C_{1}\) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Selction probability \(p_{i}^{(1)}\) | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| \(x_{i}\) | 100 | 120 | 160 | 180 | 186 | 190 | 210 | 250 | 270 | 300 |
| \(y_{i}\) | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 |
| Classification by \(C_{1} (x_{i})\) | -1 | -1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 |
| \(I(C_{1} (x_{i}) \ne y_{i} )\) | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(p_{i}^{(1)}\; I(C_{1} (x_{i}) \ne y_{i} )\) | 0.1 | 0.1 | 0.1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(\epsilon_{1} = 0.03\), \(\quad \alpha_{1} \;=\; \frac{1}{2} \; ln \; \frac{1- \epsilon_{1}}{\epsilon_{1}}\) = 1.738 | ||||||||||
| \( \begin{align} e^{-\alpha_{1}} \quad if \; C_{1} (\boldsymbol x_{i}) \;=\; y_{i} \\ e^{\alpha_{1}} \; \quad if \; C_{1} (\boldsymbol x_{i}) \;\ne\; y_{i} \\ \end{align} \) | 5.686 | 5.686 | 5.686 | 0.176 | 0.176 | 0.176 | 0.176 | 0.176 | 0.176 | 0.176 |
| \(p_{i}^{(1)} \; \times \) above row | 0.569 | 0.569 | 0.569 | 0.018 | 0.018 | 0.018 | 0.018 | 0.018 | 0.018 | 0.018 |
| \(Z_{1} = 1.829\) | ||||||||||
| New selction probability \(p_{i}^{(2)}\) | 0.311 | 0.311 | 0.311 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 |
The 10 new bootstrap sampling data extracted with replacement using the new selection probability and the classifier \(C_{2}\) at this time are as shown in Table 7.6.5.
| Table 7.6.5 (Sample 2) 10 bootstrap samples for AdaBoosting and classifier \(C_{2}\) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| number | Bootstrap sample | Classifier \(C_{2}\) | ||||||||||
| Sample 2 | \(x\) | 100 | 120 | 120 | 120 | 120 | 120 | 160 | 160 | 160 | 160 | If \(x ≤ 50\), then \(y\) = -1, else \(y\) = 1 |
| \(y\) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
The classification results of the original data using the classifier \(C_{2}\) and the process of updating the new probability of selection are as in Table 7.6.6.
| Table 7.6.6 Process of updating the new probability of selection using \(C_{2}\) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Selction probability \(p_{i}^{(2)}\) | 0.311 | 0.311 | 0.311 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 |
| \(x_{i}\) | 100 | 120 | 160 | 180 | 186 | 190 | 210 | 250 | 270 | 300 |
| \(y_{i}\) | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 |
| Classification by \(C_{2} (x_{i})\) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| \(I(C_{2} (x_{i}) \ne y_{i} )\) | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| \(p_{i}^{(2)}\; I(C_{2} (x_{i}) \ne y_{i} )\) | 0 | 0 | 0 | 0.010 | 0.010 | 0.010 | 0.010 | 0 | 0 | 0 |
| \(\epsilon_{2} = 0.004\), \(\quad \alpha_{2} \;=\; \frac{1}{2} \; ln \; \frac{1- \epsilon_{2}}{\epsilon_{2}}\) = 2.758 | ||||||||||
| \( \begin{align} e^{-\alpha_{2}} \quad if \; C_{2} (\boldsymbol x_{i}) \;=\; y_{i} \\ e^{\alpha_{2}} \; \quad if \; C_{2} (\boldsymbol x_{i}) \;\ne\; y_{i} \\ \end{align} \) | 0.063 | 0.063 | 0.063 | 15.78 | 15.78 | 15.78 | 15.78 | 0.063 | 0.063 | 0.063 |
| \(p_{i}^{(2)} \; \times \) above row | 0.02 | 0.02 | 0.02 | 0.158 | 0.158 | 0.158 | 0.158 | 0.006 | 0.006 | 0.006 |
| \(Z_{2} = 0.6922\) | ||||||||||
| New selction probability \(p_{i}^{(3)}\) | 0.028 | 0.028 | 0.028 | 0.228 | 0.228 | 0.228 | 0.228 | 0.001 | 0.001 | 0.001 |
The 10 new bootstrap sampling data extracted with replacement using the new selection probability and the classifier \(C_{3}\) at this time are as shown in Table 7.6.7.
| Table 7.6.7 (Sample 3) 10 bootstrap samples for AdaBoosting and classifier \(C_{3}\) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| number | Bootstrap sample | Classifier \(C_{3}\) | ||||||||||
| Sample 3 | \(x\) | 120 | 120 | 180 | 180 | 180 | 180 | 186 | 190 | 190 | 210 | If \(x ≤ 150\), then \(y\) = 1, else \(y\) = -1 |
| \(y\) | 1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | ||
The classification results of the original data using the classifier \(C_{3}\) and the process of updating the new probability of selection are as in Table 7.6.8.
| Table 7.6.8 Process of updating the new probability of selection using \(C_{3}\) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Selction probability \(p_{i}^{(3)}\) | 0.028 | 0.028 | 0.028 | 0.228 | 0.228 | 0.228 | 0.228 | 0.001 | 0.001 | 0.001 |
| \(x_{i}\) | 100 | 120 | 160 | 180 | 186 | 190 | 210 | 250 | 270 | 300 |
| \(y_{i}\) | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 |
| Classification by \(C_{3} (x_{i})\) | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
| \(I(C_{3} (x_{i}) \ne y_{i} )\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| \(p_{i}^{(3)}\; I(C_{3} (x_{i}) \ne y_{i} )\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.001 | 0.001 |
| \(\epsilon_{3} = 0.0003\), \(\quad \alpha_{3} \;=\; \frac{1}{2} \; ln \; \frac{1- \epsilon_{3}}{\epsilon_{3}}\) = 4.0557 | ||||||||||
| \( \begin{align} e^{-\alpha_{3}} \quad if \; C_{3} (\boldsymbol x_{i}) \;=\; y_{i} \\ e^{\alpha_{3}} \; \quad if \; C_{3} (\boldsymbol x_{i}) \;\ne\; y_{i} \\ \end{align} \) | 0.017 | 0.017 | 0.017 | 0.017 | 0.017 | 0.017 | 0.017 | 57.73 | 57.73 | 57.73 |
| \(p_{i}^{(3)} \; \times \) above row | 0.0005 | 0.0005 | 0.0005 | 0.004 | 0.004 | 0.004 | 0.004 | 0.058 | 0.058 | 0.058 |
| \(Z_{3} = 0.1904\) | ||||||||||
| New selction probability \(p_{i}^{(4)}\) | 0.003 | 0.003 | 0.003 | 0.021 | 0.021 | 0.021 | 0.021 | 0.303 | 0.303 | 0.303 |
For classification results of each classifier, the weighted sum is calculated using the classifier importance \(\alpha_{k}\), and the sign is examined to perform the final classification as shown in Table 7.6.9. Each classifier has an accuracy of about 70% at best, but it can be seen that all data are classified accurately due to AdaBoosting method.
| Table 7.6.9 Final classification results using AdaBootstrap | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(x_{i}\) | 100 | 120 | 160 | 180 | 186 | 190 | 210 | 250 | 270 | 300 | Classifier importance | |
| \(C_{1} (x_{i})\) classification result | -1 | -1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | \(\alpha_{1} = 1.738\) | |
| \(C_{2} (x_{i})\) classification result | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | \(\alpha_{2} = 2.758\) | |
| \(C_{3} (x_{i})\) classification result | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | \(\alpha_{3} = 4.055\) | |
| Weighted sum of classification result | 5.08 | 5.08 | 5.08 | -3.04 | -3.04 | -3.04 | -3.04 | 0.44 | 0.44 | 0.44 | ||
| Final classification result (sign) | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | ||
7.6.4 R and Python practice - Adaboosting
R and Python practice
R practice
[Colab]
| boosting {adabag} | Applies the AdaBoost.M1 and SAMME algorithms to a data set Fits the AdaBoost.M1 (Freund and Schapire, 1996) and SAMME (Zhu et al., 2009) algorithms using classification trees as single classifiers. |
|---|---|
| boosting(formula, data, boos = TRUE, mfinal = 100, coeflearn = 'Breiman', control,...) | |
| formula | a formula, as in the lm function. |
| data | a data frame in which to interpret the variables named in the formula |
| boos | if TRUE (by default), a bootstrap sample of the training set is drawn using the weights for each observation on that iteration. If FALSE, every observation is used with its weights. |
| mfinal | an integer, the number of iterations for which boosting is run or the number of trees to use. Defaults to mfinal=100 iterations. |
| coeflearn | if 'Breiman'(by default), alpha=1/2ln((1-err)/err) is used. If 'Freund' alpha=ln((1-err)/err) is used. In both cases the AdaBoost.M1 algorithm is used and alpha is the weight updating coefficient. On the other hand, if coeflearn is 'Zhu' the SAMME algorithm is implemented with alpha=ln((1-err)/err)+ ln(nclasses-1). |
| control | options that control details of the rpart algorithm. See rpart.control for more details. |
| Details: AdaBoost.M1 and SAMME are simple generalizations of AdaBoost for more than two classes. In AdaBoost-SAMME the individual trees are required to have an error lower than 1-1/nclasses instead of 1/2 of the AdaBoost.M1 | |
| Value: An object of class boosting, which is a list with the following components: | |
| formula | the formula used. |
| trees | the trees grown along the iterations. |
| weights | a vector with the weighting of the trees of all iterations. |
| votes | a matrix describing, for each observation, the number of trees that assigned it to each class, weighting each tree by its alpha coefficient. |
| prob | a matrix describing, for each observation, the posterior probability or degree of support of each class. These probabilities are calculated using the proportion of votes in the final ensemble. |
| class | the class predicted by the ensemble classifier. |
| importance | returns the relative importance of each variable in the classification task. This measure takes into account the gain of the Gini index given by a variable in a tree and the weight of this tree. |
An example of R commands for the adaboosting ensemble model using the iris data stored in R is as follows.
| install.packages('adbag') |
| library(adabag) |
| data(iris) |
| # mfinal is an integer which is the number of iterations for which boosting is run iris.adaboost <- boosting(Species~., data = iris, boos = TRUE, mfinal = 10) |
| # list the importance of variable in the classification iris.adaboost$importance Petal.Length Petal.Width Sepal.Length Sepal.Width 61.558263 26.329296 5.586443 6.525997 |
| # list the trees grown along the iterations. iris.adaboost$trees
[[1]]
n= 150
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 150 94 virginica (0.32666667 0.30000000 0.37333333)
2) Petal.Length< 2.45 49 0 setosa (1.00000000 0.00000000 0.00000000) *
3) Petal.Length>=2.45 101 45 virginica (0.00000000 0.44554455 0.55445545)
6) Petal.Width< 1.75 49 4 versicolor (0.00000000 0.91836735 0.08163265)
12) Petal.Length< 4.95 42 0 versicolor (0.00000000 1.00000000 0.00000000) *
13) Petal.Length>=4.95 7 3 virginica (0.00000000 0.42857143 0.57142857) *
7) Petal.Width>=1.75 52 0 virginica (0.00000000 0.00000000 1.00000000) *
...
...
...
[[10]]
n= 150
node), split, n, loss, yval, (yprob)
* denotes terminal node
[[10]]
n= 150
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 150 77 virginica (0.1133333 0.4000000 0.4866667)
2) Petal.Length< 2.6 17 0 setosa (1.0000000 0.0000000 0.0000000) *
3) Petal.Length>=2.6 133 60 virginica (0.0000000 0.4511278 0.5488722)
6) Petal.Length< 5.15 96 36 versicolor (0.0000000 0.6250000 0.3750000)
12) Petal.Width< 1.75 65 13 versicolor (0.0000000 0.8000000 0.2000000)
24) Sepal.Length>=4.95 57 7 versicolor (0.0000000 0.8771930 0.1228070)
48) Petal.Length< 4.95 34 0 versicolor (0.0000000 1.0000000 0.0000000) *
49) Petal.Length>=4.95 23 7 versicolor (0.0000000 0.6956522 0.3043478)
98) Petal.Width>=1.55 16 0 versicolor (0.0000000 1.0000000 0.0000000) *
99) Petal.Width< 1.55 7 0 virginica (0.0000000 0.0000000 1.0000000) *
25) Sepal.Length< 4.95 8 2 virginica (0.0000000 0.2500000 0.7500000) *
13) Petal.Width>=1.75 31 8 virginica (0.0000000 0.2580645 0.7419355)
26) Sepal.Width>=3.15 8 0 versicolor (0.0000000 1.0000000 0.0000000) *
27) Sepal.Width< 3.15 23 0 virginica (0.0000000 0.0000000 1.0000000) *
7) Petal.Length>=5.15 37 0 virginica (0.0000000 0.0000000 1.0000000) *
|
| # plot the decision tree after iteration 10 data plot(iris.adaboost$trees[[10]]) |
text(iris.adaboost$trees[[10]]) 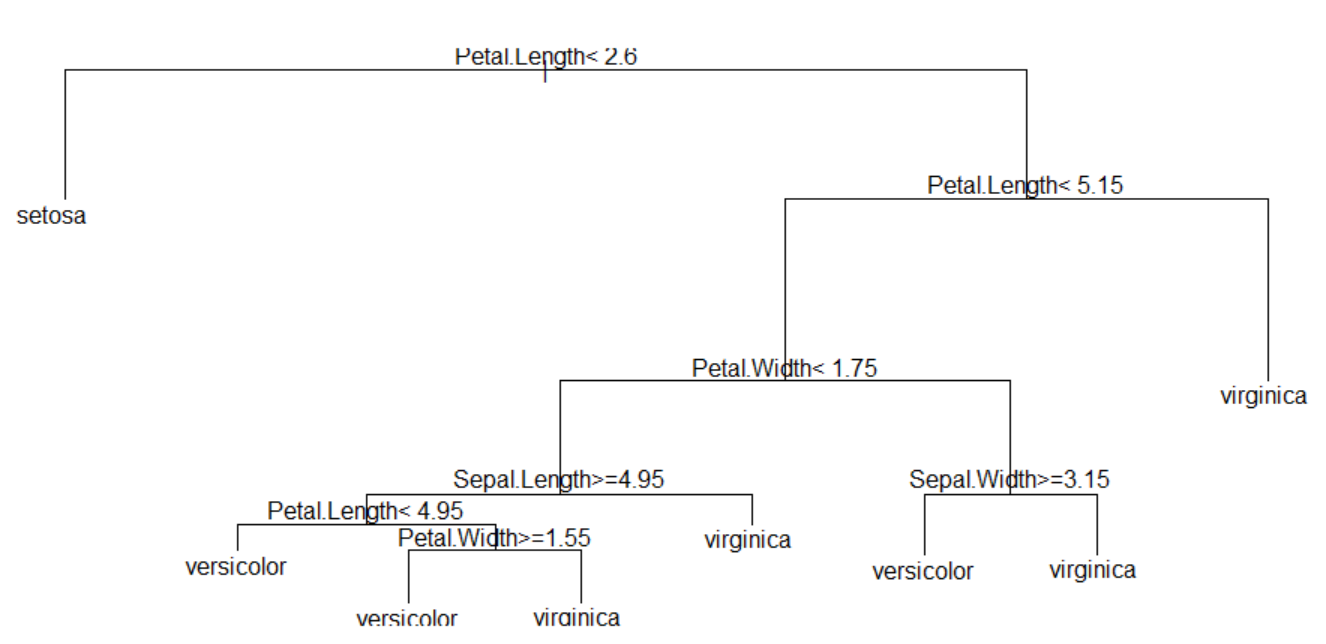
|
The R command to reclassify the entire iris data using the bagging model is as follows.
| # classify the iris data using the adaboosting model adaboostpred <- predict(iris.adaboost, newdata=iris) |
table(adaboostpred$class, iris[,5])
setosa versicolor virginica
setosa 50 0 0
versicolor 0 50 0
virginica 0 0 50
|
| # calculate the misclassification error adaboosttb <- table(adaboostpred$class, iris[,5]) |
| adaboosterror <- 1-(sum(diag(adaboosttb))/sum(adaboosttb)) |
| # misclassification error is 2.67% adaboosterror [1] 0 |
Python practice
[Colab]
|
# Import required libraries import pandas as pd import numpy as np from sklearn.ensemble import AdaBoostClassifier from sklearn.tree import DecisionTreeClassifier, plot_tree from sklearn.metrics import confusion_matrix import matplotlib.pyplot as plt from sklearn.datasets import load_iris # Load iris dataset iris = load_iris() iris_df = pd.DataFrame(data=iris.data, columns=iris.feature_names) iris_df['Species'] = iris.target species_map = {0: 'setosa', 1: 'versicolor', 2: 'virginica'} iris_df['Species'] = iris_df['Species'].map(species_map) # AdaBoost with decision trees (mfinal=10 iterations, boos=TRUE) adaboost_model = AdaBoostClassifier( n_estimators=10, random_state=0) X = iris_df.drop('Species', axis=1) y = iris_df['Species'] adaboost_model.fit(X, y) # Feature importance importance = adaboost_model.feature_importances_ feature_names = iris.feature_names importance_df = pd.Series(importance, index=feature_names) print("Feature Importance:\n", importance_df) # List of trees (equivalent to iris.adaboost$trees) trees = adaboost_model.estimators_ print("List of Trees (number of trees):", len(trees)) for i, tree in enumerate(trees, 1): print(f"Tree {i}:", tree) Feature Importance: sepal length (cm) 0.000000 sepal width (cm) 0.000000 petal length (cm) 0.599859 petal width (cm) 0.400141 dtype: float64 List of Trees (number of trees): 10 Tree 1: DecisionTreeClassifier(max_depth=1, random_state=209652396) Tree 2: DecisionTreeClassifier(max_depth=1, random_state=398764591) Tree 3: DecisionTreeClassifier(max_depth=1, random_state=924231285) Tree 4: DecisionTreeClassifier(max_depth=1, random_state=1478610112) Tree 5: DecisionTreeClassifier(max_depth=1, random_state=441365315) Tree 6: DecisionTreeClassifier(max_depth=1, random_state=1537364731) Tree 7: DecisionTreeClassifier(max_depth=1, random_state=192771779) Tree 8: DecisionTreeClassifier(max_depth=1, random_state=1491434855) Tree 9: DecisionTreeClassifier(max_depth=1, random_state=1819583497) Tree 10: DecisionTreeClassifier(max_depth=1, random_state=530702035) |
7.6.5 Random forest
| Step 1 | Let \( D = \{(\boldsymbol x_{1}, y_{1}), (\boldsymbol x_{2}, y_{2}), ... , (\boldsymbol x_{n}, y_{n}) \}\) be the set of training data,
and \(m\) be the number of variables. |
| Step 2 | Let \(R\) be the number of random forest samples. |
| Step 3 | for k = 1 to Rdo |
| Step 4 | \(\qquad\)Generate random forest samples \(D_{k}\) with the subset of all variables. |
| Step 5 | \(\qquad\)Create classifier \(C_{k}\) using random forest samples \(D_{k}\) |
| Step 6 | end for |
| Step 7 | Classify an unknown data \(\boldsymbol x\) by the majority vote of each classifier. |
There have been many comparative studies on various ensemble methods. It is known that the efficiency of the Adaboosting method and the random forest method is relatively good as a result of experiments using actual data.
7.6.6 R and Python practice - Random forest
R practice
[Colab]
To use the random forest ensemble model using R, we need to install a package called randomForest. From the main menu of R, select ‘Package’ => ‘Install package(s)’, and a window called ‘CRAN mirror’ will appear. Here, select ‘0-Cloud [https]’ and click ‘OK’. Then, when the window called ‘Packages’ appears, select ‘randomForest’ and click ‘OK’. 'randomForest' is a package for modeling of the random forest ensemble model. General usage and key arguments of the function are described in the following table.
| randomForest {randomForest} | Classification and Regression with Random Forest randomForest implements Breiman's random forest algorithm (based on Breiman and Cutler's original Fortran code) for classification and regression. It can also be used in unsupervised mode for assessing proximities among data points. |
|---|---|
|
## S3 method for class 'formula' randomForest(formula, data=NULL, ..., subset, na.action=na.fail) ## Default S3 method: randomForest(x, y=NULL, xtest=NULL, ytest=NULL, ntree=500, mtry=if (!is.null(y) && !is.factor(y)) max(floor(ncol(x)/3), 1) else floor(sqrt(ncol(x))), weights=NULL, replace=TRUE, classwt=NULL, cutoff, strata, sampsize = if (replace) nrow(x) else ceiling(.632*nrow(x)), nodesize = if (!is.null(y) && !is.factor(y)) 5 else 1, maxnodes = NULL, importance=FALSE, localImp=FALSE, nPerm=1, proximity, oob.prox=proximity, norm.votes=TRUE, do.trace=FALSE, keep.forest=!is.null(y) && is.null(xtest), corr.bias=FALSE, keep.inbag=FALSE, ...) |
|
| data | an optional data frame containing the variables in the model. By default the variables are taken from the environment which randomForest is called from. |
| subset | an index vector indicating which rows should be used. (NOTE: If given, this argument must be named.) |
| na.action | A function to specify the action to be taken if NAs are found. (NOTE: If given, this argument must be named.) |
| x, formula | a data frame or a matrix of predictors, or a formula describing the model to be fitted (for the print method, an randomForest object). |
| y | A response vector. If a factor, classification is assumed, otherwise regression is assumed. If omitted, randomForest will run in unsupervised mode. |
| xtest | a data frame or matrix (like x) containing predictors for the test set. |
| ytest | response for the test set. |
| ntree | Number of trees to grow. This should not be set to too small a number, to ensure that every input row gets predicted at least a few times. |
| mtry | Number of variables randomly sampled as candidates at each split. Note that the default values are different for classification (sqrt(p) where p is number of variables in x) and regression (p/3) |
| weights | A vector of length same as y that are positive weights used only in sampling data to grow each tree (not used in any other calculation) |
| replace | Should sampling of cases be done with or without replacement? |
| classwt | Priors of the classes. Need not add up to one. Ignored for regression. |
| cutoff | (Classification only) A vector of length equal to number of classes. The ‘winning’ class for an observation is the one with the maximum ratio of proportion of votes to cutoff. Default is 1/k where k is the number of classes (i.e., majority vote wins). |
| strata | A (factor) variable that is used for stratified sampling. |
| samplesize | Size(s) of sample to draw. For classification, if sampsize is a vector of the length the number of strata, then sampling is stratified by strata, and the elements of sampsize indicate the numbers to be drawn from the strata. |
| nodesize | Minimum size of terminal nodes. Setting this number larger causes smaller trees to be grown (and thus take less time). Note that the default values are different for classification (1) and regression (5). |
| maxnodes | Maximum number of terminal nodes trees in the forest can have. If not given, trees are grown to the maximum possible (subject to limits by nodesize). If set larger than maximum possible, a warning is issued. |
| importance | Should casewise importance measure be computed? (Setting this to TRUE will override importance.) |
| localImp | Should casewise importance measure be computed? (Setting this to TRUE will override importance.) |
| nPerm | Number of times the OOB data are permuted per tree for assessing variable importance. Number larger than 1 gives slightly more stable estimate, but not very effective. Currently only implemented for regression. |
| proximity | Should proximity measure among the rows be calculated? |
| oob.prox | Should proximity be calculated only on “out-of-bag” data? |
| norm.votes | If TRUE (default), the final result of votes are expressed as fractions. If FALSE, raw vote counts are returned (useful for combining results from different runs). Ignored for regression. |
| do.trace | If set to TRUE, give a more verbose output as randomForest is run. If set to some integer, then running output is printed for every do.trace trees. |
| keep.forest | If set to FALSE, the forest will not be retained in the output object. If xtest is given, defaults to FALSE. |
| corr.bias | perform bias correction for regression? Note: Experimental. Use at your own risk. |
| keep.inbag | Should an n by ntree matrix be returned that keeps track of which samples are “in-bag” in which trees (but not how many times, if sampling with replacement) |
| Value: An object of class randomForest, which is a list with the following components: | |
| call | the original call to randomForest |
| type | one of regression, classification, or unsupervised. |
| predicted | the predicted values of the input data based on out-of-bag samples. |
| importance | a matrix with nclass + 2 (for classification) or two (for regression) columns. For classification, the first nclass columns are the class-specific measures computed as mean descrease in accuracy. The nclass + 1st column is the mean descrease in accuracy over all classes. The last column is the mean decrease in Gini index. For Regression, the first column is the mean decrease in accuracy and the second the mean decrease in MSE. If importance=FALSE, the last measure is still returned as a vector. |
| importanceSD | The “standard errors” of the permutation-based importance measure. For classification, a p by nclass + 1 matrix corresponding to the first nclass + 1 columns of the importance matrix. For regression, a length p vector. |
| localImp | a p by n matrix containing the casewise importance measures, the [i,j] element of which is the importance of i-th variable on the j-th case. NULL if localImp=FALSE. |
| ntree | number of trees grown. |
| mtry | number of predictors sampled for spliting at each node. |
| forest | (a list that contains the entire forest; NULL if randomForest is run in unsupervised mode or if keep.forest=FALSE. |
| err.rate | (classification only) vector error rates of the prediction on the input data, the i-th element being the (OOB) error rate for all trees up to the i-th. |
| confusion | (classification only) the confusion matrix of the prediction (based on OOB data). |
| votes | (classification only) a matrix with one row for each input data point and one column for each class, giving the fraction or number of (OOB) ‘votes’ from the random forest. |
| oob.times | number of times cases are ‘out-of-bag’ (and thus used in computing OOB error estimate) |
| proximity | if proximity=TRUE when randomForest is called, a matrix of proximity measures among the input (based on the frequency that pairs of data points are in the same terminal nodes). |
| mse | (regression only) vector of mean square errors: sum of squared residuals divided by n. |
| rsq | (regression only) “pseudo R-squared”: 1 - mse / Var(y). |
| test | if test set is given (through the xtest or additionally ytest arguments), this component is a list which contains the corresponding predicted, err.rate, confusion, votes (for classification) or predicted, mse and rsq (for regression) for the test set. If proximity=TRUE, there is also a component, proximity, which contains the proximity among the test set as well as proximity between test and training data. |
An example of R commands for the random forest ensemble model using the iris data stored in R is as follows.
| install.packages('randomForest') |
| library(randomForest) |
| data(iris) |
| iris.forest <- randomForest(Species~., data=iris, ntree = 100, proximity=TRUE) |
The R command to reclassify the entire iris data using the random forest model is as follows.
| # classify the iris data using the bagging model table(predict(iris.forest), iris[,5])
setosa versicolor virginica
setosa 50 0 0
versicolor 0 47 6
virginica 0 3 44
|
| # calculate the misclassification error foresttb <- table(predict(iris.forest), iris[,5]) |
| foresterror <- 1-(sum(diag(foresttb))/sum(foresttb)) |
| # misclassification error is 2.67% foresterror [1] 0.06 |
Python practice
[Colab]
|
# Import required libraries import pandas as pd import numpy as np from sklearn.ensemble import RandomForestClassifier from sklearn.metrics import confusion_matrix from sklearn.datasets import load_iris # Load iris dataset iris = load_iris() iris_df = pd.DataFrame(data=iris.data, columns=iris.feature_names) iris_df['Species'] = iris.target species_map = {0: 'setosa', 1: 'versicolor', 2: 'virginica'} iris_df['Species'] = iris_df['Species'].map(species_map) # Random Forest with 100 trees and proximity rf_model = RandomForestClassifier(n_estimators=100, random_state=0, oob_score=True) # oob_score approximates proximity X = iris_df.drop('Species', axis=1) y = iris_df['Species'] rf_model.fit(X, y) # Predict on the iris dataset rf_pred = rf_model.predict(X) # Confusion matrix conf_matrix = confusion_matrix(y, rf_pred, labels=['setosa', 'versicolor', 'virginica']) conf_matrix_df = pd.DataFrame(conf_matrix, index=['setosa', 'versicolor', 'virginica'], columns=['setosa', 'versicolor', 'virginica']) print("Confusion Matrix:\n", conf_matrix_df) # Calculate misclassification error forest_error = 1 - (np.diag(conf_matrix).sum() / conf_matrix.sum()) print("Misclassification Error:", forest_error) print("Misclassification Error (%):", forest_error * 100, "%")
Confusion Matrix:
setosa versicolor virginica
setosa 50 0 0
versicolor 0 50 0
virginica 0 0 50
Misclassification Error: 0.0
Misclassification Error (%): 0.0 %
|
7.7 Classification of multiple groups
When there are \(K\) classification groups, Let us denote them as \(G_{1},G_{2}, ... , G_{K}\). One way to apply a two-group classification method to the classification of multiple groups is to view the remaining groups as one group for each group \(G_{i}\), and view it as a two-group problem of {\(G_{i}\), other groups}. This is called the (1 : \(K-1\)) method. The second method is to classify the \(K\) groups into two pairwise groups {\(G_{i}, G_{j}\)}, which requires the creation of \({}_{K} C_{2} = \frac{K(K-1)}{2}\) classifiers, and it is called the (1:1) method. When creating a classifier, data that do not belong to two groups {\(G_{i}, G_{j}\)} are ignored. When classifying data whose group membership is unknown, a method of applying multiple classifiers and classifying them into one group by majority vote is often used. There is a possibility of obtaining equal votes when using a majority vote. To prevent this, if the results of the two-group classification are expressed as the probability of belonging to each group, then these are combined to classify them into the group with the higher probability.
Suppose there are 4 classification groups {\(G_{1}, G_{2}, G_{3}, G_{4}\)} and Let us apply the (1:3) method. For example, if (\(G_{1} : \{G_{2}, G_{3}, G_{4}\}\)), was applied to one data whose group affiliation was unknown, it was classified into \(G_{1}\) group, Let us denote it as + group. if (\(G_{2} : \{G_{1}, G_{3}, G_{4}\}\)) was applied to the data, it was classified into \(\{G_{1}, G_{3}, G_{4}\}\) group, Let us denote it as - group. Similarly, if (\(G_{3} : \{G_{1}, G_{2}, G_{4}\}\)) was applied to the data, it was classified into \(\{G_{1}, G_{2}, G_{4}\}\) group, which is - group, if (\(G_{4} : \{G_{1}, G_{2}, G_{3}\}\)) was applied to the data, it was classified into \(\{G_{1}, G_{2}, G_{3}\}\) group, which is - group. The classification results are summarized as in Table 7.7.1. What is the final classification result of the data using (1:3) method?
| Table 7.7.1 Classification results of (1:3) method | ||||
|---|---|---|---|---|
| Method (1:3) groups | + : \(G_{1}\) - : \(\{G_{2}, G_{3}, G_{4}\}\) |
+ : \(G_{2}\) - : \(\{G_{1}, G_{3}, G_{4}\}\) |
+ : \(G_{3}\) - : \(\{G_{1}, G_{2}, G_{4}\}\) |
+ : \(G_{4}\) - : \(\{G_{1}, G_{2}, G_{3}\}\) |
| Classification result | + | - | - | - |
When we applied the (1:1) method to the same data, there are 6 classification and their classification results are summarized as in Table 7.7.2. What is the final classification result of the data using (1:1) method?
| Table 7.7.2 Classification results of (1:3) method | |||||||
|---|---|---|---|---|---|---|---|
| Method (1:1) groups | + : \(G_{1}\) - : \(G_{2}\) |
+ : \(G_{1}\) - : \(G_{3}\) |
+ : \(G_{1}\) - : \(G_{4}\) |
+ : \(G_{2}\) - : \(G_{3}\) |
+ : \(G_{2}\) - : \(G_{4}\) |
+ : \(G_{3}\) - : \(G_{4}\) |
|
| Classification result | + | + | - | + | - | + | |
Answer
The classification results of (1:3) method ,as shown in Table 7.7.1 means that \(G_{1}\) group receives 4 votes and the other groups receive 2 votes. Therefore, the data is classified into the \(G_{1}\) group by the majority vote.
When applying the (1:1) method, the \(G_{1}\) and \(G_{4}\) groups receive 2 votes, and the \(G_{2}\) and \(G_{3}\) groups receive 1 vote, and are classified into the \(G_{1}\) or \(G_{4}\) group.
7.8 Exercise
7.1 The SAT scores (out of 100) and essay scores of 10 accepted applicants, denoted P, for a college, 10 failed applicants, denoted N, are as follows.
| Group | SAT | Essay |
|---|---|---|
| P | 96 | 95 |
| P | 86 | 83 |
| P | 76 | 88 |
| P | 73 | 89 |
| P | 85 | 80 |
| P | 83 | 81 |
| P | 92 | 80 |
| P | 93 | 95 |
| P | 87 | 90 |
| P | 92 | 90 |
| N | 76 | 70 |
| N | 82 | 70 |
| N | 80 | 80 |
| N | 70 | 85 |
| N | 65 | 75 |
| N | 71 | 72 |
| N | 72 | 80 |
| N | 70 | 65 |
| N | 64 | 70 |
| N | 73 | 80 |
7.2 The following is a survey of 10 people visiting a department store to determine whether they purchased a product and their age. Those who purchased were denoted as Y, those who did not purchase were denoted as N. The data were sorted in ascending order of age. We want to divide age into two groups to apply a decision tree model. What is the best boundary value for the division?
| Group | Age |
|---|---|
| N | 25 |
| N | 27 |
| N | 31 |
| Y | 33 |
| N | 35 |
| Y | 41 |
| N | 43 |
| Y | 49 |
| Y | 51 |
| Y | 55 |