Chapter 4. Probability and distribution
[presentation] [book]
- 4.1 Probability
- 4.1.1 Calculation rules of probability and conditional probability
- 4.1.2 Bayes theorem
- 4.2 Random variable and distribution
- 4.2.1 Binomial distribution
- 4.2.2 Normal distribution
- 4.3 Multivariate distribution
- 4.4 Estimation of a distribution
- 4.5 Exercise
CHAPTER OBJECTIVES
4.1 Probability
[presentation] [video]
These examples have common characteristics as follows.
Events with these three characteristics are subject to study and to apply statistics. An experiment in which a particular outcome occurs among known possible outcomes is called a statistical experiment. In a statistical experiment, the resulting outcome is uncertain and is determined by chance. For example, if you throw a coin, the possible outcomes are either the head or tail, but the resulting outcome will come out by chance, so tossing a coin is a statistical experiment. If a production plant produces products at one machine and their possible outcomes are either defective or normal, then producing a product is a statistical experiment. Also, a pizza delivery time to your home, which takes between 20 and 60 minutes, is a statistical experiment.
In a statistical experiment, the set of all possible outcomes is referred to as a sample space, and a subset of this sample space is referred to as an event. The sample space is usually denoted by S, and events of the sample space are denoted by English capital letters as A, B, and C ... In the example above, a machine produces a product, the sample space is S = {normal, defective} and a subset of the sample space such as A = {defective} is an event. As such, when the number of elements in a sample space is either finite or countably infinite, it is called a discrete sample space. In a statistical experiment of the pizza delivery time to home, the sample space is all possible time between 20 minutes and 60 minutes, i.e. S = { (20,60) }. Delivery time between 20 and 30 minutes ({20,30}) is an event. As such, when the number of elements in a sample space is uncountably infinite, it is called a continuous sample space.
A concept of probability is used to indicate the possibility of an event occurring in a statistical experiment. The probability represents the likelihood of an event occurring using a number between 0 and 1. If an event is likely to occur, the probability is expressed as a number close to 1. The probability is expressed as a number close to zero if it is unlikely. Specifically, there are several ways to define the probability of an event using a number between zero and one. We introduce two definitions of the probability, one is a classical definition and the other is a relative definition of the probability. Assuming all elements in the sample space are likely to occur equally. The classical definition of probability that an event A will occur, denoted as P(A), in case of the discrete sample space is defined as follows: $$ \small P(A) = \frac {\text {Number of elements belonging to an event A}} {\text {Total number of elements in sample space}} $$ The probability that an event A will occur in case of the continuous sample space is defined as follows. $$ \small P(A) = \frac {\text {Measurement of elements belonging to an event A}} {\text {Measurement of the total elements of a sample space} } $$ The measurement can be the length, area, and volume, etc.
Answer
The sample space in this statistical experiment, which counts the number of points on the top by throwing a dice, is {1, 2, 3, 4, 5, 6}, and the number of odd events is {1, 3, 5}, so there are three elements. Therefore, the probability that restaurant A will be selected is 3/6 = 1/2.
Answer
The sample space in this example is all values from 10 to 30 minutes collectively { (10,30) }, and where a pizza is delivered between 20 and 25 minutes is the event { (20,25) }. Therefore, the probability of this event is \( \small \frac {(25-20)} { (30-10)} = 0.25 \) by measuring the distance of the interval.
A simulation of a coin toss experiment using 『eStatU』 shows that the relative frequency of ‘Head’ occurrence converges to the probability of one-half. This convergence of the probability is called the law of large numbers.
4.1.1 Calculation rules of probability and conditional probability
Answer
Since 25 students took Economics and 20 students are taking both courses, 25 - 20 = 5 students take only Economics. Also, since 30 students are taking Political Science, 30 - 20 = 10 students take only Political Science. Thus, as shown in <Figure 4.1.1>, the number of students taking either Economics or Political Science is 5 + 10 + 20 = 35. Therefore, the probability of students taking either Economics or Political Science is 35 / 40.
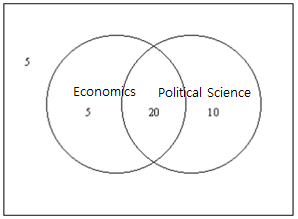
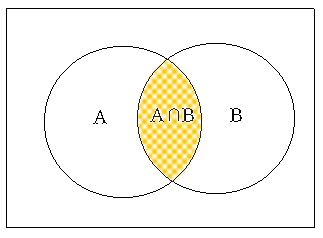
Consider students taking both Economics (A) and Political Science (B). The event that a student took both courses, denoted as A ∩ B, is called an intersection event of A and B (<Figure 4.1.2>).
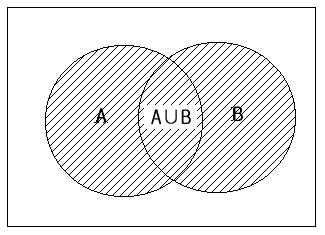
The event that a student takes either Economics or Political Science (one or both), denoted as A ∪ B, is called an union event of A and B (<Figure 4.1.3>).
Probabilities of these events on this example are as follows:
P(B) = 30 / 40 = 0.750
P(A ∩ B) = 20 / 40 = 0.500
P(A ∪ B) = 35 / 40 = 0.875
The probability of P(A ∪ B) can also be calculated as follows if you look at the <Figure 4.1.1>.
That is, the probability of taking either Economics or Political Science, P(A ∪ B), can be calculated by adding the probability of taking each course and subtracting the probability of taking both courses.
[Addition Rule of Probability]
Answer
In this case, because no student takes both courses, the events in which they take Economics (A) and Political Science (B) are mutually exclusive. Thus, the probability taking either Economics or Political Science, P(A U B), is as follows:
Answer
To solve this problem, it is convenient to organize the information given into a cross table as shown below.
| Baku | Province | Total | |
|---|---|---|---|
| Male | 1 | 10 | |
| Female | 5 | 20 | |
| Total | 24 | 6 | 30 |
If we calculate and insert the blanks in the above table, it is as follows. Let us call the event of the male as M, the female as F, from Baku as B, from the province as C.
| Baku(B) | Province(C) | Total | |
|---|---|---|---|
| Male(M) | 9 | 1 | 10 |
| Female(F) | 15 | 5 | 20 |
| Total | 24 | 6 | 30 |
1) \(\small P(C) = \) 6/30.
2) The probability that this student is from the province among females is 5/20. This probability is denoted as \(\small P(C∣F) \) and is called a conditional probability.
3) The probability of a male from the province is \(\small P(M∣C) = \) 1/6.
4) The probability is \(\small P(M ∩ B) \) and the cross table shows that the answer is 9/30. Alternatively, the probability of the male among all students can be obtained as \(\small P(M) = \) (10/30) and then multiplied by the conditional probability of being from Baku among the males, \(\small P(B∣M) \) = 9/10. Namely
\( \qquad \small P(M ∩ B) = P(M) P(B∣M) = (10/30) \times (9/10) = 9/30 \)
This expression shows that the conditional probability \(\small P(B∣M) \) can be calculated by dividing \(\small P(M ∩ B) \) by \(\small P(M) \).
\( \qquad \small P(B ∣ M) = \frac {P(M ∩ B)} {P(M)} = \frac { 9/30} {10/30} = \frac {9} {10} \)
In addition, the probability \( \small P(M ∩ B) \) can be obtained first by the probability of being a student from Baku, \(\small P(B) = \) 24/30, and then multiplied by the probability of being a male from Baku (\(\small P(M∣B) = \) 9/24).
\( \qquad \small P(M ∩ B) = P(B) P(M∣B) = (24/30) × (9/24) \)
[Multiplication Rule of Probability]
You can calculate the conditional probabilities and their graphs using 『eStatU』 as follows:
$$ \small P(A ∩ B) = P(A) P(B∣A) $$ If \(\small P(B∣A) = P(B) \), then the rule becomes as follows: $$ \small P(A ∩ B) = P(A) P(B) $$ In this case, the events \(\small A\) and \(\small B\) are called independent events.
Answer
Let us call the event that the Tiger wins the first game is \(\small A\), and the event that the Tiger wins the second game is \(\small B\). Since A and B are independent of each other, the probability that the Tiger will win both games is as follows.
\( \qquad \small P(A ∩ B) = P(A) P(B) = 0.7 × 0.7 = 0.49 \)
| Baku(B) | Province(C) | Total | |
|---|---|---|---|
| Male(M) | 5 | 5 | 10 |
| Female(F) | 10 | 10 | 20 |
| Total | 15 | 15 | 30 |
Answer
Let us call the event of male as \(\small M \), female as \(\small F\), from Baku as \(\small B\), and from the province as \(\small C \). From the table, probabilities of \(\small P(M ∩ B) \), \(\small P(M) \) and \(\small P(B) \) are as follows:
\( \qquad \small P(M ∩ B) = 5/30 \qquad P(M) = 10/30 \qquad P(B) = 15/30 \)
Therefore, the following relationship is satisfied:
\( \qquad \small P(M ∩ B) = P(M) P(B) \)
The events of male and Baku origin are independent of each other. Note that
\( \qquad \small P(M∣B) = 5/15 = 1/3 \qquad P(M)=10/30 \qquad \text{so, } \;\; P(M∣B) = P(M). \)
In this case, all events of both \(\small M \) and \(\small C \) , \(\small F \) and \(\small B \) , \(\small F \) and \(\small C \) are independent of each other. We call the two attributes, gender and region, independent of each other. In [Example 4.1.5], gender and region are not independent.
Answer
The probability of finding one defective in the three product tests is as follows.
\( \qquad \small \frac { _4 C_2 \times _2 C_1 } {_6 C_3 } = \frac {3}{5}. \)
The probability of finding two defective products is as follows.
\( \qquad \small \frac { _4 C_1 \times _2 C_2 } {_6 C_3 } = \frac {1}{5}. \)
Thus, the probability that at least one defect will be found is 3/5 + 1/5 = 4/5. Another way to calculate this probability is to obtain the probability of an event with no defect (a complementary event) and then subtract it from 1. In other words, the probability that at least one defective product can be calculated as follows.
\( \qquad \small 1 - \frac { _4 C_3 } {_6 C_3 } = 1 - \frac {4}{20} = \frac {4}{5}. \)
4.1.2 Bayes theorem
Suppose past surveys showed more information that if a person was tested for an immune response, a positive or negative response was shown. The probability that a hepatitis B carrier person showed a positive response to this test (called the sensitivity of the test) is 95%, and the probability that a non-hepatitis B carrier person showed a negative response (the specificity of the test) is 97%. This additional information about the probabilities of the immune response is called as likelihood probabilities. Using these probabilities, we are curious to find the following probabilities.
Answer
Let \(\small B\) be the event of being a hepatitis \(\small B\) carrier, \(\small G\) be the event of being a non-carrier, \(\small Y\) be the event of showing a positive response, and \(\small B\) be the event of showing a negative response. The information given in the problem is the probability of a hepatitis B carrier \(\small P(B)\) = 0.10, the conditional probability that a hepatitis B carrier will test positive \(\small P(Y∣B)\) = 0.95, and the conditional probability that a non-hepatitis Bcarrier will test negative \(\small P(N∣G)\) = 0.97. Since events \(\small B\) and \(\small G\), and events \(\small Y\) and \(\small N\) are mutually exclusive events, it is easy to see that \(\small P(G)\) = 0.90, \(\small P(N∣B) \) = 0.05, \(\small P(Y∣G) \) = 0.03. It is convenient to find related probabilities if we summarize the above values with a two-dimensional table as shown below,
| Positive (\(\small Y\)) | Negative (\(\small N\)) | Total | Likelihood probability | |
|---|---|---|---|---|
| Carrier (\(\small B\)) | \(\small P(B \cap Y)\) | \(\small P(B)\) = 0.10 | \(\small P(Y|B)\) = 0.95 \(\small P(N|B)\) = 0.05 |
|
| Non-carrier (\(\small G\)) | \(\small P(G \cap Y)\) | \(\small P(G)\) = 0.90 | \(\small P(Y|G)\) = 0.03 \(\small P(N|G)\) = 0.97 |
|
| Total | \(\small P(Y)\) | \(\small P(N)\) | 1.00 |
The probability that a person will show a positive response when he or she takes an immune response test in the question 1) is \(\small P(Y)\) and the probability of a hepatitis B carrier person showing a positive response, \(\small P(B \cap Y)\), and the probability of a non-hepatitis carrier person showing a positive response \(\small P(G \cap Y)\). In other words, $$ \small P(Y) = \small P(B \cap Y) + P(G \cap Y) $$ This is called a total probability that a person shows a positive response. The joint probabilities, \(\small P(B \cap Y)\) and \(\small P(G \cap Y)\), can be obtained as follows using the multiplication rule of probability. $$ \small \begin{align} P(B \cap Y) &= P(B) P(Y|B) = 0.1 \times 0.95 = 0.095 \\ P(G \cap Y) &= P(G) P(Y|B) = 0.9 \times 0.03 = 0.027 \end{align} $$ Therefore, $$ \small P(Y) = P(B \cap Y) + P(G \cap Y) = 0.095 + 0.027 = 0.122 $$ When a person shows a positive response in his immune test, the probability that this person is a hepatitis B carrier in question 2) is the proportion of a hepatitis B carrier and a positive response \(\small P(B \cap Y ) \) among all people who tested positive \(\small P(Y) \), which is the conditional probabiity \(\small P(B | Y ) \). From the definition of the conditional probability, it can be calculated as follows. $$ \small P(B | Y) = \frac {P(B \cap Y)} {P(Y)} = \frac {0.095}{0.122} = 0.779 $$ Since \( \small P(Y) = P(B \cap Y) + P(G \cap Y) \), the above formula can be written as follows. $$ \small P(B | Y) = \frac {P(B \cap Y)} {P(B \cap Y) + P(G \cap Y)} $$ When a person shows a positive response in his immune test, the probability that this person is a non-hepatitis B carrier can be calculated similarly as follows. $$ \small P(G | Y) = \frac {P(G \cap Y)} {P(Y)} = \frac {0.027}{0.122} = 0.221 $$ The probabilities \(\small P(B | Y) \) and \(\small P(G | Y) \) are called posterior probabilities to identify a person whether a hepatitis carrier or not using the likelihood probabilities.
Let the events \(\small A_1 , A_2 \;, ... ,\; A_n\) be mutually exclusive and \(\small S \;=\; A_1 ∪ A_2 \;∪ ... ∪ \;A_n\) is the sample space. If the event \(\small Y\) is \(\small P(Y) > 0 \), and the prior probabilities of \(\small P(A_1 ), P(A_2 ), ... , P(A_n) \) and the likelihood probabilities \(\small P(Y|A_1 ), P(Y|A_2 ), ..., P(Y|A_n ) \) are given, the posterior probability of \(\small P(A_k | Y) \) is as follows: $$ \small \begin{align} P(A_k | Y) &= \frac {P(A_k \cap Y)} {P(Y)} \\ &= \frac {P(A_k ) P(Y |A_k )} {P(A_1 ) P(Y |A_1 ) + P(A_2 ) P(Y |A_2 ) + \cdots + P(A_n ) P(Y |A_n ) } \end{align} $$
Answer
Let Y be the event that a product is defective. The information given in the problem can be summarized using a cross table as follows.
| Good (\(\small G\)) | Defective (\(\small Y\)) | Total | Defective rate Likelihood probability | |
|---|---|---|---|---|
| Machine \(\small A\) | \(\small P(A \cap Y)\) | \(\small P(A)\) = 0.40 | \(\small P(Y|A)\) = 0.05 which implies \(\small P(G|A)\) = 0.95 |
|
| Machine \(\small B\) | \(\small P(B \cap Y)\) | \(\small P(B)\) = 0.50 | \(\small P(Y|B)\) = 0.03 which implies \(\small P(G|B)\) = 0.97 |
|
| Machine \(\small C\) | \(\small P(C \cap Y)\) | \(\small P(C)\) = 0.10 | \(\small P(Y|C)\) = 0.01 which implies \(\small P(G|C)\) = 0.99 |
|
| Total | \(\small P(G)\) | \(\small P(Y)\) | 1.00 |
To find the probabilitiese of the above problem, we need to find the joint probabilities \(\small P(A \cap Y) ,\; P(B \cap Y),\; P(C \cap Y) \) in the cross table using the multiplication rule of probability as follows. $$ \small \begin{align} P(A \cap Y) &= P(A) P(Y|A) = 0.40 \times 0.05 = 0.020 \\ P(B \cap Y) &= P(B) P(Y|B) = 0.50 \times 0.03 = 0.015 \\ P(C \cap Y) &= P(C) P(Y|C) = 0.10 \times 0.01 = 0.001 \end{align} $$ Therefore, the total probability of the event that a product is defective, \(\small P(Y) \), is as follows. $$ \small \begin{align} P(Y) &= P(A \cap Y) + P(B \cap Y) + P(C \cap Y) \\ &= 0.020 + 0.015 + 0.001 = 0.036 \end{align} $$ We can summarize this calculation in the cross table as follows.
| Good (\(\small G\)) | Defective (\(\small Y\)) | Total | Defective rate Likelihood probability | |
|---|---|---|---|---|
| Machine \(\small A\) | 0.380 | 0.020 | \(\small P(A)\) = 0.400 | \(\small P(Y|A)\) = 0.050 which implies \(\small P(G|A)\) = 0.950 |
| Machine \(\small B\) | 0.485 | 0.015 | \(\small P(B)\) = 0.500 | \(\small P(Y|B)\) = 0.030 which implies \(\small P(G|B)\) = 0.970 |
| Machine \(\small C\) | 0.099 | 0.001 | \(\small P(C)\) = 0.100 | \(\small P(Y|C)\) = 0.010 which implies \(\small P(G|C)\) = 0.990 |
| Total | \(\small P(G)\) = 0.964 | \(\small P(Y)\) = 0.036 | 1.000 |
4.2 Random variable and probability distribution
Consider a statistical experiment in which a coin is thrown repeatedly two times. If the coin is ideal, the sample space for this experiment is {'Tail-Tail', 'Tail-Head', 'Head-Tail', 'Head-Head’}. The probability of an event in which each element of the sample space is produced is 1/4 by the classical definition. In most cases, the fact that we are interested in this example will be counting the number of heads or tails. If \(\small X\) is defined as 'the number of heads' in this experiment, the possible value of \(\small X\) can be 0, 1, or 2, and we are interested in calculating probabilities that \(\small X\)=0, \(\small X\)=1 or \(\small X\)=2. As such, a function that corresponds to one real number between [0,1] for each element of the sample space is called a random variable (see Table 4.2.1). When possible values of a random variable are finite or countably infinite, it is called a discrete random variable. If possible values of a random variable are uncountably infinite, it is called a continuous random variable.
| Table 4.2.1 Random variable \(\small X\) = 'Number of Heads’ when tossing a coin twice' | |
|---|---|
| Sample space | \(\small X\) = 'Number of Heads’ |
| Tail-Tail Tail-Head Head-Tail Head-Head |
0 1 1 2 |
| Table 4.2.2 Probability distribution function of \(\small X\) = 'Number of Heads’ when tossing a coin twice | |||||
|---|---|---|---|---|---|
| 1) Table style of the probability distribution function | 2) Function of the probability distribution function | ||||
|
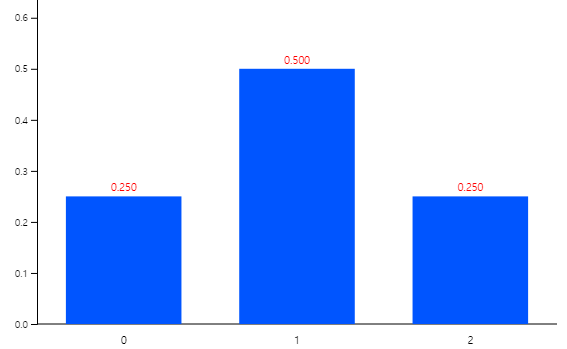
$$ \small \begin{align} f(x) &= 1/4, \qquad \text{if } x = 0 \\ &= 2/4, \qquad \text{if } x = 1 \\ &= 1/4, \qquad \text{if } x = 2 \\ \end{align} $$ | ||||
|
|||||
|
<Figure 4.2.1> Probability distribution function of the random variable \(\small X\) = 'Number of Heads’ when tossing a coin twice
|
|||||
Answer
Expectation and variance of \(\small X\) are as follows: $$ \small \begin{align} E(X) &= \mu = \sum_{i=1}^{n} x_{i} \text{P(X } = x_{i} ) = 0 \times \frac{1}{4} + 1 \times \frac{2}{4} + 2 \times \frac{1}{4} = 1 \\ V(X) &= \sigma^2 = \sum_{i=1}^{n} x_{i}^{2} \textrm{ P(X} = x_{i} )- \mu^{2} = 0^{2} \times \frac{1}{4} + 1^{2} \times \frac{2}{4} + 2^{2} \times \frac{1}{4} - 1^{2} = \frac{1}{2} \end{align} $$
Answer
The random variable \(\small X\) is the mid-term score and its mean and variance are \(\small E(X)\) = 60 and \(\small V(X)\) = 100.
1) The mean and variance of the new random variable \(\small X\) + 20 are as follows.
\(\qquad \small E(X + 20) = E(X) + 20 = 60 + 20 \)
\(\qquad \small V(X + 20) = V(X) = 100\)
2) The mean and variance of the new random variable \(\small 1.4 X\) are as follows.
\(\qquad \small E(1.4X) = 1.4 E(X) = 1.4 × 60 = 84\)
\(\qquad \small V(1.4X) = 1.4^2 V(X) = 1.96 × 100 = 196 \)
3) The mean and variance of the new random variable \(\small 1.2X + 10\) are as follows:
\(\qquad \small E(1.2X + 10) = 1.2 E(X) + 10 = 1.2 × 60 + 10 = 82 \)
\(\qquad \small V(1.2X + 10) = 1.2^2 V(X) = 1.44 × 100 = 144 \)
4.2.1 Binomial distribution
There are two possible outcomes {defective, normal} and {pro, con} in these examples, and the experiment is repeated, but we do not know the outcome of each experiment. Each experiment with two possible outcomes is specifically called a Bernoulli trial, and one outcome of interest in the two is often referred to as 'success' and the other outcome as 'failure'. This Bernoulli trial is usually repeated several times, and the number of successes is counted as follows:
The 'counting of successes' when performing the independently repeated Bernoulli trial with the same probability of success is called a binary random variable, and its distribution is called a binomial distribution. We will find the probability calculation of the binomial distribution in the example below.
Answer
This problem is the enforcement of the Bernoulli trial in each game of 'win' and 'fail'. This Bernoulli trial is repeated four times. The sample space is all about winning or losing a game, and their elements are shown below, marking the winning in O and the losing in X.
S = {‘XXXX’, ‘OXXX’, ‘XOXX’, ‘XXOX’, ‘XXXO’, ‘OOXX’, ‘OXOX’, ‘OXXO’, ‘XOOX’, ‘XOXO’, ‘XXOO’, ‘OOOX’, ‘OOXO’, ‘OXOO’, ‘XOOO’, ‘OOOO’}
1) The event that the Tiger loses all games is {'XXXX'}, and the probability of this event is (0.4)×(0.4)×(0.4)×(0.4) = \(\small (0.4)^4\).
2) There are four events that the Tiger wins once, and loses three times, such as {‘OXXX’, ‘XOXX’, ‘XXOX’, ‘XXXO’}. These four cases are equal to the number of O's in a single seat when there are four seats which is \(\small{}_4C_1\). Since the probability of each event is (0.6)×(0.4)×(0.4)×(0.4), the probability of the Tiger winning once is \(\small{}_4C_1 (0.6)(0.4)^3\).
3) There are six events that the Tiger wins two times and loses two times, such as {‘OOXX’, ‘OXOX’, ‘OXXO’, ‘XOOX’, ‘XOXO’, ‘XXOO’}. These six cases are equal to the number of O's in two seats when there are four seats which is \(\small{}_4C_2\). Since the probability of each event is (0.6)×(0.6)×(0.4)×(0.4), the probability of the Tiger winning twice is \(\small{}_4C_2 (0.6)^2(0.4)^2\).
4) There are four events that the Tiger wins three times and loses one time, such as {‘OOOX’, ‘OOXO’, ‘OXOO’, ‘XOOO’}. These four cases are equal to the number of O's in three seats when there are four seats which is \(\small{}_4C_3\). Since the probability of each event is (0.6)×(0.6)×(0.6)×(0.4), the probability of the Tiger winning three times is \(\small{}_4C_3 (0.6)^3(0.4)^1\).
5) There is one event that the Tiger wins four times such as {‘OOOO’}. This one case is equal to the number of O's in four seats when there are four seats which is \(\small{}_4C_4\). Since the probability of each event is (0.6)×(0.6)×(0.6)×(0.6), the probability of the Tiger winning all four times is \(\small{}_4C_4 (0.6)^4\).
6) The probability distribution function of the random variable X = ‘the number of games the Tiger wins’ is a summary of the above probabilities.
| \(\small X = x \) | \(\small P(X=x) \) |
|---|---|
| 0 | \(\small {}_{4}C_0 (0.4)^4 = 0.0256 \) |
| 1 | \(\small {}_{4}C_1 (0.6) (0.4)^3 = 0.1536 \) |
| 2 | \(\small {}_{4}C_2 (0.6)^2 (0.4)^2 = 0.3456 \) |
| 3 | \(\small {}_{4}C_3 (0.6)^3 (0.4) = 0.3456 \) |
| 4 | \(\small {}_{4}C_4 (0.6)^4 = 0.1296 \) |
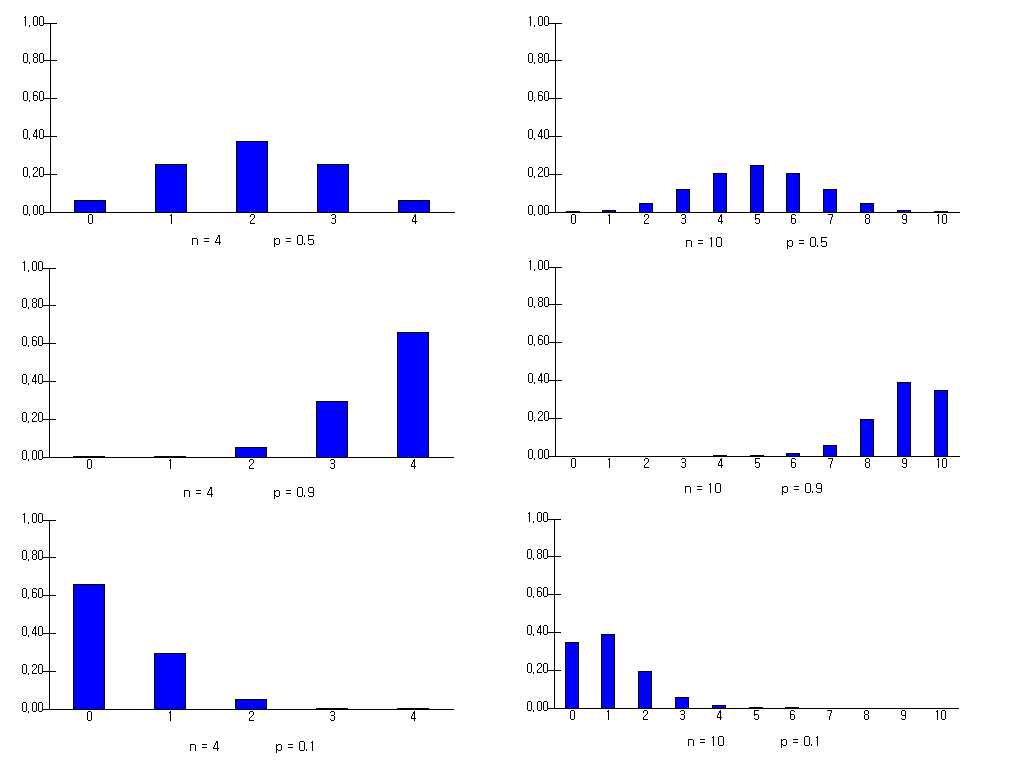
Using 『eStatU』, we can easily find this example's probability and probability distribution function. Select [Binomial Distribution] from the menu of 『eStatU』 and enter \(\small n = 4, p = 0.6\) and press the [Execute] button to display a binomial function graph. If you click the [Binomial Prob Table] button, a table of binomial probabilities appears.
[Binomial Distribution]
There are sliding bars of \(n\) and \(p\) and a probability calculation box under the graph, so put the desired value and press the [Enter] key to calculate the value.
A table of binomial distributions is shown to the right of the graph. In addition to \(\small P(X = x)\), this table shows the cumulative probabilities \(\small P(X \le x)\) and \(\small P(X \ge x)\) to facilitate various probability calculations. If you select a new \(n\) and \(p\) and click [Execute] button, a new binomial distribution table for this value is added below.
Answer
This example is a Binomial distribution with \(n = 10, p = 0.2\).
\( \qquad \quad \small P(X=3) = {}_{10} C_3 (0.2)^3 (1-0.2)^{10-3} = 0.2013 \)
$$ \small \begin{multline} \shoveleft \qquad \quad P(X \ge 2) = 1 - P(X=0) - P(X=1) = 1 - {}_{10} C_0 (0.2)^0 (1-0.2)^10 - {}_{10} C_1 (0.2)^1 (1-0.2)^{10-1} \\ \shoveleft \qquad \quad = 1 - 0.1074 - 0.2684 = 0.6242\\ \end{multline} $$
\( \qquad \quad \small E(X) = np = 10 × 0.2 = 2 \)
\( \qquad \quad \small V(X) = np(1-p) = 10 × 0.2 × 0.8 = 1.6 \)
\( \qquad \quad \small \sigma(X) = 1.265 \)
Select ‘Binomial Distribution’ from the menu of 『eStatU』, enter \(n=10, p=0.2\), and click on the [Execute] button to display a graph and Table 4.2.3. You can see the values in the above calculations, such as \(\small P(X \ge 2)\) = 0.6242
| Table 4.2.3 『eStatU』 Binomial Distribution Table when \(n = 10, p = 0.2\) | |||
|---|---|---|---|
| \(n = 10\) | \(p = 0.200\) | ||
| \(x\) | \(\small P(X = x)\) | \(\small P(X \le x)\) | \(\small P(X \ge x)\) |
| 0 | 0.1074 | 0.1074 | 1.0000 |
| 1 | 0.2684 | 0.3758 | 0.8926 |
| 2 | 0.3020 | 0.6778 | 0.6242 |
| 3 | 0.2013 | 0.8791 | 0.3222 |
| 4 | 0.0881 | 0.9672 | 0.1209 |
| 5 | 0.0264 | 0.9936 | 0.0328 |
| 6 | 0.0055 | 0.9991 | 0.0064 |
| 7 | 0.0008 | 0.9999 | 0.0009 |
| 8 | 0.0001 | 1.0000 | 0.0001 |
| 9 | 0.0000 | 1.0000 | 0.0000 |
| 10 | 0.0000 | 1.0000 | 0.0000 |
4.2.2 Normal distribution
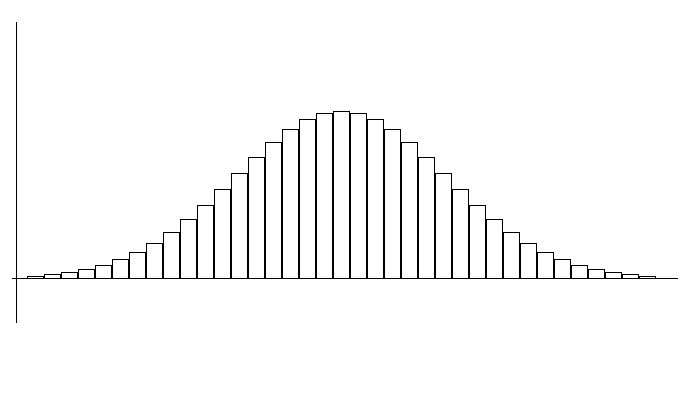
If you increase the number of data and close the interval's width to zero, this histogram can be approximated to a continuous function, as shown in <Figure 4.2.4>. This function is called a probability distribution function of the continuous random variable. In real life, many continuous data appear a bell-shaped function, as in <Figure 4.2.4>. The graph shows that large amounts of data are located around their mean, and fewer data are located as it moves away from the mean and is symmetrical about the mean. This type of probability distribution is called a normal distribution. Data obtained from measurements such as the height, weight, and bolt's length often follow the normal distribution.
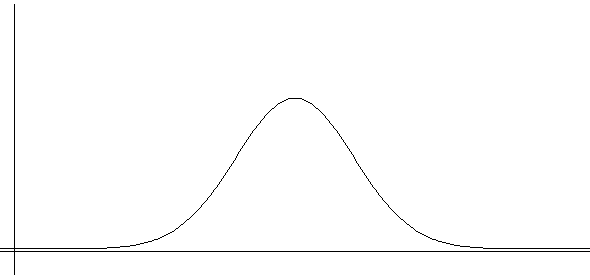
If the probability distribution function of a continuous random variable can be expressed as a mathematical function
\(f(x)\), we can approximate the desired probability easily without finding the frequency table and histogram.
The probability of the random variable \(\small X\) at interval (\(a,b) \), denoted as
\(\small {P( a \lt X \lt b) }\), can be obtained as the area between
(\(a,b) \) of \(f(x)\) as <Figure 4.2.5> which is the integral over (\(a,b) \) as follows:
$$
P(a \lt X \lt b)= \int_{a} ^{b} {} f(x)dx
$$
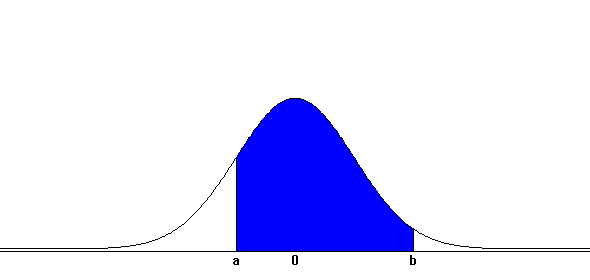
The total area under this function f(x) should be 1, because the addition of all probabilities is 1. $$ P(-∞ \lt X \lt ∞)= \int_{-∞} ^{∞} {} f(x)dx = 1 $$ The integral at an interval (\(a,b\)) of a function \(f(x)\) is generally difficult to obtain. For a normal distribution function, we use a table to calculate the probability or 『eStatU』 software, which will be discussed in this section.
Many mathematicians tried to find a mathematical function to describe this bell-shaped data type to make it easier to calculate probability. Abraham de Moivre (1667-1754) was the first to discover the function, and then Carl Friedrich Gauss (1777-1855) extensively applied to physics and astronomy. This function is called a normal distribution function or a Gaussian distribution function whose functional form is as follows. $$ f(x) = \frac{1}{\sqrt{2 π} \, \sigma } exp \{ - \frac {(x-\mu)^2 } {2 \sigma^2} \} $$ This distribution function has two parameters μ and σ, each representing the mean and standard deviation of the normal distribution. If \(X\) is a normal random variable with mean μ and variance \(\sigma^2\) , it is often denoted by a symbol \(X\) ~ \(N(\mu, \sigma^2)\). The following simulation of 『eStatU』, 'Normal Comparison', shows three normal distributions with different mean and variance such as \(N(0, 1)\), \(N(-2, 0.5^2 )\), and \(N(2, 3^2 )\). We can observe that all of them are symmetrical about the mean. If the variance increases, the normal distribution becomes flat, and if the variance decreases, the normal distribution becomes sharp. This is because the total area under the normal distribution function must be 1.
Probability Calculation of the Normal Distribution
In 『eStatU』, the calculation of probability \( P( a \lt X \lt b ) \) for the interval \((a , b)\) of any normal distribution \( N(\mu,\sigma^2) \) can be calculated. Any interval in the range of [ μ - 4σ, μ + 4σ ] can be calculated. Also, a percentile value \(x\) for a given probability \(p\), which is \(P( X \lt x) = p\), can be easily calculated using the following 'Normal Distribution' module.
The probability of \(\small P(Z \lt z)\) is near 0 if z is less than μ - 4σ and is 1 if z is greater than μ + 4σ.
Table 4.2.5 shows the percentiles of the standard normal distribution using 『eStatU』.
1) \(\small P(Z \lt 1.96)\)
2) \(\small P(-1.96 \lt Z \lt 1.96)\)
3) \(\small P(Z \gt 1.96)\)
Answer
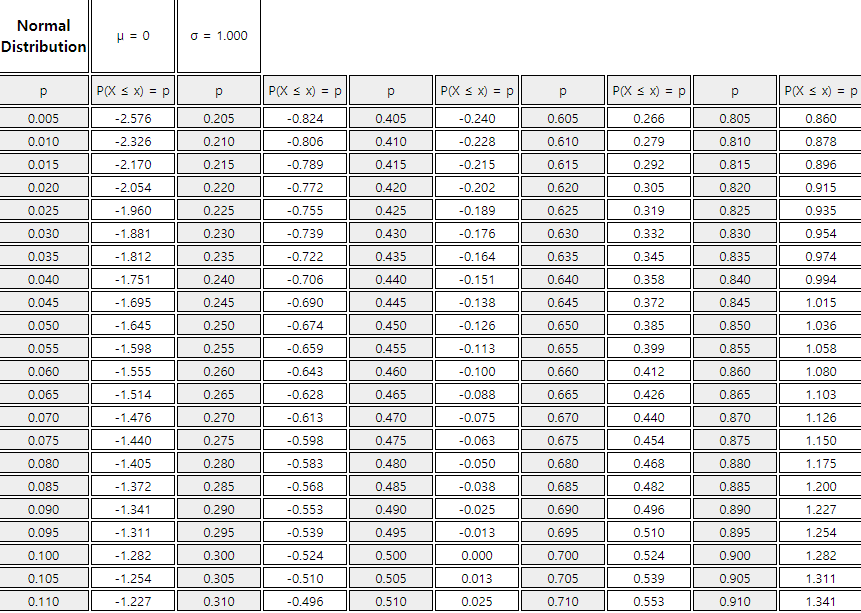
Using the standard normal distribution table,
1) \(\small P(Z \lt 1.96)\) = 0.975.
2) \(\small P(-1.96 \lt Z \lt 1.96) = P(Z \lt 1.96) - P(Z \lt -1.96)\) = 0.975 - 0.025 = 0.95
3) \(\small P(Z \gt 1.96) = 1 - P(Z \lt 1.96)\) = 1 - 0.975 = 0.025
Using the normal distribution module of 『eStatU』,
Answer
Using the percentile table of the standard normal distribution,
Using the normal distribution module of 『eStatU』,
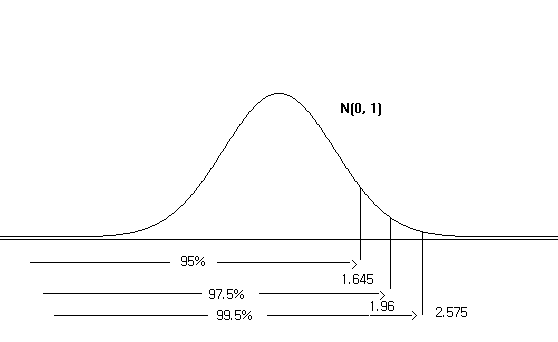
<Figure 4.2.7> shows 95% and 99% values when two ends are excluded equally.
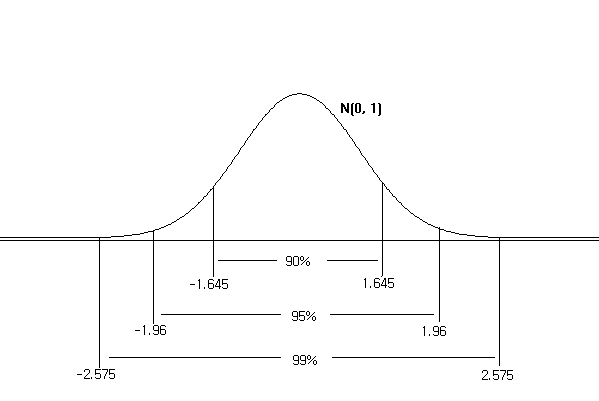
i.e., \(\small {P(-1.96 \lt Z \lt 1.96) }\) = 0.95, \(\small {P(-2.575 \lt Z \lt 2.575)}\) = 0.99
The probability of a general normal distribution can be obtained using the standard normal distribution table. As we studied, if \(X\) is a normal random variable with the mean μ and variance \(\sigma^2\), \(Z = \frac{X-\mu}{\sigma}\) follows the standard normal distribution. Therefore, the probability \( P( a \lt X \lt b ) \) of the interval \(( a, b )\) of \(\small X\) can be obtained from the standard normal distribution as follows. $$ P( a \lt X \lt b ) = P( \frac {a - \mu}{\sigma} \lt Z \lt \frac {b - \mu}{\sigma} ) $$
1) \(\small P(X \lt 94.3) \)
2) \(\small P(X \gt 57.7) \)
3) \(\small P(57.7 \lt X \lt 94.3) \)
Answer
Using the transformation to the standardized normal random variable, probability calculations are as follows:
1) \(\small P (X \lt 94.3) = P( \frac {X - 70}{10} \lt \frac {94.3 - 70}{10} ) = P( Z \lt 2.43) = 0.9925 \)
2) \(\small P (X \gt 57.7) = P( \frac {X - 70}{10} \gt \frac {57.7 - 70}{10} ) = P( Z \gt -1.23 = 0.8907\)
3) \(\small P (57.7 \lt X \lt 94.3) = P( \frac {57.7 - 70}{10} \lt \frac {X - 70}{10} \lt \frac {94.3 - 70}{10} ) = P(-1.23 \lt Z \lt 2.43 ) = 0.8832 \)
Using 『eStatU』, to obtain a probability of the normal distribution, enter the mean as 70 and the standard deviation as 10 at the top of the screen as <Figure 4.2.8>. For 1), enter 94.3 at the second option below the graph and then click the [Execute] button.
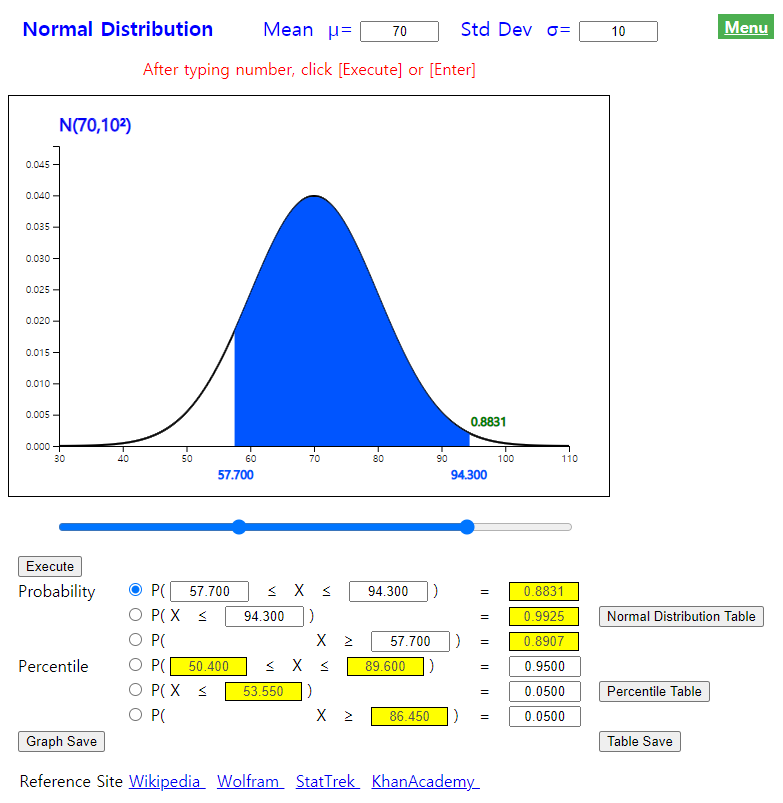
For 2), enter 57.7 at the third option below the graph and then click the [Execute] button.
For 3), enter the interval as (57.7, 94.3) at the first option below the graph and then click the [Execute] button.
1) What is the 95% percentile of the mid-term test scores?
2) What is the 95% percentile of two-sided type of the mid-term scores?
Answer
Using the normal probability table, percentile calculations are as follows:
Using 『eStatU』, to obtain the probability of normal distribution , enter the mean as 70 and the standard deviation as 10 at the top of the screen as <Figure 4.2.9>.
For 1), enter 0.95 at the box of the fifth option below the graph and click the [Execute] button to display the 95 percentile as 86.449.
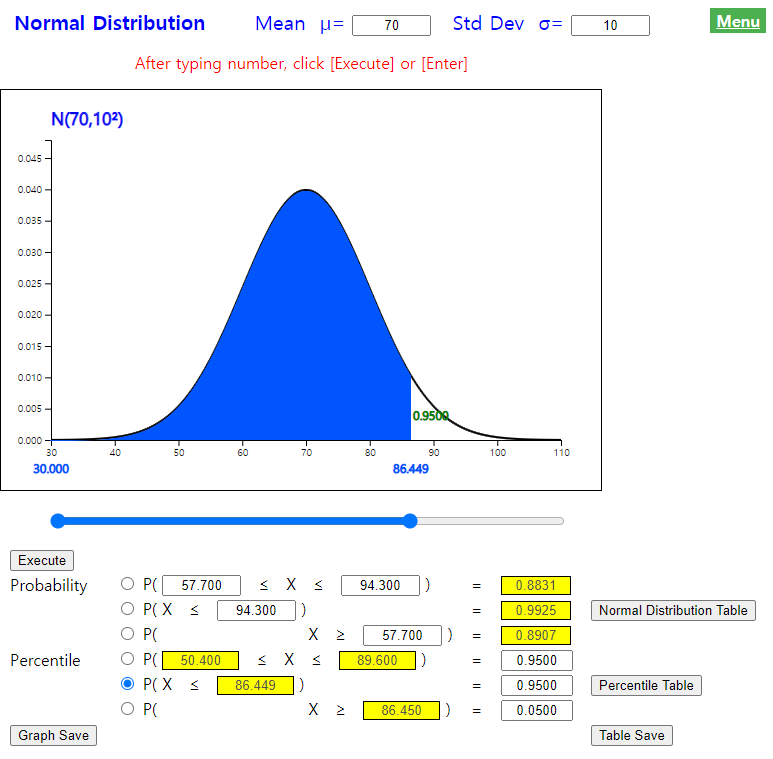
For 2), enter 0.95 at the box of the fourth option below the graph and click the [Execute] button to display the two-sided 95 percentile as (50.400, 89.600).
4.3 Multivariate distribution
4.3.1 Multivariate normal distribution
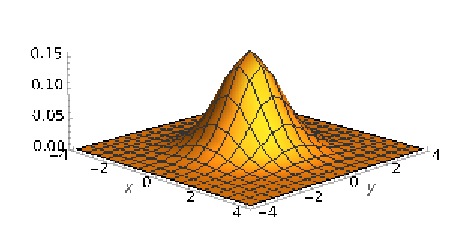
As ρ increases, the bell-shaped curve becomes flattened on the 45-degree line. So for \(\rho\) = 0.5, <Figure 4.3.2>, the curve extends towards minus 4 and plus 4 and becomes flattened in the perpendicular direction.
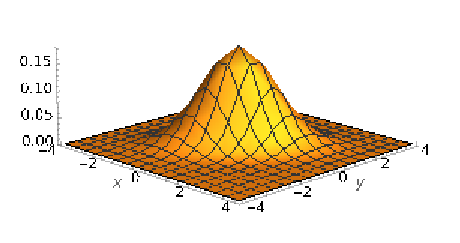
If \(\rho\) is increased to 0.9, <Figure 4.3.3>, the curve becomes broader, and the 45-degree line and even flatter in the perpendicular direction.
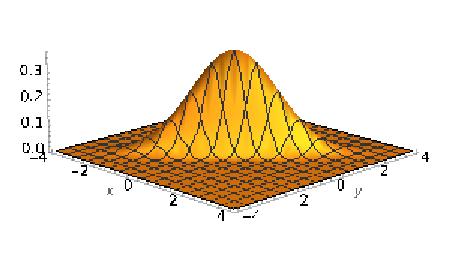
4.4 Estimation of a distribution
If univariate sample data \( {x}_1 , {x}_2 , ... , {x}_n \) follow a normal distribution \(N(\mu , \sigma^2 )\), the estimated parameters for \(\mu\) and \(\sigma^2\) using the maximum likelihood method can be shown as follows. $$ \begin{align} \hat \mu &= \frac{1}{n} \sum_{i=1}^{n} x_i \\ \hat \sigma^2 &= \frac{1}{n} \sum_{i=1}^{n} (x_i - \overline x )^2 \end{align} $$ When multivariate sample data \( {\boldsymbol x}_1 , {\boldsymbol x}_2 , ... , {\boldsymbol x}_n \) follow a multivariate normal distribution \(N(\boldsymbol \mu , \boldsymbol \Sigma )\), the estimated parameters \(\boldsymbol \mu\) and \(\boldsymbol \Sigma\) using the maximum likelihood method can be shown as follows. $$ \begin{align} \hat {\boldsymbol \mu } &= \frac{1}{n} \sum_{i=1}^{n} {\boldsymbol x}_i \\ \hat {\boldsymbol \Sigma} &= \frac{n-1}{n} \boldsymbol S \end{align} $$ where \(\boldsymbol S\) is the sample covariance matrix.
4.5 Exercise
4.1 Two executive positions in a company are vacant. Seven men and three women are fully qualified and equally eligible. The company decided to pick two of these ten people at random. Find the following odds.
4.2 300 households live in a neighborhood. One hundred are said to be out of the house in the evening. Of the remaining households, 50 do not respond to telephone surveys. When a person randomly selects a household in the neighborhood and conducts a telephone survey, ask for the following odds.
4.3 A department store surveyed 80 customers about their purchasing habits and asked, 'How many times did you buy at this department store last month?' The answer to the question is as follows.
| \(\small X\)(Number of purchases) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Number of customers | 15 | 27 | 14 | 12 | 6 | 4 | 1 | 1 |
4.4 In a factory, four machines (A, B, C, and D) are used to produce products. Machine A produces 30% of all products, machine B produces 30%, machine C produces 20%, and machine D produces 20%. The defective rates for each machine are 5%, 3%, 1%, and 1%, respectively. One day, one of the products produced was found to be defective. Find the probability that this product came from machine A, B, C, and D.
4.5 If a random variable \(\small X\) follows a binomial distribution with \(n = 6, p = 0.2\), find the following probabilities using 『eStatU』.
4.6 Over the years, a salesperson found that there was a 50% chance of selling the product when a customer visited. If five customers visit this salesman one day, calculate the following odds. Check the calculation using 『eStatU』.
4.7 It is said that 72% of drivers usually use a seat belt. When you select randomly 15 drivers, calculate the following probabilities of drivers who use a seat belt and check the calculation using 『eStatU』.
4.8 If \(\small Z\) is the standard normal random variable, obtain the following and check the calculation using 『eStatU』.
4.9 It is said that the weight of a melon follows a normal distribution with an average of 250g and standard deviation of 12g. Find the probability that the weight of the melon is less than 260 grams. Check the calculation using 『eStatU』.
4.10 4.10 A bank employee found that a customer's waiting time to receive a service follows a normal distribution with an average of 3 minutes and a standard deviation of 1 minute. Calculate the following probabilities and check the calculation using 『eStatU』.
4.11 It takes an average of 10 minutes for a production worker to finish a job at a factory, and the time follows a normal distribution with a standard deviation of 3 minutes. Calculate the following probabilities and check the calculation using 『eStatU』.