Chapter 11. Testing Hypothesis for Categorical Data

[book]    [eStat YouTube Channel]

CHAPTER OBJECTIVES

The hypothesis tests that we have studied from Chapter 7 to Chapter 10 are for continuous data. In this chapter, we describe testing hypothesis for categorical data. Section 11.1 describes the goodness of fit test for the frequency table of categorical data. Section 11.2 describes the independence and homogeneity tests for the contingence table of two categorical data.

11.1 Goodness of Fit Test

[presentation]    [video]

The frequency table of categorical data discussed in Chapter 4 counts the frequency of possible values of a categorical variable. If this frequency table is for sample data from a population, we are curious what would be the frequency distribution of the population. The goodness of fit test is a test on the hypothesis that the population follows a particular distribution based on the sample frequency distribution. In this section, we discuss the goodness of fit test for categorical distributions (Section 11.1.1) and the goodness of fit test for continuous distribution (Section 11.1.2).

11.1.1 Goodness of Fit Test for Categorical Distribution

Consider the goodness of fit test for a categorical distribution using the example below.

Example 11.1.1 The result of a survey of 150 people before a local election to find out the approval ratings of three candidates is as follows. Looking at this frequency table alone, it seems that A candidate has a 40 percent approval rating, higher than the other candidates. Based on this sample survey, perform the goodness of fit test whether three candidates have the same approval rating or not. Use 『eStatU』 with the 5% significance level.

Table 11.1.1 Frequency table of survey result in an election.

Candidate Number of Supporters Percent
A 60 40.0％
B 50 33.3％
C 40 25.7％
Total 150 100.0%

Answer

Assume each of candidate A, B, and C’s approval rating is \(p_1 , p_2 , p_3\) respectively. The hypothesis for this problem is as follows:

\(\small H_0\) : The three candidates have the same approval rating. (i.e.,\(p_1 = p_2 = p_3 = \frac{1}{3}\) )
\(\small H_1\) : The three candidates have different approval ratings.

If the null hypothesis \(\small H_0\) is true that the three candidates have the same approval rating, each candidate will have 50 (= 150\(\times \frac{1}{3}\) ) supporters out of total 150 people. It is referred to as the ‘expected frequency’ of each candidate when \(\small H_0\) is true. For each candidate, the number of observed supporters in the sample is called the 'observed frequency'. If \(\small H_0\) is true, the observed and expected number of supporters can be summarized as the following table.

Candidate Observed frequency
(denoted as \(O_i\))		 Expected frequency
(denoted as \(E_i\))
A \(O_1 = 60\) \(E_1 = 50\)
B \(O_2 = 50\) \(E_2 = 50\)
C \(O_3 = 40\) \(E_3 = 50\)
Total 150 150

If \(\small H_0\) is true, the observed frequency (\(\small O_i\)) and the expected frequency (\(\small E_i\)) will coincide. Therefore, in order to test the hypothesis, a statistic which uses the squared difference between \(\small O_i\) and \(\small E_i\) is used. Specifically, the statistic to test the hypotheses is as follows:

\( {\chi}_{obs}^2 = \frac {(O_1 - E_1 )^2} {E_1} + \frac {(O_2 - E_2 ) ^2} {E_2} + \frac {(O_3 - E_3 )^2} {E_3} \)

If the observed value of this test statistic is close to zero, it can be considered that \(\small H_0\) is true, because \(\small O_i\) is close to \(\small E_i\). If the observed value is large, \(\small H_0\) will be rejected. The question is, 'How large value of the test statistic would be considered as the statistically significant one?' It can be shown that this test statistic approximately follows the chi-square distribution with \(k-1\) degrees of freedom if the expected frequency is large enough. Here \(k\) is the number of categories (i.e., candidates) in the table and it is 3 in this example. Therefore, the decision rule to test the hypotheses is as follows:

‘If \(\chi_{obs}^2 > \chi_{k-1; α}^2\) , reject \(\small H_0\), else do not reject \(\small H_0\)’

The statistic \(\chi_{obs}^2\) can be calculated as follows:

\( {\chi}_{obs}^2 = \frac {(60 - 50)^2} {50} + \frac {(50 - 50 ) ^2} {50} + \frac {(40 - 50)^2} {50}\)

Since the significance level α is 5％, the critical value can be found from the chi-square distribution as follows:

\( \chi_{k-1 ; α}^{2} = \chi_{3-1 ; 0.05}^{2} = \chi_{2 ; 0.05}^{2} = 5.991 \)

Therefore, \(\small H_0\) cannot be rejected. In other words, although the above sample frequency table shows that the approval ratings of the three candidates differ, this difference does not provide sufficient evidence to conclude that the three candidates have different approval ratings.

Since sample approval ratings of each candidate are \(\hat p_1 = \frac{60}{150}\) = 0.40, \(\hat p_2 = \frac{50}{150}\) = 0.33, \(\hat p_3 = \frac{40}{150}\) = 0.27, the 95% confidence intervals for the population proportion of each candidate's approval rating using the formula (\( {{\hat p}} ± 1.96 \sqrt { \hat p (1- \hat p ) / n } \)) (refer Chapter 6.4) are as follows:

A: \( \quad 0.40 \pm 1.96 \sqrt { \frac {0.40 \times 0.60} {150} } \quad \quad \Leftrightarrow \quad \) [0.322, 0.478]
B: \( \quad 0.33 \pm 1.96 \sqrt { \frac {0.33 \times 0.67} {150} } \quad \quad \Leftrightarrow \quad \) [0.255, 0.405]
C: \( \quad 0.27 \pm 1.96 \sqrt { \frac {0.27 \times 0.73} {150} } \quad \quad \Leftrightarrow \quad \) [0.190, 0.330]

The overlapping of the confidence intervals on the three candidates' approval ratings means that one candidate's approval rating is not completely different from the other.

In the data input box that appears by selecting the [Goodness of Fit Test] of 『eStatU』, enter the 'Observed Frequency' and 'Expected Probability' data as shown in <Figure 11.1.1>. After entering the data, select the significance level and click [Execute] button to calculate the 'Expected Frequency' and to see the result of the chi-square test. Be sure that this chi-square goodness of fit test should be applied when the expected frequency of each category is at least 5.

[]

<Figure 11.1.2> 『eStatU』 Chi-square Goodness of Fit Test

Consider a categorical variable X which has \(k\) number of possible values \(x_1 , x_2 , ... , x_k\) and their probabilities are \(p_1 , p_2 , ... , p_k\) respectively. In other words, the probability distribution for the categorical variable X is as follows:

\(X\) \(P(X = x)\)
\(x_1\) \(p_1\)
\(x_2\) \(p_2\)
\(\cdots\) \(\cdots\)
\(x_k\) \(p_k\)
Total 1

When random samples are collected from the population of the categorical random variable X and their observed frequencies are (\(O_1 , O_2 , ... , O_k \)), the hypothesis to test the population probability distribution of (\(p_1 , p_2 , ... , p_k \)) = (\(p_{10} , p_{20} , ... , p_{k0} \)) is as follows:

\(\qquad H_0\) : Distribution of (\(O_1 , O_2 , ... , O_k \)) are from the distribution (\(p_1 , p_2 , ... , p_k \)) = (\(p_{10} , p_{20} , ... , p_{k0} ) \)
\(\qquad H_1\) : Distribution of (\(O_1 , O_2 , ... , O_k \)) are not from the distribution (\(p_1 , p_2 , ... , p_k \)) = (\(p_{10} , p_{20} , ... , p_{k0} ) \)

If the total number of samples \(n\) is large enough, the above hypothesis can be tested using the following chi-square test statistic as follows: $$ \text{‘If } \chi_{obs}^{2} = \sum_{i=1}^{k} \frac { (O_{i} - E_{i} )^{2}} {E_{i}} > \chi_{k-m-1 ; α}^{2}, \text{ then reject } H_0 ’ $$ Here, (\(E_1 , E_2 , ... , E_k \)) = (\(np_{10} , np_{20} , ... , np_{k0} \)) are expected frequencies, \(m\) is the number of population parameters estimated from the sample data. In [Example 11.1.1], since there was not a population parameter estimated from the sample, \(m\) = 0 .

Goodness of Fit Test

Consider a categorical variable \(X\) which has \(k\) number of possible values \(x_1 , x_2 , ... , x_k \) and there probabilities are \(p_1 , p_2 , ... , p_k \) respectively. Let observed frequencies for each value of \(X\) from \(n\) samples are (\(O_1 , O_2 , ... , O_k \)), expected frequencies for each value of \(X\) from \(n\) samples are \( ( E_1 , E_2 , ... , E_k )\) = \((np_{10} , np_{20} , ... , np_{k0} ) \) and the significance level is α.

Hypothesis:

\(H_0\) : Distribution of (\(O_1 , O_2 , ... , O_k \)) follows \( (p_{10} , p_{20} , ... , p_{k0} )\)
\(H_1\) : Distribution of (\(O_1 , O_2 , ... , O_k \)) does not follow \((p_{10} , p_{20} , ... , p_{k0} )\)

Decision Rule:

‘If \( \chi_{obs}^{2} = \sum_{i=1}^{k} \frac { (O_{i} - E_{i} )^{2}} {E_{i}} > \chi_{k-m-1 ; α}^{2}\), then reject \(H_0\) ’
where \(m\) is the number of population parameters estimated from the samples.

\(\clubsuit\) In order to use the chi-square Goodness of Fit test, all expected frequencies \(E_i\) should be greater than 5.

\(\clubsuit\) A category which has an expected frequency less than 5 can be merged with other category.

Practice 11.1.1 Market shares of toothpaste A, B, C and D are known to be 0.3, 0.6, 0.08, and 0.02 respectively. The result of a survey of 100 people for the toothpaste brands are as follows. Can you conclude from these data that the known market share is incorrect? Use 『eStatU』. \(\alpha\) = 0.05.

Brand Number of Customers
A 192
B 342
C 44
D 22
Total600

11.1.2 Goodness of Fit Test for Continuous Distribution

[presentation]    [video]

The goodness of fit test for categorical data using the chi-square distribution can also be used for continuous data. The following is an example of the goodness of fit test in which data are derived from a population of a normal distribution. The parametric statistical tests from Chapter 6 to Chapter 9 require the assumption that the population is normally distributed and the goodness of fit test in this section can be used to test for normality.

Example 11.1.2 Ages of 30 people who visited a library in the morning are as follows. Test the hypothesis that the population is normally distributed at the significance level of 5%.

28 55 26 35 43 47 47 17 35 36 48 47 34 28 43
20 30 53 27 32 34 43 18 38 29 44 67 48 45 43
[Ex] ⇨ eBook ⇨ EX110102_AgeOfLibraryVisitor.csv

Answer

Age is a continuous variable, but you can make a frequency distribution by dividing possible values into intervals as we studied in histogram of Chapter 3. It is called a categorization of the continuous data.

Let's find a frequency table which starts at the age of 10 with the interval size of 10. The histogram of 『eStat』 makes this frequency table easy to obtain.

If you enter the data as shown in <Figure 11.1.3>, click the histogram icon and select Age from the variable selection box, then the histogram as <Figure 11.1.4> will appear.

<Figure 11.1.3> Data input at 『eStat』

<Figure 11.1.4> Default histogram of age

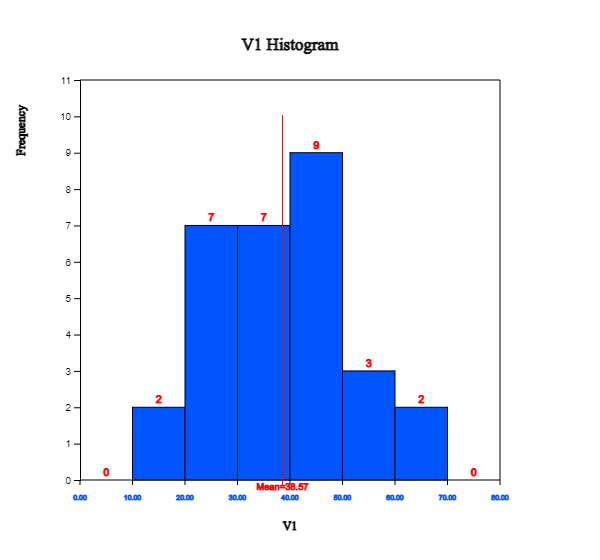
If you specify 'start interval' as 10 and 'interval width' as 10 in the options window below the histogram, the histogram of <Figure 11.1.4> is adjusted as <Figure 11.1.5>. If you click [Frequency Table] button, the frequency table as shown in <Figure 11.1.6> will appear in the Log Area. The designation of interval size can be determined by a researcher.

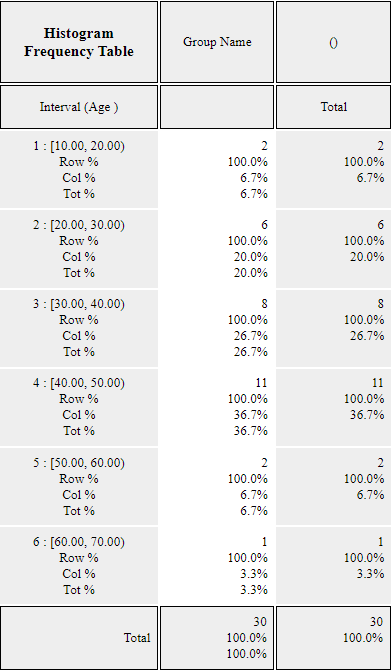
<Figure 11.1.5> Adjusted histogram of age

<Figure 11.1.6> Frequency table of the adjusted histogram

Since the normal distribution is a continuous distribution defined at \(-\infty \lt x \lt \infty\) , the frequency table of <Figure 11.1.6> can be written as follows:

Table 11.1.2 Frequency table of age with adjusted interval

Interval id Interval Observed frequency
1 \( X < 20 \) 2
2 \(20 \le X < 30\) 6
3 \(30 \le X < 40\) 8
4 \(40 \le X < 50\) 11
5 \(50 \le X < 60\) 2
6 \( X \ge 60 \) 1

The frequency table of sample data as Table 11.1.2 can be used to test the goodness of fit whether the sample data follows a normal distribution using the chi-square distribution. The hypothesis of this problem is as follows:

\(\small H_0\): Sample data follows a normal distribution
\(\small H_1\): Sample data does not follow a normal distribution

This hypothesis does not specify what a normal distribution is and therefore, the population mean \(\mu\) and the population variance \(\sigma^2\) should be estimated from sample data. Pressing the 'Basic Statistics' icon on the main menu of 『eStat』 will display a table of basic statistics in the Log Area, as shown in <Figure 11.1.7>. The sample mean is 38.000 and the sample standard deviation is 11.519.

<Figure 11.1.7> Descriptive statistics of age

Hence, the above hypothesis can be written in detail as follows:

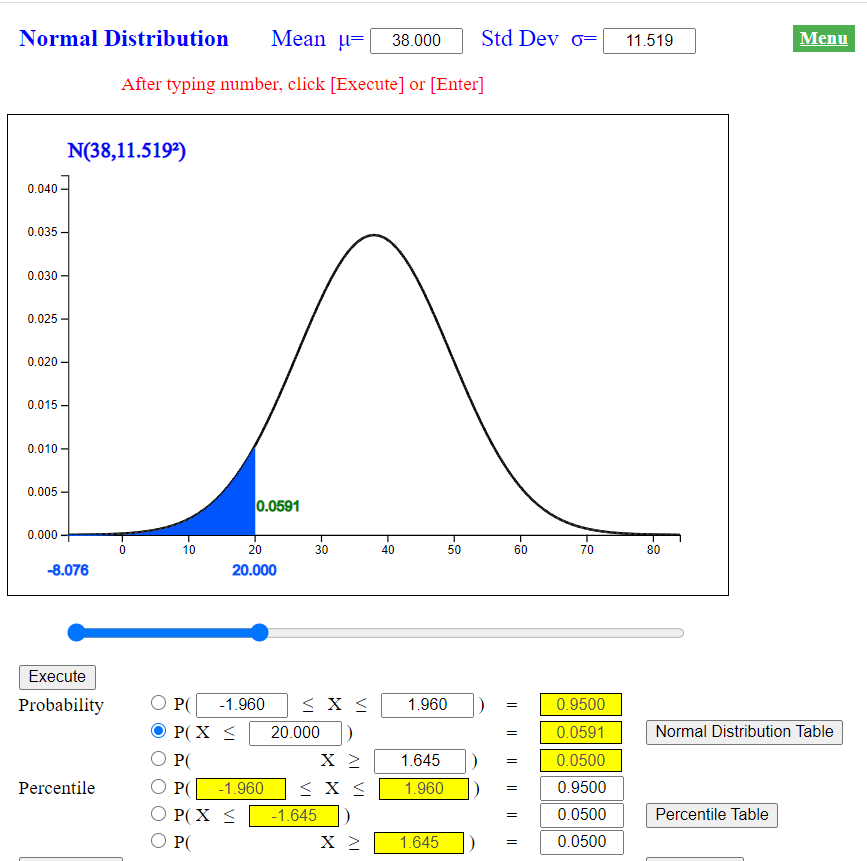
\(\small H_0\): Sample data follows \(N(38.000, 11.519^2 )\)
\(\small H_1\): Sample data does not follow \(N(38.000, 11.519^2 )\)

In order to find the expected frequency of each interval when \(\small H_0\) is true, the expected probability of each interval is calculated first using the normal distribution \(\small N(38.000, 11.519^2 )\) as follows. The normal distribution module of 『eStatU』 makes it easy to calculate this probability of an interval. At the normal distribution module of 『eStatU』, enter the mean of 38.000 and the standard deviation of 11.519. Click the second radio button of P(X < x) type and enter 20, then press the [Execute] button to calculate the probability as shown in <Figure 11.1.8>.

\(P(X \lt 20) = P(Z \lt \frac {20-38.000} {11.519} ) = P(Z \lt -1.563)=0.059\)

<Figure 11.1.8> Calculation of normal probability using 『eStatU』

Similarly you can calculate the following probabilities.

\(P(20 \le X \lt 30) = P(\frac{20-38.000}{11.519} \le Z \lt \frac {30-38.000}{11.519} ) = P(-1.563 \le Z \lt -0.695) = 0.185\)
\(P(30 \le X \lt 40) = P(\frac{30-38.000}{11.519} \le Z \lt \frac {40-38.000}{11.519} ) = P(-0.695 \le Z \lt 0.174) = 0.325\)
\(P(40 \le X \lt 50) = P(\frac{40-38.000}{11.519} \le Z \lt \frac {50-38.000}{11.519} ) = P( 0.174 \le Z \lt 1.042) = 0.282\)
\(P(50 \le X \lt 60) = P(\frac{50-38.000}{11.519} \le Z \lt \frac {60-38.000}{11.519} ) = P( 1.042 \le Z \lt 1.910) = 0.121\)
\(P( X \ge 60) = P( Z \ge \frac {60-38.000}{11.519} ) = P( Z \ge 1.910) = 0.028\)

Expected frequency can be calculated by multiplying the sample size of 30 to the expected probability of each interval obtained above. The observed frequencies, expected probabilities, and expected frequencies for each interval can be summarized as the following table.

Table 11.1.3 Observed and expected frequencies of each interval of distribution

Interval id Interval Observed frequency Expected probability Expected frequency
1 \( X < 20 \) 2 0.059 1.77
2 \(20 \le X < 30\) 6 0.185 5.55
3 \(30 \le X < 40\) 8 0.325 9.75
4 \(40 \le X < 50\) 12 0.282 8.46
5 \(50 \le X < 60\) 2 0.121 3.63
6 \( X \ge 60 \) 1 0.028 0.84

Since the expected frequencies of the 1st and 6th interval are less than 5, the intervals should be combined with adjacent intervals for testing the goodness of fit using the chi-square distribution as Table 11.1.4. The expected frequency of the last interval is still less than 5, but, if we combine this interval, there are only three intervals, we demonstrate the calculation as it is. Note that, due to computational error, the sum of the expected probabilities may not be exactly equal to 1 and the sum of the expected frequencies may not be exactly 30 in Table 11.1.4.

Table 11.1.4 Revised table after combining interval of small expected frequency

Interval id Interval Observed frequency Expected probability Expected frequency
1 \( X < 30 \) 8 0.244 7.32
2 \(30 \le X < 40\) 8 0.325 9.75
3 \(40 \le X < 50\) 11 0.282 8.48
4 \( X \ge 50 \) 3 0.149 4.47
Total 30 1.000 30.00

The test statistic for the goodness of fit test is as follows:

\(\chi_{obs}^{2} = \frac{(8-7.32)^{2}}{7.32} + \frac{(8-9.75)^{2}}{9.75} + \frac{(11-8.48)^{2}}{8.48} + \frac{(3-4.47)^{2}}{4.47} = 1.623\)

Since the number of intervals is 4, \(k\) becomes 4, and \(m\)=2, because two population parameters \(\mu\) and \(\sigma^2\) are estimated from the sample data. Therefore, the critical value is as follows:

\(\chi_{k-m-1; α}^{2} = \chi_{4-2-1; 0.05}^{2} = \chi_{1; 0.05}^{2} = 3.841\)

The observed test statistic is less than the critical value, we can not reject the null hypothesis that the sample data follows \(\small N(38.000, 11.519^2 )\) .

Test result can be verified using [Categorical: Goodness of Fit Test] in 『eStatU』. In the Input box that appears by selecting the module, enter the data for 'Observed Frequency' and 'Expected Probability' in Table 11.1.4, as shown in <Figure 11.1.9>. After entering the data, select the significance level and press the [Execute] button to calculate the 'expected frequency' and produce a chi-square test result as in <Figure 11.1.10>.

[]

<Figure 11.1.10> Chi-square goodness of fit test using 『eStatU』

Practice 11.1.2 (Otter length)
Data of 30 otter lengths can be found at the following location of 『eStat』.

[Ex] ⇨ eBook ⇨ PR110102_OtterLength.csv

Test the hypothesis that the population is normally distributed at the significance level of 5% using 『eStat』.

11.2 Testing Hypothesis for Contingency Table

[presentation]    [video]

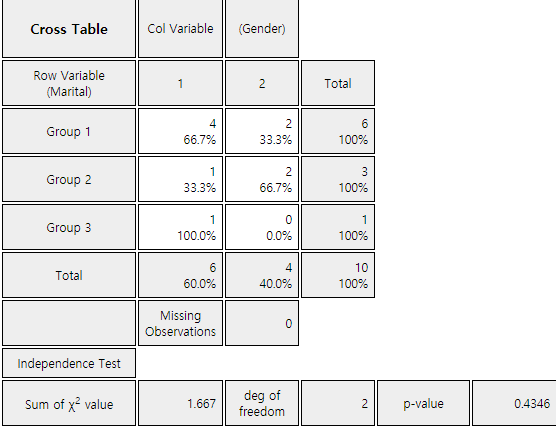
The contingency table or cross table discussed in Chapter 4 was a table that placed the possible values of two categorical variables in rows and columns, respectively, and examined frequencies of each cell in which the values of the two variables intersect. If this contingency table is for sample data taken from a population, it is possible to predict what would be the contingency table of the population. The test for the contingency table is usually an analysis of the relation between two categorical variables and it can be divided into the independence test and homogeneity test according to the sampling method for obtaining the data.

11.2.1 Independence Test

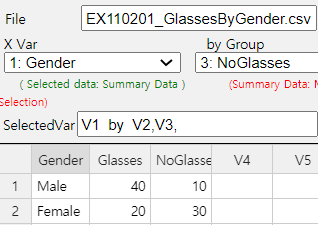
The independence test of the contingency table is to investigate whether two categorical variables are independent when samples are extracted from one population. Consider the independence test with the following example.

Example 11.2.1 In order to investigate whether college students who are wearing glasses are independent by gender, a sample of 100 students was collected and its contingency table was prepared as follows:

Table 11.2.1 Wearing glasses by gender

Wear Glasses No Glasses Total
Men 40 10 50
Women 20 30 50
Total 60 40 100

[Ex] ⇨ eBook ⇨ EX110201_GlassesByGender.csv.

1) Using 『eStat』, draw a line graph of the use of eyeglasses by men and women.
2) Test the hypothesis at 5% of the significance level to see if the gender variable and the wearing of glasses are independent or related to each other.
3) Check the result of the independence test using 『eStatU』.

Answer

1) Enter data in 『eStat』 as shown in <Figure 11.2.1>.

<Figure 11.2.1> Data input

Select 'Line Graph' icon from the main menu. If you click variables ‘Gender’, ‘Glasses’, ‘NoGlasses’ one by one, then a line graph as shown in <Figure 11.2.2> will appear in the Graph Area. If you look at the line graph, you can see that the ratio of wearing glasses for men and women are different. For men, there are many male students who wear glasses (80% of men) and many female students who do not wear glasses (60% of women). In such cases, the gender variable and the wearing of glasses are considered related. As such, when two variables are related, two lines of the line graph intersect to each other.

<Figure 11.2.2> Line graph of wearing glasses by gender

2) If two variables are not related (i.e., if the two variables are independent of each other), the contingency table in Table 11.2.1 will show that the proportion of wearing glasses by men or women is equal to 60% which is the proportion of all students wearing glasses. In other words, if two variables are independent, the contingency table should be as follows:

Table 11.2.2 Contingency table when gender and wearing glasses are independent

Wear Glasses No Glasses Total
Men 30 20 50
Women 30 20 50
Total 60 40 100

If there is little difference between the observed contingency table and the contingency table in the case of independence, two categorical variables are said to be independent of each other. If the differences are very large, two categorical variables are related to each other. The independence test is a statistical method for determining that two categorical variables of the population are independent of each other by using the observed contingency table obtained from the sample. The independent test uses the chi-square distribution and the hypothesis is as follows:

\(\small H_0 :\) Two variables of the contingency table are independent of each other.
\(\small H_1 :\) Two variables of the contingency table are related.

The test statistic for testing this hypothesis utilizes the difference between the observed frequency of the contingency table in the sample and the expected frequency of the contingency table when two variables are assumed to be independent which is similar to the goodness of fit test. The test statistic in this example is as follows:

\(\chi_{obs}^{2~} = \frac{(40-30)^{2}}{30} + \frac{(10-20)^{2}}{20} + \frac{(20-30)^{2}}{30} + \frac{(30-20)^{2}}{20} \) = 16.67

This test statistic follows a chi-square distribution with \((r-1)(c-1)\) degrees of freedom where \(r\) is the number of rows (number of possible values of row variable) and \(c\) is the number of columns (number of possible values of column variable). Therefore, the decision rule to test the hypothesis is as follows:

'If \(\chi_{obs}^{2} > \chi_{(r-1)(c-1); α}^{2}\), then reject \(\small H_0\).'

In this example, \(\chi_{obs}^{2}\) = 16.67 is greater than the critical value \(\chi_{(r-1)(c-1); α}^{2} = \chi_{(2-1)(2-1); 0.05}^{2} = \chi_{1; 0.05}^{2}\) = 3.841. Therefore, the null hypothesis that two variables are independent each other is rejected and we conclude that the gender and wearing glasses are related.

3) In 『eStatU』, click [Categorical: Independence Test]. Enter data as shown in <Figure 11.2.3> and press the [Execute] button to display the result of the chi-square test as shown in <Figure 11.2.4>.

[]

<Figure 11.2.4> 『eStatU』 Chi-square test of independence

Assume that there are \(r\) number of attributes of the variable \(A\) such as \(A_1 , A_2 , ... , A_r\) , and \(c\) number of attributes of the variable \(B\) such as \(B_1 , B_2 , ... , B_c\). Let \(p_{ij}\) denote the probability of the cell of \(A_i\) and \(B_j\) attribute in the contingency table of \(A\) and \(B\) as Table 11.2.3. Here \(p_{i\cdot} = p_{i1} + p_{i2} + \cdots + p_{ic}\) denotes the probability of \(A_i\) and \(p_{\cdot j} = p_{1j} + p_{2j} + \cdots + p_{rj}\) denotes the probability of \(B_j\).

Table 11.2.3 Notation of probabilities in \(r \times c \) contingency table

Variable A | Variable B \(B_1\) \(B_2\) \(\cdots\) \(B_c\) Total
\(A_1\) \(p_{11}\) \(p_{12}\) \(\cdots\) \(p_{1c}\) \(p_{1\cdot}\)
\(A_2\) \(p_{21}\) \(p_{22}\) \(\cdots\) \(p_{2c}\) \(p_{2\cdot}\)
\(\cdots\) \(\cdots\) \(\cdots\) \(\cdots\) \(\cdots\) \(\cdots\)
\(A_r\) \(p_{r1}\) \(p_{r2}\) \(\cdots\) \(p_{rc}\) \(p_{r\cdot}\)
Total \(p_{\cdot 1}\) \(p_{\cdot 2}\) \(\cdots\) \(p_{\cdot c}\) 1

If two events \(A_i\) and \(B_j\) are independent, \(P(A_{i} \cap B_{j} ) = P(A_{i})·P(B_{j} ) \) and hence, \(p_{ij} = p_{i \cdot} p_{\cdot j} \). If two variables \(A\) and \(B\) are independent, all \(A_i\) and \(B_j\) should satisfy the above property which is called the independent test.

\(H_0 :\) Variable \(A\) and \(B\) are independent.
\(H_1 :\) Variable \(A\) and \(B\) are not independent.

In order to test whether two variables of the population are independent, let us assume the observed frequencies, \(O_{ij}\)'s, of the contingency table from \(n\) samples are as follows:

Table 11.2.4 Observed frequency of contingency table

Variable A | Variable B \(B_1\) \(B_2\) \(\cdots\) \(B_c\) Total
\(A_1\) \(O_{11}\) \(O_{12}\) \(\cdots\) \(O_{1c}\) \(T_{1\cdot}\)
\(A_2\) \(O_{21}\) \(O_{22}\) \(\cdots\) \(O_{2c}\) \(T_{2\cdot}\)
\(\cdots\) \(\cdots\) \(\cdots\) \(\cdots\) \(\cdots\) \(\cdots\)
\(A_r\) \(O_{r1}\) \(O_{r2}\) \(\cdots\) \(O_{rc}\) \(T_{r\cdot}\)
Total \(T_{\cdot 1}\) \(T_{\cdot 2}\) \(\cdots\) \(T_{\cdot c}\) n

If the null hypothesis \(H_0 :\) is true, i.e., if two variables are independent of each other, the expected frequency of the sample data will be \(n p_{i \cdot} p_{\cdot j} \). Since we do not know the population \(p_i\) and \(p_j\), if we use the estimates of \(\frac {T_{i \cdot}}{n} \) and \(\frac {T_{\cdot j}}{n} \), then the estimate of the expected frequency, \(E_{ij} \), is as follows: $$ E_{ij} = n( \frac {T_{i\cdot}} {n} )( \frac {T_{\cdot j}} {n} ) = T_{i\cdot} ( \frac {T_{\cdot j}} {n} ) $$ The expected frequencies in case of independent can be explained that the proportions of each attribute of the B variable, \(( \frac {T_{\cdot 1}} {n}, \frac {T_{\cdot 2}} {n}, ... , \frac {T_{\cdot r}} {n} )\), are maintained in each attribute of the \(A\) variable.

Table 11.2.5 Expected frequency of contingency table

Variable A \ Variable B \(B_1\) \(B_2\) \(\cdots\) \(B_c\)
\(A_1\) \(E_{11} = T_{1\cdot} \times \frac {T_{\cdot 1}}{n}\) \(E_{12} = T_{1\cdot} \times \frac {T_{\cdot 2}}{n}\) \(\cdots\) \(E_{1c} = T_{1\cdot} \times \frac {T_{\cdot c}}{n}\)
\(A_2\) \(E_{21} = T_{2\cdot} \times \frac {T_{\cdot 1}}{n}\) \(E_{22} = T_{2\cdot} \times \frac {T_{\cdot 2}}{n}\) \(\cdots\) \(E_{2c} = T_{2\cdot} \times \frac {T_{\cdot c}}{n}\)
\(\cdots\) \(\cdots\) \(\cdots\) \(\cdots\) \(\cdots\)
\(A_r\) \(E_{r1} = T_{r\cdot} \times \frac {T_{\cdot 1}}{n}\) \(E_{r2} = T_{r\cdot} \times \frac {T_{\cdot 2}}{n}\) \(\cdots\) \(E_{rc} = T_{r\cdot} \times \frac {T_{\cdot c}}{n}\)

The test statistic utilizes the difference between \(O_{ij}\) and \(E_{ij}\) as follows: $$ \sum_{i=1}^{r} \sum_{j=1}^{c} \frac {(O_{ij} - E_{ij} )^2} {E_{ij}} $$

This test statistic follows approximately a chi-square distribution with \((r-1)(c-1)\) degrees of freedom. Therefore, the decision rule to test the hypothesis with significance level of \(\alpha\) is as follows: $$ \text{'If}\quad \chi_{obs}^2 = \sum_{i=1}^{r} \sum_{j=1}^{c} \frac {(O_{ij} - E_{ij} )^2} {E_{ij}} \gt \chi_{(r-1)(c-1); α}^2,\; \text{then reject}\;\; H_0' $$

Independence Test

Hypothesis:

\(H_0 :\) Variable \(A\) and \(B\) are independent.
      i.e., \(p_{ij} = p_{i·} \cdot p_{·j}, i=1,2, ... , r, \;\; j=1,2, ... , c\)
\(H_1 :\) Variable \(A\) and \(B\) are not independent.

Decision Rule:
$$ \text{‘If}\quad \chi_{obs}^2 = \sum_{i=1}^{r} \sum_{j=1}^{c} \frac {(O_{ij} - E_{ij} )^2} {E_{ij}} \gt \chi_{(r-1)(c-1); α}^2,\; \text{then reject}\;\; H_0 ’ $$ where \(r\) is the number of attributes of row variable and \(c\) is the number of attributes of column variable.

\(\clubsuit\) In order to use the chi-square distribution for the independence test, all expected frequencies are at least 5 or more.

\(\clubsuit\) If an expected frequency of a cell is smaller than 5, the cell is combined with adjacent cell for analysis.

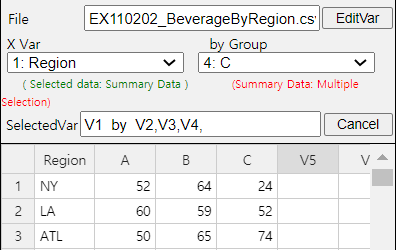
Consider an example of the independent test with many rows and columns.

Example 11.2.2 A market research institute surveyed 500 people on how three beverage products (A, B and C) are preferred by region and obtained the following contingency table.

Table 11.2.6 Survey for preference of beverage by region

Region \ Beverage A B C Total
New York 52 64 24 140
Los Angels 60 59 52 171
Atlanta 50 65 74 189
Total 162 188 150 500

[Ex] ⇨ eBook ⇨ EX110202_BeverageByRegion.csv.

1) Draw a line graph of beverage preference by region using 『eStat』 and analyze the graph.
2) Test whether the beverage preference by the region is independent of each other at the significance level of 5%.
3) Check the result of the independence test using 『eStatU』.

Answer

1) Enter the data in 『eStat』 as shown in <Figure 11.2.5>.

<Figure 11.2.5> Data input

Select 'Line Graph' and click variables ‘Region’, ‘A’, ‘B’, and ‘C’ in order, then the line graph shown in <Figure 11.2.6> will appear. If you look at the line graph, you can see the cross-section of the lines from region to region, and the regional preference is different. Can you statistically conclude that the region and beverage preference are related?

<Figure 11.2.6> Line graph by region and beverage

2) The hypothesis for the independence test is as follows:

\(\small\qquad H_0\): Region and beverage preference are independent.
\(\small\qquad H_1\): Region and beverage preference are not independent.

In order to calculate the expected frequencies, we first calculate the proportions of each beverage preference without considering the region as follows:

\(\qquad ( \frac{162}{500}, \frac{88}{500}, \frac{50}{500} )\)

If two variables are independent, these proportions should be kept in each region. Hence, the expected frequencies in each region can be calculated as follows:

\(\small\qquad E_{11} = 140 \times \frac{162}{500} = 45.36, \quad E_{12} = 140 \times \frac{188}{500} = 52.64, \quad E_{13} = 140 \times \frac{150}{500} = 42.00\) \(\small\qquad E_{21} = 171 \times \frac{162}{500} = 55.40, \quad E_{22} = 171 \times \frac{188}{500} = 64.30, \quad E_{23} = 171 \times \frac{150}{500} = 51.30\) \(\small\qquad E_{31} = 189 \times \frac{162}{500} = 61.24, \quad E_{32} = 189 \times \frac{188}{500} = 71.06, \quad E_{33} = 189 \times \frac{150}{500} = 56.70\)

The chi-square test statistic and critical value are as follows:

\(\qquad \chi_{obs}^2 = \sum_{i=1}^3 \sum_{j=1}^3 \; \frac{(O_{ij} - E_{ij} )^2 }{E_{ij}} = \frac{(52 -45.36)^2}{45.36} + \frac{(60-55.40)^2}{55.40} + \cdots + \frac{(74-56.70)^2}{56.70} \) = 19.822

\(\qquad \chi_{(r-1)(c-1); α}^2 = \chi_{(3-1)(3-1); 0.05}^2 = \chi_{4; 0.05}^2 \) = 9.488

Therefore, the null hypothesis \(\small H_0\) is rejected at the significance level of 5％ and conclude that the region and beverage are related.

3) In the independence test of 『eStatU』, enter data as shown in <Figure 11.2.7> and click the [Execute] button to display the result of the chi-square test as shown in <Figure 11.2.8>.

[]

<Figure 11.2.8> Chi-square Independence Test at 『eStatU』

As described in Chapter 4, if a contingency table is made using raw data (<Figure 11.2.9>), 『eStat』 provides the result of the independence test as shown in <Figure 11.2.10>. In this case, if a cell of the contingency table has a small expected number, the test result should be interpreted carefully.

<Figure 11.2.9> Raw data input for independence test

<Figure 11.2.10> 『eStat』 contingency table and independence test

Practice 11.2.1 A guidance counselor surveyed 100 high school students for reading and watching TV. The following table was obtained by classifying each item as high and low. Using the significance level of 0.05, are these data sufficient to claim that the reading and TV viewing are related? Check the test result using 『eStatU』.

TV View \ Reading High Low Total
High 40 18 58
Low 31 11 42
Total 71 29 100

[Ex] ⇨ eBook ⇨ EX110201_TV_Reading.csv.

11.2.2 Homogeneity Test

[presentation]    [video]

The independence test described in the previous section were for the contingency table of two categorical variables based on sample data from one population. However, similar contingency table may be taken from several populations, where each sample is drawn from such a different population. It can often be seen when the research is more efficiently to be done or when time and space constraints are imposed. For example, if you want to compare the English scores of freshman, sophomore, junior and senior students in a university, it is reasonable to take samples from each grade and analyze them. In this case, the contingency table is as follows:

Table 11.2.7 A contingency table of English score by grade level

Score \ Grade Freshman Sophomore Junior Senior
A - - - -
B - - - -
C - - - -
D - - - -

If this contingency table is derived from each grade population, the question we are curious is not an independence of the English score and grade level, but four distributions of English scores are equal. The hypothesis for a contingency table of samples drawn from multiple populations is as follows. It is called the homogeneity test.

\(\qquad H_0\): Distributions of several populations for a categorical variable are homogeneous.
\(\qquad H_1\): Distributions of several populations for a categorical variable are not homogeneous.

The test statistic for the homogeneity test is the same as the independence test as follows: $$ \chi_{obs}^2 = \sum_{i=1}^{r} \sum_{j=1}^{c} \frac {(O_{ij} - E_{ij} )^2} {E_{ij}} $$ Here \(r\) is the number of attributes of row variable and \(c\) is the number of populations.

Homogeneity Test

Hypothesis:

\(H_0\): Distributions of several populations for a categorical variable are homogeneous.
\(H_1\): Distributions of several populations for a categorical variable are not homogeneous.

Decision Rule: $$ \text{‘If}\quad \chi_{obs}^2 = \sum_{i=1}^{r} \sum_{j=1}^{c} \frac {(O_{ij} - E_{ij} )^2} {E_{ij}} \gt \chi_{(r-1)(c-1); α}^2,\; \text{then reject}\;\; H_0 ’ $$ Here \(r\) is the number of attributes of row variable and \(c\) is the number of populations.

\(\clubsuit\) In order to use the chi-square distribution for the homogeneity test, all expected frequencies are at least 5 or more.

\(\clubsuit\) If an expected frequency of a cell is smaller than 5, the cell is combined with adjacent cell for analysis.

Example 11.2.3 In order to investigate whether viewers of TV programs are different by age for three programs (A, B and C), 200, 100 and 100 samples were taken separately from the population of young people(20s), middle-aged people (30s and 40s), and older people (50s and over) respectively. Their preference of the program were summarized as follows. Test whether TV program preferences vary by age group at the significance level of 5%.

Table 11.2.8 Preference of TV program by age group

TV Program \ Age Group Young Middle Aged Older Total
A 120 10 10 140
B 30 75 30 135
C 50 15 60 125
Total 200 100 100 400

Answer

The hypothesis of this problem is as follows:

\(\quad \small H_0\): TV program preferences for different age groups are homogeneous.
\(\quad \small H_1\): TV program preferences for different age groups are not homogeneous.

Proportions of the number of samples for each age group are as follows:

\(\quad ( \frac{200}{400}, \frac{100}{400}, \frac{100}{400} )\)

Therefore, the expected frequencies of each program when is true are as follows:

If two variables are independent, these proportions should be kept in each region. Hence, the expected frequencies in each region can be calculated as follows:

\(\small \quad E_{11} = 140 \times \frac{200}{400} = 70.00, \quad E_{12} = 140 \times \frac{100}{400} = 35.00, \quad E_{13} = 140 \times \frac{100}{400} = 35.00\) \(\small \quad E_{21} = 135 \times \frac{200}{400} = 67.50, \quad E_{22} = 135 \times \frac{100}{400} = 33.75, \quad E_{23} = 135 \times \frac{100}{400} = 33.75\) \(\small \quad E_{31} = 125 \times \frac{200}{400} = 62.50, \quad E_{32} = 125 \times \frac{100}{400} = 31.25, \quad E_{33} = 125 \times \frac{100}{400} = 31.25\)

The chi-square test statistic and critical value are as follows:

\(\qquad \chi_{obs}^2 = \sum_{i=1}^3 \sum_{j=1}^3 \; \frac{(O_{ij} - E_{ij} )^2 }{E_{ij}} = \frac{(120-70)^2}{70} + \frac{(10-35)^2}{35} + \cdots + \frac{(60-31.25)^2}{31.25} \) = 180.495

\(\qquad \chi_{(r-1)(c-1); α}^2 = \chi_{(3-1)(3-1); 0.05}^2 = \chi_{4; 0.05}^2 \) = 9.488

Since \(\chi_{obs}^2\) is greater than the critical value, \(\small H_0\) is rejected. TV programs have different preferences for different age groups.

Practice 11.2.2 To evaluate the effectiveness of typing training, 100 documents by company employees who received type training and 100 documents by employees who did not receive typing training were evaluated. Evaluated documents are classified as good, normal, and low. The following table shows a classification of the evaluation for total 200 documents according to whether or not they received training. Test the null hypothesis that distributions of the document evaluation are the same In both populations. Use \(\alpha\) = 0.05 and check your test result using 『eStatU』.

Evaluation \ Training Typing training No training Total
Good 48 12 60
Normal 39 26 65
Low 13 62 75
Total 100 100 200

11.3 Exercise