Since a population is generally very large, a survey of the entire population takes lots of time and money. Hence we are trying to estimate characteristics of the population using a set of samples. Estimation of population characteristics using samples is called an inferential statistics. However, there may be some difference between the characteristic of the population and the characteristic of the sample. In order to reduce the difference, several methods of sampling have been studied. The most commonly used one is a simple random sampling which collects samples with the same probability of all elements of the population being selected.
Chapter 6. Sampling Distribution and Estimation
[book] [eStat YouTube Channel]
- 6.1 Simple Random Sampling
- 6.2 Sampling Distribution of Sample Means and Estimation of the Population Mean
- 6.3 Sampling Distribution of Sample Variances and Estimation of the Population Variance
- 6.4 Sampling Distribution of Sample Proportions and Estimation of the Population Proportion
- 6.5 Determination of the Sample Size
- 6.6 Application of Sampling Distribution: Quality Control Chart
- 6.7 Exercise
CHAPTER OBJECTIVES
The power of modern statistics lies in the ability to predict the characteristics of a population with a small number of samples. The sampling methods ares introduced to collect a sample from the population in Section 6.1.Section 6.2 describes the distribution of all possible sample means and its application to estimate the population mean.
Section 6.3 describes the distribution of all possible sample variances and its application to estimate the population variance.
Section 6.4 describes the distribution of all possible sample proportions and its application to estimate the population proportion.
Section 6.5 describes how to determine the sample size to estimate the population mean and population proportion.
Section 6.6 describes an application of sampling distribution to the quality control chart for a production process.
6.1 Simple Random Sampling
[presentation] [video]
Samples are collected so that all elements of the population are likely to be selected equally.
Some tools may be needed to ensure that each element of the population is selected equally. We usually use a random number table which is a table of numbers from 0 to 9 without special regularity or partiality. Recently, a random number generator by using a computer which uses the uniform distribution on [0, 1] is widely used to produce a random number. 『eStatU』 provide random number generators for Uniform, Normal and two dimensional Normal distributions.
Answer
In order to select three samples randomly from 50 students, a list of students which assigned serial numbers from one to fifty must be made first. In order to collect samples, select [Random Number Generator] in 『eStatU』 menu. Enter (1 and 50) at the box of ‘Uniform’, ‘Integer (without replacement)’, enter 3 at the box of ‘Number of Data’ and click the [Execute] button as shown in <Figure 6.1.1>. These are the random numbers to select students, but your computer might generate different numbers, because it depends on computer.
[Random Number Generation]
If you read the three numbers from located above, you will choose these student numbers as samples.
Generated random numbers may have same numbers. If it is a sampling without replacement, discard the following same number.
6.1.1 Sample Survey
Each element of the population that is the subject of analysis is called an elementary unit or an observational unit because it is the object that is actually observed in the survey. Depending on the sampling method, these elementary units can be selected individually (e.g. simple random sampling method), or a set of elementary units can be selected for convenience of sampling. Therefore, what is selected to construct a sample is called a sampling unit, distinguishing it from an observational unit. In order to select samples by the sampling unit, a table of the sampling units is required, which is called a sampling frame. Describing how to select samples using the sampling frame is called a sampling design.
In order to conduct a good sample survey, it is necessary to define accurately the above terms in advance. Since a sample survey is a method of scientific research, all steps for a sample survey must be planned in advance and carried out according to the plan.
Steps for Sample Survey
Stratified Sampling
Cluster Sampling
System Sampling
6.2 Sampling Distribution of Sample Means and Estimation of the Population Mean
[presentation] [video]
[Population vs Sample]
6.2.1 Sampling Distribution of Sample Means
Answer
| Sample | Sample Mean \(\small \overline X \) |
|---|---|
| 2, 2 | 2 |
| 2, 4 | 3 |
| 2, 6 | 4 |
| 2, 8 | 5 |
| 2,10 | 6 |
| 4, 2 | 3 |
| 4, 4 | 4 |
| 4, 6 | 5 |
| 4, 8 | 6 |
| 4,10 | 7 |
| 6, 2 | 4 |
| 6, 4 | 5 |
| 6, 6 | 6 |
| 6, 8 | 7 |
| 6,10 | 8 |
| 8, 2 | 5 |
| 8, 4 | 6 |
| 8, 6 | 7 |
| 8, 8 | 8 |
| 8,10 | 9 |
| 10,2 | 6 |
| 10,4 | 7 |
| 10,6 | 8 |
| 10,8 | 9 |
| 10,10 | 10 |
\( \qquad \small \mu_{\overline X} = \frac { 2 + 3×2 + 4×3 + 5×4 + 6×5 + 7×4 + 8×3 + 9×2 + 10} { 25} = 6 \)
\( \qquad \small \sigma_{\overline X}^2 = \frac {(2-6)^{2} +(3-6)^{2} \times 2 + (4-6)^{2} \times 3 + (5-6)^{2} \times 4 + (6-6)^{2} \times 5 + (7-6)^{2} \times 4 + (8-6)^{2} \times 3 + (9-6)^{2} \times 2 + (10-6)^{2}} {25} = 4 \)
| Sample Mean | Frequency | Relative Frequency |
|---|---|---|
| 2 | 1 | 0.04 |
| 3 | 2 | 0.08 |
| 4 | 3 | 0.12 |
| 5 | 4 | 0.16 |
| 6 | 5 | 0.20 |
| 7 | 4 | 0.16 |
| 8 | 3 | 0.12 |
| 9 | 2 | 0.08 |
| 10 | 1 | 0.04 |
| 25 | 1.00 |
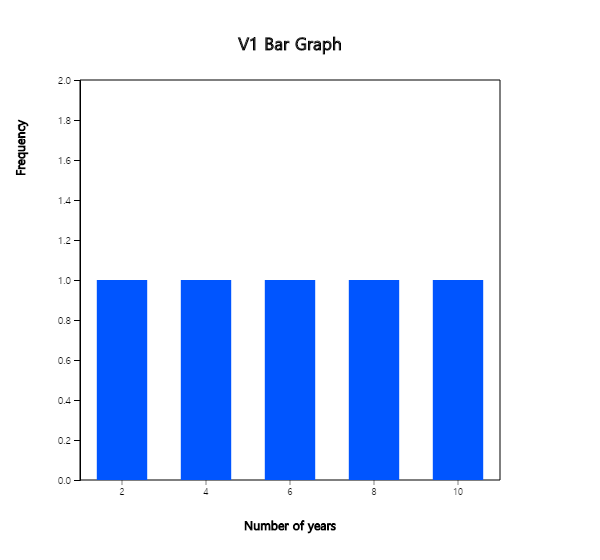
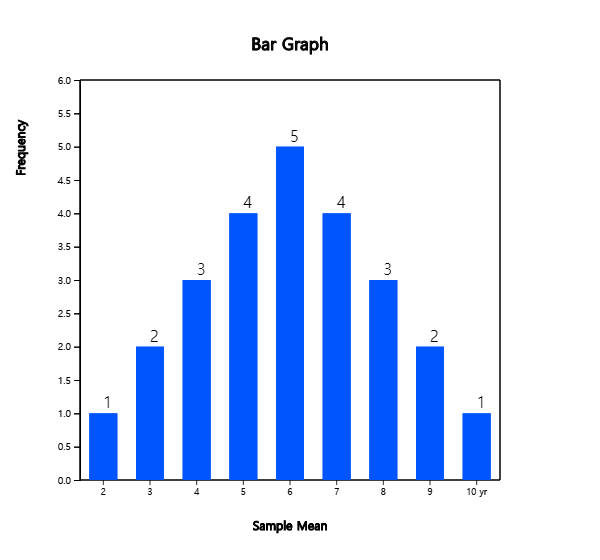
The population mean is a single value, but there are many possible sample means. The population mean μ is called a parameter, which is a characteristic value of the population, and the sample mean is a random variable that can have many different values and is usually expressed with a capital letter such as \(\small \overline X \) which is called an estimator of the parameter μ. An observed sample mean, marked \(\small \overline x \) with a lowercase letter, is called an estimate of μ.
An estimator of the population variance \( σ^2 \) is the sample variance \( S^2 \) and its observed value which is an estimate of \( S^2 \) is denoted as \( s^2 \).
The relationship between the population mean and all possible sample means in [Example 6.2.1] is observed even if the population has a different shape of distribution. If the population is very large, it is not possible to find all possible samples as shown in [Example 6.2.1] and to find a distribution of sample means. Therefore, the following theoretical research has been developed.
If a population is normally distributed with \( N(μ, σ^2 ) \), the distribution of all possible sample means is exactly a normal distribution such as \( N(μ, \frac {σ^2 }{n} ) \). If the population is an infinite population with the mean μ and variance \( σ^2 \), then the distribution of all possible sample means is approximately a normal distribution such as \( N(μ, \frac {σ^2 }{n} ) \) if the sample size is large enough. This is referred to as the Central Limit Theorem, which is a key theory in statistics, specifically summarized as follows.
Suppose a population is not a normal distribution and its mean and variance are μ and \( σ^2 \). If we select samples of size with replacement, the distribution of all possible sample means has following characteristics:
The above facts can be briefly written as \(\small \overline {X} \sim N(μ, \frac {σ^2}{n} ) \).
[Sampling Distribution of Sample Means]
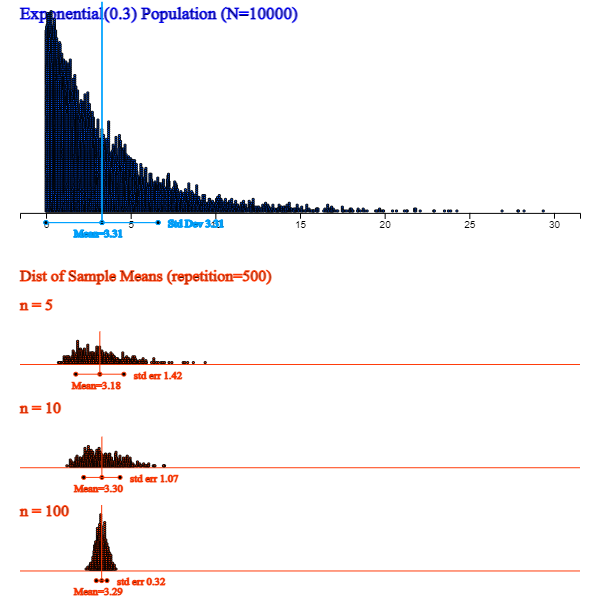
<Figure 6.2.5> shows a simulation using 『eStatU』 that, although a population is skewed from its mean, the distribution of sample means is closer to normal as the sample size increases.
6.2.2 Estimation of the Population Mean
[presentation] [video]
This is a basic question on the estimation that everyone can think about at least once. The sampling distribution of all possible sample means which we studied in the previous section is the answer to this question. That is, whatever a population distribution is, if the sample size is large enough, all possible sample means are clustered around the population mean in the form of a normal distribution. Therefore, the sample mean obtained from one set of samples is usually close to the population mean. Even in the worst case, the difference between the population mean and sample mean, known as an error, is not so significant, and it is possible to estimate the population mean by using the sample mean. The larger the sample size, the more sample means are concentrated around the population mean based on the central limit theorem and hence we can reduce the error of the estimation.
Point Estimation of the Population Mean
In general, the sample statistic used to estimate a population parameter must have good characteristics, so that the estimate can be accurate. If the average of all possible sample statistics is equal to the population parameter, then the sample statistic has a good chance to estimate the population parameter and it is called an unbiased estimator. In the previous section we found that a sample mean is an unbiased estimator of the population mean.
If the value of a sample statistic becomes closer and closer to the population parameter when the sample size grows, the sample statistic is called a consistent estimator. The variance of all possible sample means is closer to zero as the sample size increases by the central limit theorem studied in the previous section, so the sample mean is closer to the population mean. Therefore, the sample mean is a consistent estimator of the population mean.
If a sample statistic has the least variance when there are several unbiased estimators for the population parameter, it is called an efficient estimator. The sample mean is also an efficient estimator. Consequently, a sample mean has all good characteristics necessary to estimate the population mean.
A value of one observed sample mean is called a point estimate of the population mean.
If the average value of all possible sample statistics is equal to the population parameter, then the sample statistic is called an unbiased estimator of the population parameter. The sample mean is an unbiased estimator of the population mean.
When a sample size grows, if the value of the sample statistic becomes closer and closer to the population parameter, the sample statistic is called a consistent estimator. The sample mean is a consistent estimator of the population mean.
If a sample statistic has the least variance when there are several unbiased estimators for the population parameter, it is called an efficient estimator. The sample mean is an efficient estimator.
(Note that \(\small \overline X \) is an unbiased, consistent, efficient estimator of μ).
Interval Estimation of the Population Mean – Known Population Variance
In contrast to the point estimate for the population mean, estimating population mean by using an interval is called an interval estimation. If the population is a normal distribution with the mean μ and variance \(σ^2 \), the distribution of all possible sample means is a normal distribution with the mean μ and variance \(\frac {σ^2}{n} \), so the probability that one sample mean will be included in the interval \( μ ± 1.96 \times \frac {σ}{\sqrt{n}} \) is 95% as follows. $$\small P(\mu - 1.96 \times \frac {σ}{\sqrt{n}} < \overline X < \mu + 1.96 \times \frac {σ}{\sqrt{n}} ) = 0.95 $$ We can rewrite this formula as follows. $$\small P(\overline X - 1.96 \times \frac {σ}{\sqrt{n}} < \mu < \overline X + 1.96 \times \frac {σ}{\sqrt{n}} ) = 0.95 $$ Assuming σ is known, the meaning of the above formula is that 95% of intervals obtained by applying the formula \(\small [ \overline {X} - 1.96 \times \frac {σ}{\sqrt{n}}, \overline {X} + 1.96 \times \frac {σ}{\sqrt{n}} ] \) for all possible sample means include the population mean. The formula of this interval is referred to as the 95% confidence interval of the population mean. $$\small \left[ \overline {X} - 1.96 \times \frac {σ}{\sqrt{n}}, \overline {X} + 1.96 \times \frac {σ}{\sqrt{n}} \right] $$
Generally, since \(\small \overline {X} \sim N(μ, \frac {σ^2}{n} ) \), the standardized random variable of \(\small \overline X \), \(\small Z = \frac {\overline X - \mu}{\frac {\sigma}{\sqrt n}} \), follows the standard normal distribution \(N(0,1)\). Therefore, the following probability of the standard normal random variable \(Z\) is \(1-α\) . $$\small P \left( -z_{\alpha/2} < \frac {\overline{X} - \mu } {\sigma/\sqrt{n}} < z_{\alpha/2} \right) = P ( -z_{\alpha/2} < Z < z_{\alpha/2} ) = 1 - \alpha $$ This formula can be written as follows: $$\small P \left( \mu - z_{\alpha/2} \frac {\sigma} {\sqrt{n}} < \overline X < \mu + z_{\alpha/2} \frac {\sigma} {\sqrt{n}} \right) = 1 - \alpha $$ This formula can also be written as follows: $$\small P \left( \overline X - z_{\alpha/2} \frac {\sigma} {\sqrt{n}} < \mu < \overline X + z_{\alpha/2} \frac {\sigma} {\sqrt{n}} \right) = 1 - \alpha $$ The confidence interval for the population mean μ is as follows if the population is normally distributed and the population variance \( \sigma^2 \) is known.
Assume a population is a normal distribution and the population variance is known. $$\small \left[ \overline X - z_{\alpha/2} \frac {\sigma} {\sqrt{n}} , \overline X + z_{\alpha/2} \frac {\sigma} {\sqrt{n}} \right] $$
100(1-α)% here is called a confidence level, which refers to the probability of intervals that will include the population mean among all possible intervals calculated by the confidence interval formula. Usually, we use 0.01 or 0.05 for α. \( z_{α} \) is the upper α percentile of the standard normal distribution. In other words, if \(Z\) is the random variable which follows the standard normal distribution, the probability that \(Z\) is greater than \( z_{α} \) is α, i.e., $$ P(Z > z_{α} ) = α $$ For example, \( z_{0.025;} \) = 1.96, \( z_{0.95} \) = -1.645, \( z_{0.005} \) = 2.575.
<Figure 6.2.6> shows a simulation of the 95% confidence interval for the population mean by extracting 100 sets of samples with the sample size \(n\) = 20 from a population of 10,000 numbers which follow the standard normal distribution N(0,1). In this case, 96 of the 100 confidence intervals contain the population mean 0. This result might be different on your computer, because the program use a random number generator which depends on computer. Whenever we repeat these experiments, the result may also vary slightly.
[Confidence Interval Experiment]
Answer
\( \qquad \small z_{α/2} = z_{0.05/2} = 1.96 \)
\( \qquad \small \left[ \overline X - z_{\alpha/2} \frac {\sigma} {\sqrt{n}} , \overline X + z_{\alpha/2} \frac {\sigma} {\sqrt{n}} \right] \)
\( \qquad \small ⇔ [ 275 - 1.96 \frac{5}{10}, 275 + 1.96 \frac{5}{10} ] \)
\( \qquad \small ⇔ [274.02, 275.98] \)
\( \qquad \small z_{α/2} = z_{0.01/2} = 2.575 \)
\( \qquad \small ⇔ [ 275 - 2.575 \frac{5}{10}, 275 + 2.575 \frac{5}{10} ] \)
\( \qquad \small ⇔ [273.71, 276.29] \)
\( \qquad \small ⇔ [ 275 - 1.96 \frac{5}{20}, 275 + 1.96 \frac{5}{20} ] \)
\( \qquad \small ⇔ [274.51, 275.49] \)
Interval Estimation of the Population Mean – Unknown Population Variance
One problem in estimating the unknown population mean by using the formula of the confidence interval in the previous section is that either the population variance may not be known or the population is not normally distributed. If the sample size is large enough, a confidence interval of the population mean can be obtained approximately using the sample variance instead of the population variance on the previous formula. However, if the sample size is small and the sample variance is used, a confidence interval based on the t distribution should be used.
The \(t\) distribution was studied by a statistician W. S. Gosset, who worked for a brewer in Ireland, and published his study result in 1907 under the alias Student. So \(t\) distribution is often referred to as Student's \(t\) distribution. The \(t\) distribution is not just a single distribution, but it is a family of distributions under a parameter called a degree of freedom, 1,2, ... , 30, ... and denoted as \(t_1 ,t_2 , ... , t_{30} , ... \)
The shape of the \(t\) distribution is symmetrical about zero (y axis), similar to the standard normal distribution, but it has a tail that is flat and longer than the standard normal distribution. <Figure 6.2.7> shows the standard normal distribution N(0,1) and \(t\) distribution with 3 degrees of freedom at the same time by using the \(t\) distribution module of 『eStatU』.
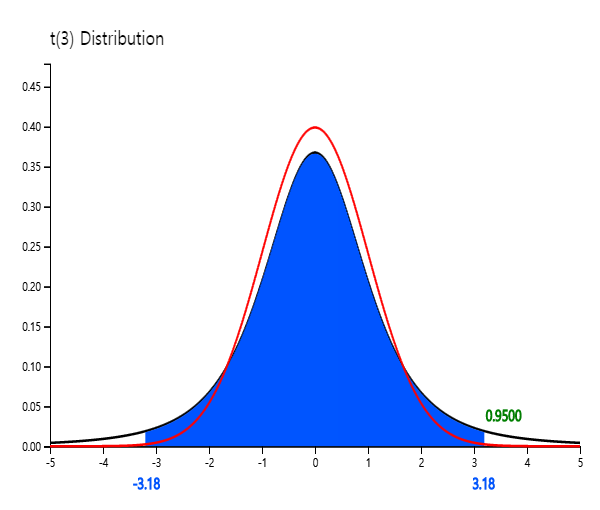
The \(t\) distribution is closer to the standard normal distribution as degrees of freedom increase above 30. This is why a confidence interval can be obtained approximately by using the standard normal distribution if the sample size is greater than 30. Denote \(t_{n:α}\) as the 100(1-α)% percentile of the \(t\) distribution with \(n\) degrees of freedom. For example, \(t_{7:0.05}\) is the 100(1-0.05)=95% percentile of the \(t\) distribution and its value is 1.895 as <Figure 6.2.8>. In the standard normal distribution, this value was 1.645. Since the \(t\) distribution is symmetrical, \(t_{n:α} = -t_{n:1-α}\).
In order to find a percentile value of the \(t_{7}\) distribution using 『eStatU』, click on '\(t\) distribution' in the main menu of 『eStatU』 and then set the degree of freedom (df) to 7, and set the probability value in the fifth option below the \(t\) distribution graph to 0.95, then \(t_{7:0.05}\) = 1.895 will appear as in <Figure 6.2.8>.
[t Distribution]
Consider the interval estimation of the population mean when you do not know the population variance, but assume that the population is a normal distribution. If \( X_1 , X_2 , ... , X_n \) is the random sample of size \(n\) from the normal population, then it can be shown that the distribution of \( \frac {\overline X -\mu}{S/\sqrt{n}} \), where σ is replaced with S, is the \(t\) distribution with \( n-1 \) degrees of freedom. $$\small \frac {\overline X -\mu}{\frac{S}{\sqrt{n}}} \sim t_{n-1} $$ Hence the probability of the (1 - α)% interval is as follows. $$\small P \left( -t_{n-1;\alpha/2} < \frac {\overline{X} - \mu } {S\sqrt{n}} < t_{n-1:\alpha/2} \right) = 1 - \alpha $$ The left hand side of the above formula can be summarized as the confidence interval for the population mean when the population variance is unknown as follows:
Assume a population is a normal distribution and the population variance \(σ^2\) is unknown. $$\small \left[ \overline X - t_{n-1:\alpha/2} \frac {S} {\sqrt{n}} , \overline X + t_{n-1:\alpha/2} \frac {S} {\sqrt{n}} \right] $$
where \(n\) is the sample size and \(S\) is the sample standard deviation.
Answer
Since we do not know the population variance, \(t\) distribution should be used for interval estimation of the population mean.
Since \( t_{n-1:\alpha/2} = t_{25-1:0.05/2} = t_{25-1:0.025} = 2.0639 \), the 95% confidence interval of the population mean is as follows. $$ \small \begin{multline} \shoveleft \left[ \overline X - t_{n-1:\alpha/2} \frac {S} {\sqrt{n}} , \overline X + t_{n-1:\alpha/2} \frac {S} {\sqrt{n}} \right] \\ \shoveleft ⇔ [ 275 - 2.0639(5/5) , 275 + 2.0639(5/5) ] \\ \shoveleft ⇔ [ 272.9361, 277.0639 ] \end{multline} $$ Note that the smaller the sample size, the wider the interval width.
171 172 185 169 175 177 174 179 168 173
Answer
Click [Estimation : μ Confidence Interval] on the menu of 『eStatU』 and enter data at the [Sample Data] box as <Figure 6.2.9>. Then the confidence intervals [170.68, 177.92] are calculated using the \(t_9\) distribution.
In this 『eStatU』 module, confidence intervals can be obtained by entering the sample sizes, sample mean, and sample variance without entering data.
[ ]
In this module of 『eStatU』, a simulation experiment to investigate the size of the confidence interval can be done by changing the sample size \(n\) and the confidence level 1 - α as in <Figure 6.2.10>. If you increase \(n\), the interval size becomes narrower. If you increase 1 - α, the interval size becomes wider.
6.3 Sampling Distribution of Sample Variances and Estimation of the Population Variance
[presentation] [video]
If we know the relationship between the population variance and the sample variance, it is possible to estimate the population variance. In this section, the distribution of all possible sample variances is discussed in section 6.3.1 and the estimation of the population variance using the sample variance is discussed in section 6.3.2.
6.3.1 Sampling Distribution of Sample Variances
6, 2, 4, 8, 10
Answer
| Sample | Sample Variance \( s^2\) |
|---|---|
| 2, 2 | 0 |
| 2, 4 | 2 |
| 2, 6 | 8 |
| 2, 8 | 18 |
| 2,10 | 32 |
| 4, 2 | 2 |
| 4, 4 | 0 |
| 4, 6 | 2 |
| 4, 8 | 8 |
| 4,10 | 18 |
| 6, 2 | 8 |
| 6, 4 | 2 |
| 6, 6 | 0 |
| 6, 8 | 2 |
| 6,10 | 8 |
| 8, 2 | 18 |
| 8, 4 | 8 |
| 8, 6 | 2 |
| 8, 8 | 0 |
| 8,10 | 2 |
| 10,2 | 32 |
| 10,4 | 18 |
| 10,6 | 8 |
| 10,8 | 2 |
| 10,10 | 0 |
\( \qquad \small \mu_{s^2} = \frac {0 \times 5 + 2 \times 8 + 8 \times 6 + 18 \times 4 + 32 \times 2} {25} = 8 \)
Note that the average of all possible sample variances is the same as the population variance which means the sample variance is an unbiased estimate of the population variance.
| Sample Variance | Frequency | Relative Frequency |
|---|---|---|
| 0 | 5 | 0.20 |
| 2 | 8 | 0.32 |
| 8 | 6 | 0.24 |
| 18 | 4 | 0.16 |
| 32 | 2 | 0.08 |
| total | 25 | 1.00 |
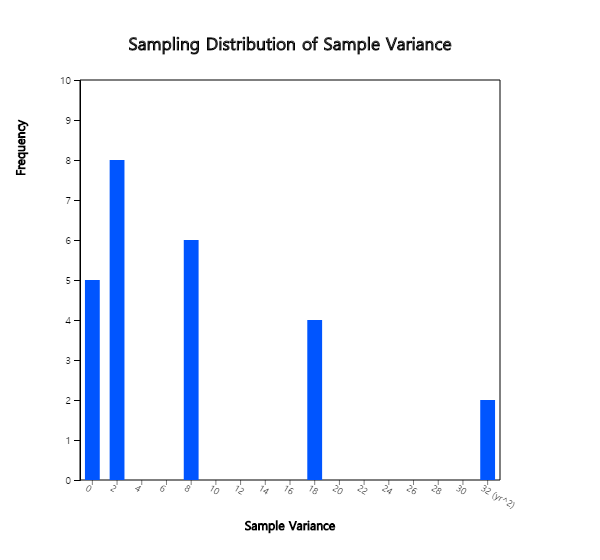
As observed in the above example, the sampling distribution of the sample variances is an asymmetric distribution with many small sample variances and a few large sample variances. In general, when the population is normally distributed and the population variance is \(σ^2\), all possible sample variances scaled by a constant follow the chi-square \(χ^2\) distribution. More accurately, the sample statistic $$ \frac {(n-1)S^2}{\sigma^2} $$ follows a chi-square distribution with \(n-1\) degrees of freedom.
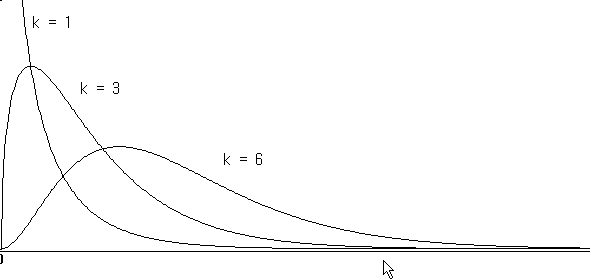
This chi-square distribution is a family of distributions depending on the degree of freedom, such as \(χ^2_{1} , χ^2_{2} , ... , χ^2_{27} , ...\) etc. The chi-square distribution is an asymmetrical distribution as <Figure 6.3.2>. If the degree of freedom is small, the shape of the chi-square distribution is much skewed to the right.
A cumulated probability and a percentile of the chi-square distribution can be calculated by using 『eStatU』 as in <Figure 6.3.3>.
[ ]
The sampling distribution of all sample variances is summarized as follows:
When the population is normally distributed and the sample of size \(n\) is selected randomly with replacement, the distribution of all sample variances multiplied by a specific constant follows the chi-square distribution with \(n-1\) degrees of freedom as follows. $$ \frac {(n-1)S^2}{\sigma^2} \sim \chi^2_{n-1} $$
6.3.2 Estimation of the Population Variance
[presentation] [video]
Examples of estimating the population variance are as follows.
In order to estimate the population variance, the sampling distribution of all possible sample variances should be used. As discussed in [Example 6.3.1], for an infinite population, the mean of all possible sample variances is the population variance. That is, the sample variance \(S^2\) is an unbiased estimator of the population variance \(σ^2\). Therefore, the sample variance is used to estimate the population variance. In addition, estimation of the population standard deviation \(σ\) uses the sample standard deviation \(S\), but it should be noted that the sample standard deviation is not an unbiased estimator of the population standard deviation. However, as the sample size increases, there is no significant error in using \(S\) as an estimator of \(σ\).
⇒ Sample variance \(S^2\) (\(S^2\) is an unbiased estimator of \(σ^2\))
Point estimation of the population standard deviation \(σ\)
⇒ Sample standard deviation \(s\) (\(s\) is not an unbiased estimator of \(σ\))
Assume that a population is normally distributed. $$ \left[ \frac {(n-1)S^2}{\chi^2_{n-1: α/2} }, \frac {(n-1)S^2}{\chi^2_{n-1: 1-α/2} } \right] $$ where \(S^2\) is the sample variance, \(χ^2_{k:p}\) is the 100\((1-p)\) percentile of the chi-square distribution with \(k\) degrees of freedom.
100(1-α)% Confidence interval of the population standard deviation \(σ\)
Assume a population is normally distributed and the sample size is large. $$ \left[ \sqrt { \frac {(n-1)S^2}{\chi^2_{n-1: α/2} } }, \sqrt { \frac {(n-1)S^2}{\chi^2_{n-1: 1-α/2} } }\right] $$
Answer
The point estimate of the population variance for the starting salary of college graduate is the sample variance, so \(s^2 = 5^2 =\) 25. Since the point estimate of the population standard deviation is the sample standard deviation, so \(s =\) 5.
The 95% confidence interval of the population variance is as follows. $$ \small \begin{multline} \shoveleft \left[ \frac {(n-1)S^2}{\chi^2_{25-1: 0.05/2} }, \frac {(n-1)S^2}{\chi^2_{25-1: 1-0.05/2} } \right] \\ \shoveleft ⇒ \left[ \frac {(25-1)5^2}{39.364}, \frac {(25-1)5^2}{12.401} \right] \\ \shoveleft ⇒ \left[ 15.242, 48.383 \right] \end{multline} $$ The 95% confidence interval of the population standard deviation is as follows. $$ \small \begin{multline} \shoveleft ⇒ \left[ \sqrt{15.242}, \sqrt{48.383} \right] \\ \shoveleft ⇒ \left[ 3.904, 6.956 \right] \end{multline} $$
171 172 185 169 175 177 174 179 168 173
Using 『eStatU』, find a 95% confidence interval for estimating the population variance of college freshmen.
Answer
On the menu of 『eStatU』, click [Estimation : \(σ^2\) Confidence Interval] and enter data in the [Sample Data] box as shown in <Figure 6.3.4>. The system will show the confidence interval [12.10, 85.21] immediately by using the chi-square distribution.
[ ]
In this module of 『eStatU』, a simulation experiment to investigate the size of the confidence interval can be done by changing the sample size \(n\) and the confidence level 1 - α as in <Figure 6.3.5>. If you increase \(n\), the interval size becomes narrower. If you increase 1 - α, the interval size becomes wider.
You can enter only the sample size and sample variance to calculate the confidence interval in this 『eStatU』 module without entering data.
2.87 2.05 2.90 2.41 2.93 2.94 2.26 2.21 2.20 2.88
Use 『eStatU』 to find a 95% confidence interval of the population variance of oxygen consumed.
6.4 Sampling Distribution of Sample Proportions and Estimation of the Population Proportion
[presentation] [video]
If we know the relationship between the population proportion and sample proportion, it is possible to estimate the population proportion. In this section, the distribution of all possible sample proportions is discussed in section 6.4.1 and the estimation of the population proportion using the sample proportion is discussed in section 6.4.2.
6.4.1 Sampling Distribution of Sample Proportions
Consider the sampling distribution of all possible sample proportions by using the following example.
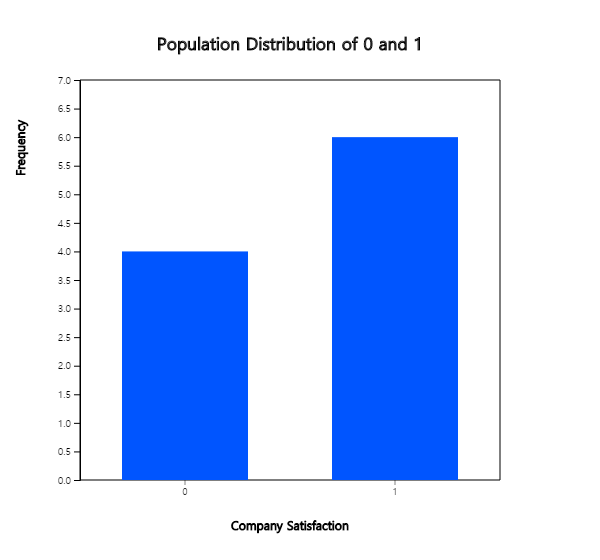
1 0 1 1 0 1 1 0 0 1
That is, the population proportion \(p\) of the satisfaction is 0.6 (6 ‘1’s out of 10). Consider all possible samples of size 5 with replacement to obtain a sampling distribution of sample proportions. (It is to illustrate the sample variance of sample proportions, although it is not necessary to extract samples from such a small population.)
Answer
The population proportion is \(p\) = 0.6 and the distribution of ‘1’ and ‘0’ in the population consisting of 10 persons is as <Figure 6.4.1>.
Total number of possible samples of size 5 with replacement is 10×10×10×10×10 = 100000 and the number of cases of possible sample proportions are as in Table 6.4.1.
| Sample Case | Number of Cases |
|---|---|
| all unsatisfactory (0,0,0,0,0) | \(\small {}_{5}C_{0}\)×4×4×4×4×4 = 1024 |
| 1 satisfactory (0,0,0,0,1) | \(\small {}_{5}C_{1}\)×4×4×4×4×6 = 7680 |
| 2 satisfactory (0,0,0,1,1) | \(\small {}_{5}C_{2}\)×4×4×4×6×6 = 23040 |
| 3 satisfactory (0,0,1,1,1) | \(\small {}_{5}C_{3}\)×4×4×6×6×6 = 34560 |
| 4 satisfactory (0,1,1,1,1) | \(\small {}_{5}C_{4}\)×4×6×6×6×6 = 25920 |
| 5 satisfactory (1,1,1,1,1) | \(\small {}_{5}C_{5}\)×6×6×6×6×6 = 7776 |
| Total | 100000 |
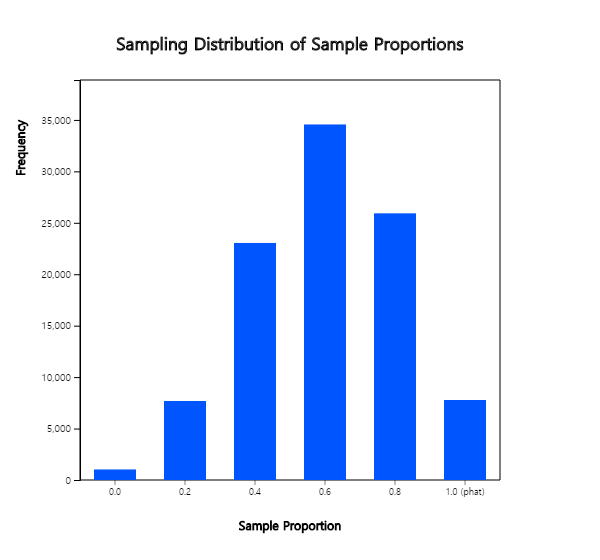
If the sample proportion (\(\hat p\)) is obtained from each case, the sampling distribution of all possible sample proportions is as Table 6.4.2. The cases of three satisfactory (the sample proportion of 0.6) are most likely.
| Sample Case | Sample Proportion \(\hat p\) | Frequency | Relative Frequency |
|---|---|---|---|
| all unsatisfactory (0,0,0,0,0) | 0.0 | 1024 | 0.01024 |
| 1 satisfactory (0,0,0,0,1) | 0.2 | 7680 | 0.07680 |
| 2 satisfactory (0,0,0,1,1) | 0.4 | 23040 | 0.23040 |
| 3 satisfactory (0,0,1,1,1) | 0.6 | 34560 | 0.34560 |
| 4 satisfactory (0,1,1,1,1) | 0.8 | 25920 | 0.25920 |
| 5 satisfactory (1,1,1,1,1) | 1.0 | 7776 | 0.07776 |
| Total | 100000 | 1.00000 |
<Figure 6.4.2> shows the sampling distribution of all possible sample proportions. If the sample size is larger, sample proportions are symmetrical around the population proportion 0.6 which is similar to that of sample means, and is close to a normal distribution.
Assume the population is infinite and the population proportion is \(p\). If \(\hat p\) is the sample proportion and the sample size \(n\) is large, the sampling distribution of all possible sample proportions is approximately a normal distribution with the mean \(p\) and variance \(\frac {p(1-p)}{n}\) . $$ \hat p \sim N \left( p, \frac{p(1-p)}{n} \right) $$
Answer
Since the sampling distribution of the sample proportions is approximately normal distribution, \(\hat p \sim N \left( p, \frac{p(1-p)}{n} \right) \), the probability can be calculated as follows:
\( \quad \small P(\hat p \gt 0.02) = P( Z \gt \frac{0.02-0.03}{0.00985} ) = P(Z \gt -1.02) = 1 - P(Z \le -1.02) = 1 - 0.1539 = 0.8461 \)
6.4.2 Estimation of the Population Proportion
[presentation] [video]
Some practical examples to estimate the population proportion are as follows.
Assume that the proportion of a population is \(p\). As discussed in Section 6.1, since the sample proportion, \(\hat p\), meets all the criteria of a good estimator when estimating the population proportion \(p\), the sample proportion is used to estimate the population proportion. The sampling distribution of all possible sample proportions is approximately a normal distribution with the mean \(p\) and variance \(\frac{p(1-p)}{n}\) and the standard error of the sample proportions is \(\sqrt{\frac{p(1-p)}{n}}\). But, since the population proportion \(p\) is unknown, we use \(\sqrt{\frac{\hat p(1- \hat p)}{n}}\) as an estimate of the standard error of the sample proportions.
⇒ The sample proportion \(\hat p\).
The sample proportion (\(\hat p\)) is an unbiased, efficient and consistent estimator of the population proportion \(p\) and the estimate of the standard error of \(\hat p\) is \(\sqrt{\frac{\hat p(1- \hat p)}{n}}\).
If the population proportion is \(p\), 100(1-α)% confidence interval of \(p\) when the sample size \(n\) is large is as follows. $$ \left[ \hat p - z_{α/2} \sqrt{\frac{\hat p (1-\hat p)}{n} }, \hat p + z_{α/2} \sqrt{\frac{\hat p (1-\hat p)}{n} } \right] $$
Criteria of large sample size \(n\) are \( n \hat p > 5 , n (1- \hat p ) > 5 \).
Answer
The point estimate of the population approval rating is the sample proportion.
\( \qquad \quad \small \hat p = \frac {120}{200} = 0.6 \)
The 95% confidence interval is as follows: $$ \small \begin{multline} \shoveleft \left[ \hat p - z_{α/2} \sqrt{\frac{\hat p (1-\hat p)}{n} }, \hat p + z_{α/2} \sqrt{\frac{\hat p (1-\hat p)}{n} } \right] \\ \shoveleft ⇔ \left[ 0.6 - 1.96 \sqrt{\frac{0.6(1-0.6)}{200} }, 0.6 + 1.96 \sqrt{\frac{0.6(1-0.6)}{200} } \right] \\ \shoveleft ⇔ \left[ 0.532 , 0.668 \right] \end{multline} $$ In 『eStatU』, enter data in the [Sample Data] box as shown in <Figure 6.4.3> and click the [Execute] button to calculate the confidence interval [0.5321, 0.6679] using the normal distribution.
[ ]
In this module of 『eStatU』, a simulation experiment to investigate the size of the confidence interval can be done by changing the sample size \(n\) and the confidence level 1 - α as in <Figure 6.4.4>. If you increase \(n\), the interval size becomes narrower. If you increase 1 - α, the interval size becomes wider.
6.5 Determination of the Sample Size
[presentation] [video]
6.5.1 Determination of the Sample Size to Estimate the Population Mean
If the maximum allowable error bound and the confidence level 1-α are given, the sample size can be determined by solving the following equation. $$ z_{\alpha/2} \frac {\sigma} {\sqrt{n}} = d $$ The solution of \(n\) in the above equation is as follows. $$ n = {\left( \frac { z_{\alpha/2} {\sigma} } {d} \right)}^2 $$
If the maximum allowable error bound \(d\) and the confidence level 1-\(\alpha\) are given, the sample size \(n\) can be determined as follows: $$ n = {\left( \frac { z_{\alpha/2} {\sigma} } {d} \right)}^2 $$
Answer
\( \qquad \small n = {\left( \frac { z_{\alpha/2} {\sigma} } {d} \right)}^2 = {\left( \frac { 1.96 \times 100} {20} \right)}^2 = 9.8^2 = 96.04 \)
Hence the sample size is 96 approximately.
In 『eStatU』, select the menu [Estimation : μ - Sample Size]. Enter the margin of Error \(d\) = 20, the population standard deviation σ = 100 and confidence level 1-α = 0.95 as in <Figure 6.5.1>, then click the [Execute] button to calculate the sample size \(n\).
[ - n]
6.5.2 Determination of the Sample Size to Estimate the Population Proportion
As explained in section 6.4, the 100(1-α)% confidence interval of a population proportion \(p\) is as follows. $$ \left[ \hat p - z_{α/2} \sqrt{\frac{\hat p (1-\hat p)}{n} }, \hat p + z_{α/2} \sqrt{\frac{\hat p (1-\hat p)}{n} } \right] $$
The term \(z_{α/2} \sqrt{\frac{\hat p (1-\hat p)}{n} }\) which is the half size of the confidence interval is called the maximum allowable error bound to estimate the population proportion and is denoted as \(d\).
Therefore, if the maximum allowable error bound \(d\) and the confidence level 1-α are given, the sample size can be determined by solving the following equation. $$ z_{α/2} \sqrt{\frac{\hat p (1-\hat p)}{n} } = d $$ The solution of the above equation is as follows. $$ n = \hat p (1-\hat p) ( {\frac{z_{α/2}}{d}} )^2 $$
If the maximum allowable error bound \(d\) and the confidence level 1 - α are given, the sample size can be determined as follows: $$ n = \hat p (1-\hat p) ( {\frac{z_{α/2}}{d}} )^2 $$
Answer
Since we do not have any information on the population proportion, assume \(\hat p\) = 0.5. Then the sample size can be calculated as follows:
\( \qquad \small n = \hat p (1-\hat p) ( {\frac{z_{α/2}}{d}})^2 = 0.5(1-0.5)\frac{1.96^2}{0.025^2} = 1536.6 \)
Therefore, samples must be extracted with at least 1537 persons to limit the error bound to 2.5%. Various opinion polls conducted nationwide often show that the size of the sample is around 1,500 which implies that the margin of error does not exceed 3 percent.
In 『eStatU』, select the menu [Estimation : \(p\) - Sample Size \(n\)]. Enter the margin of Error \(d\) = 0.025, the estimate of the sample proportion \(\hat p\) = 0.5 (since we don’t know \(\hat p\), it is an estimate), and the confidence level 1 - α = 0.95 as in <Figure 6.5.2>, then click the [Execute] button to calculate the sample size .
[ - n]
6.6 Application of Sampling Distribution: Quality Control Chart
[presentation]
A control chart is a diagram to manage changes in quality characteristic values. As shown in <Figure 6.6.1>, there is an upper control limit (UCL) at the top, a center line (CL) in between, and a lower control limit (LCL) at the bottom. The characteristic value of an inspected sample in each time are plotted as a line graph. When the quality characteristic values do not exceed the control limit lines and are not related to each other, the process is said to be under control. If the quality characteristic value is outside the control limits or, if the characteristic values are related each other even they are within the control limits, the process is said to be out of control.
Control charts are divided into a control chart by variable and control chart by attribute.
6.6.1 Control Charts by Variable
Theoretical Background of \( \overline X \) Chart
Let \( {\overline X}_{1}, {\overline X}_{2}, ... , {\overline X}_{k} \) be the sample means obtained by selecting \(k\) samples of size \(n\), and let \( \overline {\overline X} \) be the average of these sample means. Let \( {R}_{1}, {R}_{2}, ... , {R}_{k} \) be the sample range (maximum - minimum) of each sample, and let \(\overline R\) be the average of these ranges as following: $$ \overline {\overline X} = \frac{\sum_{i=1}^{k} {\overline X}_{i} }{k} , \quad {\overline R} = \frac{\sum_{i=1}^{k} {R}_{i} }{k} $$ The mean \(\mu\) is estimated by using \( \overline {\overline X} \). Since the sample standard deviation \(s\) is not an unbiased estimator of the population standard deviation \(\sigma\), \(\sigma\) is estimated by using the mean of the ranges \(\overline R\) and the coefficient \(d_2\) that depends on the number of samples, \(n\), as follows. $$ \hat \sigma = \frac {\overline R}{d_2} $$ \(\hat \sigma\) is an unbiased estimator of the population standard deviation \(\sigma\). Here, \(d_2\) is a constant that depends on the number of samples, \(n\), and is shown in Table 6.6.1.
Table 6.6.1 Constants which are used in control charts
| sample size \(n\) |
\(A_2\) | \(D_3\) | \(D_4\) | \(d_2\) |
|---|---|---|---|---|
| 2 | 1.880 | 0 | 3.267 | 1.128 |
| 3 | 1.023 | 0 | 2.574 | 1.693 |
| 4 | 0.729 | 0 | 2.282 | 2.059 |
| 5 | 0.577 | 0 | 2.114 | 2.326 |
| 6 | 0.483 | 0 | 2.004 | 2.534 |
| 7 | 0.419 | 0.076 | 1.924 | 2.704 |
| 8 | 0.373 | 0.136 | 1.864 | 2.847 |
| 9 | 0.337 | 0.184 | 1.816 | 2.97 |
| 10 | 0.308 | 0.223 | 1.777 | 3.078 |
| 11 | 0.285 | 0.256 | 1.774 | 3.173 |
| 12 | 0.266 | 0.284 | 1.716 | 3.258 |
| 13 | 0.249 | 0.308 | 1.692 | 3.336 |
| 14 | 0.235 | 0.329 | 1.671 | 3.407 |
| 15 | 0.223 | 0.348 | 1.652 | 3.472 |
| 16 | 0.212 | 0.364 | 1.636 | 3.532 |
| 17 | 0.203 | 0.379 | 1.621 | 3.588 |
| 18 | 0.194 | 0.392 | 1.608 | 3.64 |
| 19 | 0.187 | 0.404 | 1.596 | 3.689 |
| 20 | 0.18 | 0.414 | 1.586 | 3.735 |
| 21 | 0.173 | 0.425 | 1.575 | 3.778 |
| 22 | 0.167 | 0.434 | 1.566 | 3.819 |
| 23 | 0.162 | 0.443 | 1.557 | 3.858 |
| 24 | 0.157 | 0.452 | 1.548 | 3.895 |
| 25 | 0.153 | 0.459 | 1.541 | 3.931 |
Therefore, the center line (\(CL_{\overline X}\)) and control limit lines of the \(\overline X\) chart using the estimated values of \(\mu\) and \(\sigma\) are as follows. $$ \begin{align} UCL_{\overline X} &= \overline {\overline x} + 3 \frac{\overline R / d_2}{\sqrt{n}} \\ CL_{\overline X} &= \overline {\overline x} \\ LCL_{\overline X} &= \overline {\overline x} - 3 \frac{\overline R / d_2}{\sqrt{n}} \end{align} $$ Here, by setting \( \frac{ 3 / d_2 }{\sqrt{n}} \) as a new constant \(A_2\), the control limit lines can be written as follows. The constant \(A_2\) which depends on \(n\) is also summarized in Table 6.6.1. $$ \begin{align} UCL_{\overline X} &= \overline {\overline x} + A_2 \overline R \\ CL_{\overline X} &= \overline {\overline x} \\ LCL_{\overline X} &= \overline {\overline x} - A_2 \overline R \end{align} $$
Theoretical Background of \( R\) Chart
Steps to make \(\overline X\) and \(R\) Charts
\(\overline X\) Chart: $$ \begin{align} UCL_{\overline X} &= \overline {\overline x} + A_2 \overline R \\ CL_{\overline X} &= \overline {\overline x} \\ LCL_{\overline X} &= \overline {\overline x} - A_2 \overline R \end{align} $$
\(R \) Chart: $$ \begin{align} UCL_{\overline R} &= {\overline R} D_4 \\ CL_{\overline R} &= {\overline R} \\ LCL_{\overline X} &= {\overline R} D_3 \end{align} $$
Table 6.6.2 four bolt samples were selected every hour for 25 hours from a production plant and measure the deviation from the specification 500mm
| sample | \(x_1\) | \(x_2\) | \(x_3\) | \(x_4\) | \(\overline x\) | \(R\) |
|---|---|---|---|---|---|---|
| 1 | 5 | 0 | -2 | 1 | 1.00 | 7 |
| 2 | 1 | -1 | 7 | -4 | 0.75 | 11 |
| 3 | -14 | -1 | 1 | -1 | -3.75 | 15 |
| 4 | -1 | 5 | 1 | -3 | 0.50 | 8 |
| 5 | 11 | 4 | 9 | -3 | 5.25 | 14 |
| 6 | -2 | 4 | 0 | -3 | -0.25 | 7 |
| 7 | -2 | 0 | 2 | 0 | 0.00 | 4 |
| 8 | 3 | -6 | 3 | -2 | -0.50 | 9 |
| 9 | 5 | -7 | -3 | -4 | -2.25 | 12 |
| 10 | 1 | -3 | 2 | -7 | -1.75 | 9 |
| 11 | -12 | -12 | -5 | 5 | -6.00 | 17 |
| 12 | -2 | 3 | 3 | -2 | 0.50 | 5 |
| 13 | 5 | 8 | 0 | 0 | 3.25 | 8 |
| 14 | -5 | 3 | -5 | -7 | -3.50 | 10 |
| 15 | -3 | 9 | -2 | 2 | 1.50 | 12 |
| 16 | 3 | 5 | -5 | 10 | 3.25 | 15 |
| 17 | -2 | 2 | 0 | -7 | -1.75 | 9 |
| 18 | -3 | 6 | 0 | -3 | 0.00 | 9 |
| 19 | 0 | -2 | 2 | 7 | 1.75 | 9 |
| 20 | -7 | 6 | 13 | 0 | 3.00 | 20 |
| 21 | 7 | 4 | 2 | 3 | 4.00 | 5 |
| 22 | 2 | 2 | 1 | 0 | 1.25 | 2 |
| 23 | -3 | 5 | 0 | 4 | 1.50 | 8 |
| 24 | -3 | 2 | 0 | -5 | -1.50 | 7 |
| 25 | 0 | 1 | -2 | -3 | -1.00 | 4 |
Answer
The average of 25 sample means and sample ranges are as follows. $$ \begin{align} \bar {\bar x} &= \frac { 1.0 + 0.75 + \dots +(-1.0)} {25 } = \frac{ 5.25} {25 } = 0.21 \\ \bar{R} &= \frac{7+11+ \dots +4} {25} = \frac {236} {25} = 9.44 \end{align} $$
Therefore the control limits of \(\overline X\) chart are as follows. $$ \begin{align} UCL_{\overline X} &= 0.21 + (0.729)\times(9.44) = 7.09 \\ LCL_{\overline X} &= 0.21 - (0.729)\times(9.44) = -6.67 \end{align} $$
The control limits of \(R\) chart are as follows. $$ \begin{align} UCL_{R} &= (2.282) \times (9.44) = 21.542 \\ LCL_{R} &= (0) \times (9.44) = 0 \end{align} $$
In 『eStatU』, select the menu ‘Xbar – R Control Chart’ and enter data as in <Figure 6.6.2>, then click the [Execute] button to calculate \(\overline {\overline X}\), \(\overline R\), and control limits.
<Figure 6.6.3> shows \(\overline X\) chart and \(R\) chart using sample data for 25 hours. In both control charts. No data are outside the control limits and there is no notable correlation between the data, indicating that the production process is under control during this period. Therefore, these control limit lines can be used to manage the production process for the next period.
\(\overline X\) - \(R\)
Table 6.6.3 Results of continuing sampling for next 15 hours to investigate the bolt production process. It measures the deviation from the specification 500mm
| sample | \(x_1\) | \(x_2\) | \(x_3\) | \(x_4\) | \(\overline x\) | \(R\) |
|---|---|---|---|---|---|---|
| 26 | 2 | -5 | 10 | -1 | 1.50 | 15 |
| 27 | 2 | 0 | 10 | 13 | 6.25 | 13 |
| 28 | -5 | 7 | 1 | -1 | 0.50 | 12 |
| 29 | 9 | 18 | 4 | 1 | 8.00 | 17 |
| 30 | 4 | -5 | 3 | 1 | 0.75 | 9 |
| 31 | 1 | -5 | 4 | -1 | -0.25 | 9 |
| 32 | 5 | -1 | 2 | -1 | 1.25 | 6 |
| 33 | 1 | -2 | 1 | -1 | -0.25 | 3 |
| 34 | -6 | -1 | 8 | -1 | 0.00 | 14 |
| 35 | -18 | -14 | -11 | -16 | -14.75 | 7 |
| 36 | 4 | -1 | 5 | 5 | 3.25 | 6 |
| 37 | 9 | -4 | -4 | 0 | 0.25 | 13 |
| 38 | -34 | 6 | -26 | -1 | -13.75 | 40 |
| 39 | 0 | 13 | 1 | 2 | 4.0 | 13 |
| 40 | 4 | -1 | -3 | 2 | 0.5 | 7 |
Answer
If you click the [Erase Data] button in <Figure 6.6.2>, data are erased, but both control limits are not erased as in <Figure 6.6.4>. Enter data in Table 6.6.3 and click [Execute] button to see the control charts with new data.
<Figure 6.6.5> is \(\overline X\) chart and \(R\) chart using sample data from the 26th to the 40th. The same control limits obtained in the previous example are used here. The sample means at positions 29th, 35th, and 38th in \(\overline X\) chart are out of control, and the sample range at position 38th in \(R\) chart is out of control. Any explainable cause must be identified and an appropriate action should be taken. It is necessary to analyze what factors were effected when a point exceeded the control limit lines of the control chart and eliminate the cause.
\(\overline X\) - \(R\)
6.6.2 Control Chart by Attribute
Theoretical Background of \(p\) Chart
Steps for \(p\) Chart
$$ \begin{align} UCL_{p} &= \overline p + 3 \sqrt {{\overline p}(1-{\overline p})/n } \\ CL_{p} &= \overline p \\ LCL_{p} &= \overline p - 3 \sqrt {{\overline p}(1-{\overline p})/n } \end{align} $$
Table 6.6.4 50 samples of toy cars were selected every hour for 25 hours and the number of defective products was investigated.
| sample | defectives | \(\overline p\) |
|---|---|---|
| 1 | 12 | 0.24 |
| 2 | 12 | 0.24 |
| 3 | 22 | 0.44 |
| 4 | 12 | 0.24 |
| 5 | 6 | 0.12 |
| 6 | 12 | 0.24 |
| 7 | 13 | 0.26 |
| 8 | 12 | 0.24 |
| 9 | 13 | 0.26 |
| 10 | 7 | 0.14 |
| 11 | 10 | 0.20 |
| 12 | 8 | 0.16 |
| 13 | 13 | 0.26 |
| 14 | 9 | 0.18 |
| 15 | 9 | 0.18 |
| 16 | 22 | 0.44 |
| 17 | 3 | 0.06 |
| 18 | 11 | 0.22 |
| 19 | 9 | 0.18 |
| 20 | 9 | 0.18 |
| 21 | 11 | 0.22 |
| 22 | 12 | 0.24 |
| 23 | 10 | 0.20 |
| 24 | 24 | 0.48 |
| 25 | 10 | 0.20 |
Answer
Average defective rates of total samples, \(\overline p\), is as follows. $$ \begin{align} \overline p &= \frac {\text {number of defective products in all samples} } {\text {number of products in all samples}} \\ &= \frac { 291}{50 \times 25 } = \frac { 291} {1250 } = 0.2328 \end{align} $$ Control limits of \(p\) chart are as follows. $$ \begin{align} 3 \sqrt {{\overline p}(1-{\overline p})/n } &= 3 \sqrt \frac { (0.2328)(0.7672)} { 50 } = 0.1793 \\ UCL_{p} &= 0.2328 + 0.1793 = 0.4121 \\ CL_{p} &= 0.2328 \\ LCL_{p} &= 0.2328 - 0.1793 = 0.0535 \end{align} $$ In 『eStatU』, select the menu ‘p Chart’ and enter data as in <Figure 6.6.6>, then click the [Execute] button to calculate \(\overline p\), and control limits.
<Figure 6.6.7> is the \(p\) chart using the data of Table 6.6.4. There are three points which are outside of the control limit lines in this control chart. Therefore, the process cannot be considered to be under control. In order to ensure that the process is under control, explainable causes must be found for points which are outside of contol limits.
(p)
Let us assume that the following causes have been discovered for points that are outside of the control limits. In sample number 3, the defective rate increased due to the replacement of employees with employees from other departments due to diseases, in sample number 16, it was due to paralysis of the control function of the machine, and in sample number 24, it was due to the replacement of a new machine. From these observations, exclude samples which have explainable causes and the average defective rate based on the remaining samples is calculated as follows. $$ {\overline {p}} = \frac {227} {1100} = 0.2027 $$ Control limits using the revised average defective rate are as follows. $$ \begin{align} UCL_p &= 0.2027 + 3 \sqrt { (0.2027)(0.7973)/50} = 0.2027+0.1706 = 0.3733 \\ CL_p &= 0.2027 \\ LCL_p &= 0.2027 - 0.1706 = 0.0321 \end{align} $$ <Figure 6.6.8> shows the data input after excluding three data which caused trouble. <Figure 6.6.9> is the modified \(p\) chart using new control limits after excluding points which caused trouble. None of the sample values are outside the modified control limits if the points which had an explainable cause was removed. These revised chart with new center line and limit lines will now be used as the standard for the production process.
(p)
Table 6.6.5 Fifty samples were selected every hour for the next 25 hours to investigate the number of defective products,
| sample | defectives | \(\overline p\) |
|---|---|---|
| 26 | 10 | 0.20 |
| 27 | 19 | 0.38 |
| 28 | 5 | 0.10 |
| 29 | 8 | 0.16 |
| 30 | 12 | 0.24 |
| 31 | 9 | 0.18 |
| 32 | 11 | 0.22 |
| 33 | 8 | 0.16 |
| 34 | 7 | 0.14 |
| 35 | 11 | 0.22 |
| 36 | 16 | 0.32 |
| 37 | 11 | 0.22 |
| 38 | 7 | 0.14 |
| 39 | 8 | 0.16 |
| 40 | 6 | 0.12 |
| 41 | 13 | 0.26 |
| 42 | 20 | 0.40 |
| 43 | 9 | 0.18 |
| 44 | 8 | 0.16 |
| 45 | 5 | 0.10 |
| 46 | 14 | 0.28 |
| 47 | 1 | 0.02 |
| 48 | 9 | 0.18 |
| 49 | 11 | 0.22 |
| 50 | 10 | 0.20 |
If you click the [Erase Data] button in <Figure 6.6.8>, data are erased, but the control limits are not erased as in <Figure 6.6.10> Enter data in Table 6.6.5 and click [Execute] button to see new continued charts.
<Figure 6.6.11> shows the defective rate for sample numbers 26 to 50 using the modified control limits in Example 6.6.3. It can be seen that two points are out of control limits, with two points exceeding the upper control limit and one point exceeding the lower control limit. It is necessary to look into whether there is a possible explanation for these points. In particular, points that are outside the lower control limit require more attention and investigation into the cause. This is because by investigating the cause, methods that can significantly reduce the defective rate in the production process can be researched.
(p)